Maxwell’s distribution of speeds | Chemistry Optional Notes for UPSC PDF Download
| Table of contents |

|
| The Boltzmann Distribution |

|
| Velocity distributions depend on temperature and mass |

|
| Related Speed Expressions |

|
| Solved Examples |

|
The Boltzmann Distribution
- If we were to plot the number of molecules whose velocities fall within a series of narrow ranges, we would obtain a slightly asymmetric curve known as a velocity distribution. The peak of this curve would correspond to the most probable velocity. This velocity distribution curve is known as the Maxwell-Boltzmann distribution, but is frequently referred to only by Boltzmann's name.
- The Maxwell-Boltzmann distribution law was first worked out around 1860 by the great Scottish physicist, James Clerk Maxwell (1831-1879), who is better known for discovering the laws of electromagnetic radiation. Later, the Austrian physicist Ludwig Boltzmann (1844-1906) put the relation on a sounder theoretical basis and simplified the mathematics somewhat. Boltzmann pioneered the application of statistics to the physics and thermodynamics of matter and was an ardent supporter of the atomic theory of matter at a time when it was still not accepted by many of his contemporaries.

Figure 27.3.1: Maxwell (left) and Boltzmann (right) are responsible for describing the velocity distribution of gas molecules
In section 27.2 we saw that the distribution function for molecular speeds in the x direction is given by:
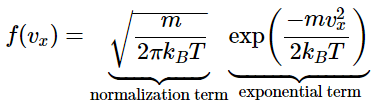
However, real gas samples have molecules not only with a distribution of molecular speeds and but also a random distribution of directions. Using normal vector magnitude properties (or simply using the Pythagorean Theorem), it can be seen that
⟨v⟩2 = ⟨vx⟩2 + ⟨vy⟩2 + ⟨vz⟩2
Since the direction of travel is random, the velocity can have any component in x, y, or z directions with equal probability. As such, the average value of the x, y, or z components of velocity should be the same. And so
⟨v⟩2 = 3⟨vx⟩2
Substituting this into the expression for pressure yields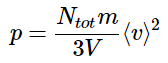
All that remains is to determine the form of the distribution of velocity magnitudes the gas molecules can take. One of the first people to address this distribution was James Clerk Maxwell (1831-1879). In his 1860 paper (Maxwell, Illustrations of the dynamical theory of gases. Part 1. On the motions and collisions of perfectly elastic spheres, 1860), proposed a form for this distribution of speeds which proved to be consistent with observed properties of gases (such as their viscosities). He derived this expression based on a transformation of coordinate system from Cartesian coordinates ( x, y, z) to spherical polar coordinates ( v, θ, ϕ). In this new coordinate system, v represents the magnitude of the velocity (or the speed) and all of the directional data is carried in the angles θ and ϕ . The infinitesimal volume unit becomes
dx dy dz = v2sin(θ) dvd θ dϕ
Applying this transformation of coordinates Maxwell’s distribution took the following form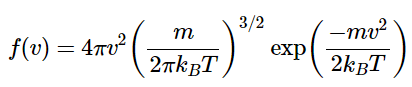 (27.3.1)
(27.3.1)
The Distribution of Speed over all Directions
The Distribution of Kinetic Energy in Three Dimensions
As noted above, the distribution function of molecular energies for one dimension is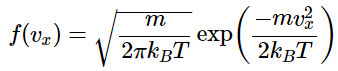 To obtain a three-dimensional probability distribution, you multiply the distribution function for each of the three dimensions so that
To obtain a three-dimensional probability distribution, you multiply the distribution function for each of the three dimensions so that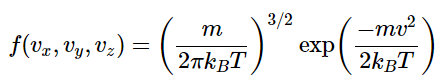 given
given
⟨v⟩2 = ⟨vx⟩2 + ⟨vy⟩2 + ⟨vz⟩2
The Conversion of Energy Distribution to Speed Distribution
To convert the three-dimensional energy distribution to a speed distribution over all space, the energy distribution must be summed over all directions. This sum is usually described by imagining a "velocity space" in spherical polar coordinates. As noted above, in this new coordinate system, v represents the magnitude of the velocity (or the speed) and all of the directional data is carried in the angles θ and ϕ. The infinitesimal volume unit becomes
dx dy dz = v2 sin(θ) dv dθ dϕ
You integrate over θ and ϕ to sum over all space, thus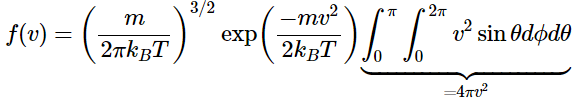
This equation is rearranged to give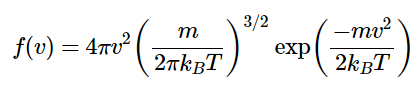
This function can be thought of as having three basic parts to it: a normalization constant (N), a velocity dependence (v2), and an exponential term that contains the kinetic energy ( ½mv2).
Because the function represents the fraction of molecules with the speed v, the sum of the fractions for all possible velocities must be unity. This sum can be calculated as an integral. The normalization constant ensures that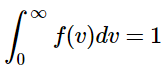
Thus the normalization constant is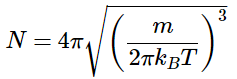
Velocity distributions depend on temperature and mass
- Higher temperatures allow a larger fraction of molecules to acquire greater amounts of kinetic energy, causing the Boltzmann plots to spread out. Figure 27.3.2 shows how the Maxwell-Boltzmann distribution is affected by temperature. At lower temperatures, the molecules have less energy.
- Therefore, the speeds of the molecules are lower and the distribution has a smaller range. As the temperature of the molecules increases, the distribution flattens out. Because the molecules have greater energy at higher temperature, the molecules are moving faster.
- Notice how the left ends of the plots are anchored at zero velocity (there will always be a few molecules that happen to be at rest.) As a consequence, the curves flatten out as the higher temperatures make additional higher-velocity states of motion more accessible. The area under each plot is the same for a constant number of molecules.
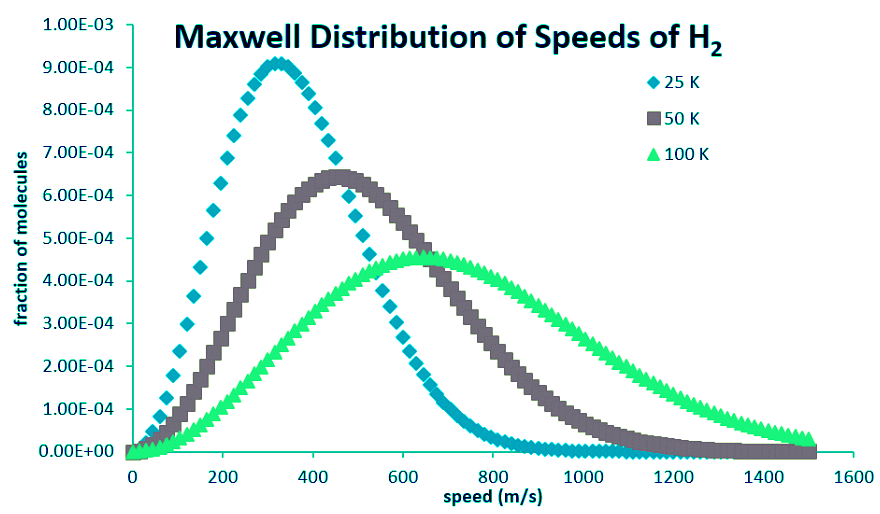
Figure 27.3.2: Maxwell Distribution of speeds for hydrogen molecules at differing temperatures.
Calculating the Average Speed
Using the Maxwell distribution as a distribution of probabilities, the average molecular speed in a sample of gas molecules can be determined.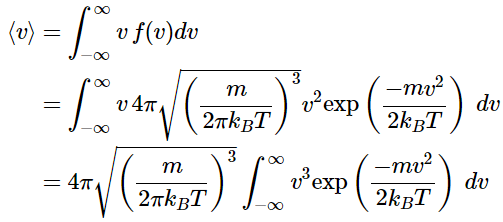
The following can be found in a table of integrals: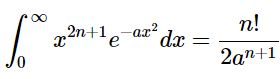
So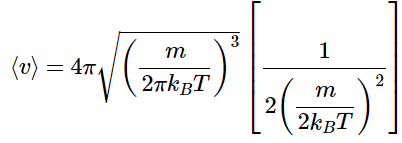
Which simplifies to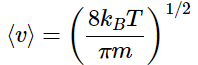
Note: the value of ⟨v⟩ is twice that of ⟨vx⟩ which was derived in an earlier example!
⟨v⟩ = 2⟨vx⟩
Solved Example
Example: What is the average value of the squared speed according to the Maxwell distribution law?
Ans: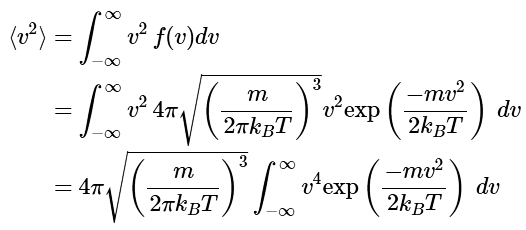
A table of integrals indicates that
Substitution (noting that n=2) yields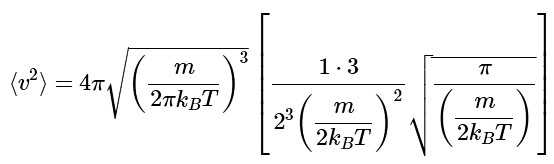
which simplifies to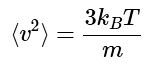
Note: The square root of this average squared speed is called the root mean square (RMS) speed, and has the value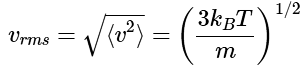
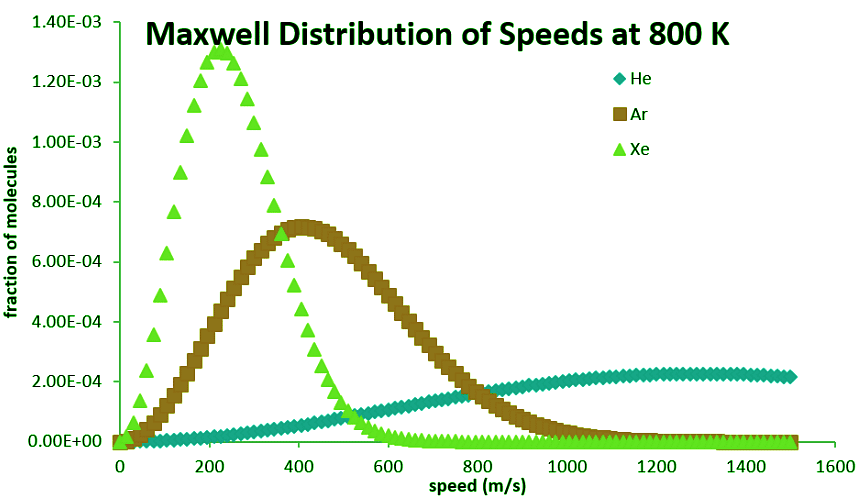
All molecules have the same kinetic energy ( ½mv2) at the same temperature, so the fraction of molecules with higher velocities will increase as m, and thus the molecular weight, decreases. Figure 27.3.3 shows the dependence of the Maxwell-Boltzmann distribution on molecule mass. On average, heavier molecules move more slowly than lighter molecules. Therefore, heavier molecules will have a smaller speed distribution, while lighter molecules will have a speed distribution that is more spread out.
Related Speed Expressions
Usually, we are more interested in the speeds of molecules rather than their component velocities. The Maxwell–Boltzmann distribution for the speed follows immediately from the distribution of the velocity vector, above. Note that the speed of an individual gas particle is:
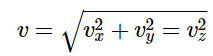
Three speed expressions can be derived from the Maxwell-Boltzmann distribution:
- the most probable speed,
- the average speed, and
- the root-mean-square speed.
The most probable speed is the maximum value on the distribution plot (Figure 27.3.4 ). This is established by finding the velocity when the derivative of Equation 27.3.1 is zero
df(v)/dv = 0
which is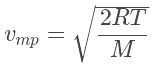 (27.3.2)
(27.3.2)
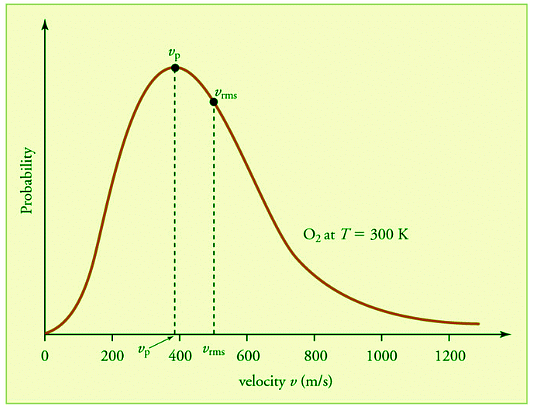 Figure 27.3.4: The Maxwell-Boltzmann distribution is shifted to higher speeds and is broadened at higher temperatures. from OpenStax. The speed at the top of the curve is called the most probable speed because the largest number of molecules have that speed.
Figure 27.3.4: The Maxwell-Boltzmann distribution is shifted to higher speeds and is broadened at higher temperatures. from OpenStax. The speed at the top of the curve is called the most probable speed because the largest number of molecules have that speed.
The average speed is the sum of the speeds of all the molecules divided by the number of molecules.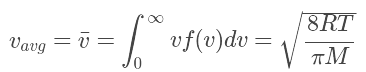 The root-mean-square speed is the square root of the average speed-squared.
The root-mean-square speed is the square root of the average speed-squared.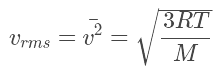
where
- R is the gas constant,
- T is the absolute temperature and
- M is the molar mass of the gas.
It always follows that for gases that follow the Maxwell-Boltzmann distribution:
vmp < vavg < vrms
Solved Examples
Example 1: Using the Maxwell-Boltzman function, calculate the fraction of argon gas molecules with a speed of 305 m/s at 500 K.
Ans: 0.00141
Example 2: If the system in problem 1 has 0.46 moles of argon gas, how many molecules have a speed of 305 m/s?
Ans: 3.92 × 1020 argon molecules
Example 3: Calculate the values of Cmp, Cavg, and Crms for xenon gas at 298 K.
Ans: cmp = 194.27 m/s, cavg = 219.21 m/s, crms = 237.93 m/s
Example 4: From the values calculated above, label the Boltzmann distribution plot with the approximate locations of Cmp, Cavg, and Crms .
Ans: As stated above, Cmp is the most probable speed, thus it will be at the top of the distribution curve. To the right of the most probable speed will be the average speed, followed by the root-mean-square speed.
Example 5: What will have a larger speed distribution, helium at 500 K or argon at 300 K? Helium at 300 K or argon at 500 K? Argon at 400 K or argon at 1000 K?
Ans: Hint: Use the related speed expressions to determine the distribution of the gas molecules: helium at 500 K. helium at 300 K. argon at 1000 K.
FAQs on Maxwell’s distribution of speeds - Chemistry Optional Notes for UPSC
| 1. What is the Boltzmann distribution? |  |
| 2. How do velocity distributions depend on temperature and mass? |  |
| 3. What is Maxwell's distribution of speeds? |  |
| 4. How can the Boltzmann distribution be applied in real-life scenarios? |  |
| 5. What are some practical implications of the Boltzmann distribution? |  |

|
Explore Courses for UPSC exam
|

|
















