Class 10 Exam > Class 10 Notes > Mathematics (Maths) Class 10 > Mind Map: Arithmetic Progressions-2
Mind Map: Arithmetic Progressions-2 | Mathematics (Maths) Class 10 PDF Download
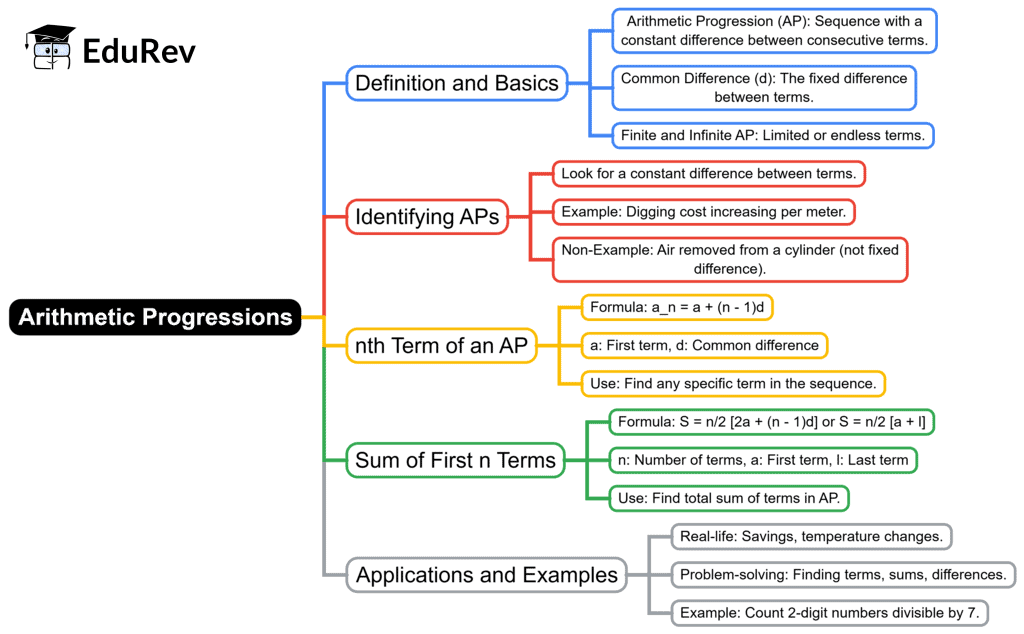
The document Mind Map: Arithmetic Progressions-2 | Mathematics (Maths) Class 10 is a part of the Class 10 Course Mathematics (Maths) Class 10.
All you need of Class 10 at this link: Class 10
|
127 videos|685 docs|84 tests
|
FAQs on Mind Map: Arithmetic Progressions-2 - Mathematics (Maths) Class 10
| 1. What is an arithmetic progression (AP)? |  |
Ans.An arithmetic progression (AP) is a sequence of numbers in which the difference between any two consecutive terms is constant. This difference is known as the common difference. For example, in the sequence 2, 5, 8, 11, the common difference is 3.
| 2. How do you find the nth term of an arithmetic progression? | |
Ans.To find the nth term of an arithmetic progression, you can use the formula: \( a_n = a + (n-1)d \), where \( a \) is the first term, \( d \) is the common difference, and \( n \) is the term number. For example, if the first term is 2 and the common difference is 3, the 5th term would be \( a_5 = 2 + (5-1)3 = 14 \).
| 3. What is the sum of the first n terms of an arithmetic progression? | |
Ans.The sum of the first n terms of an arithmetic progression can be calculated using the formula: \( S_n = \frac{n}{2} (2a + (n-1)d) \) or \( S_n = \frac{n}{2} (a + l) \), where \( l \) is the last term. For example, if the first term is 2, common difference is 3, and you want to find the sum of the first 5 terms, it would be \( S_5 = \frac{5}{2} (2 \times 2 + (5-1) \times 3) = 40 \).
| 4. Can an arithmetic progression have a negative common difference? | |
Ans.Yes, an arithmetic progression can have a negative common difference. This would result in a decreasing sequence. For example, in the sequence 10, 7, 4, 1, the common difference is -3, demonstrating a valid arithmetic progression with a negative common difference.
| 5. How do you determine if a sequence is an arithmetic progression? | |
Ans.To determine if a sequence is an arithmetic progression, you can check if the difference between consecutive terms is constant throughout the sequence. If the difference remains the same for all pairs of consecutive terms, then the sequence is an arithmetic progression. For example, for the sequence 4, 8, 12, 16, the differences (4, 4, 4) are all equal, confirming it is an AP.
About this Document
4.73/5
Rating
Sep 20, 2025
Last updated
Document Description: Mind Map: Arithmetic Progressions-2 for Class 10 2025 is part of Mathematics (Maths) Class 10 preparation.
The notes and questions for Mind Map: Arithmetic Progressions-2 have been prepared according to the Class 10 exam syllabus. Information about Mind Map: Arithmetic Progressions-2 covers topics
like and Mind Map: Arithmetic Progressions-2 Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mind Map: Arithmetic Progressions-2.
Introduction of Mind Map: Arithmetic Progressions-2 in English is available as part of our Mathematics (Maths) Class 10
for Class 10 & Mind Map: Arithmetic Progressions-2 in Hindi for Mathematics (Maths) Class 10 course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Mind Map: Arithmetic Progressions-2 | Mathematics (Maths) Class 10
Description
Full syllabus notes, lecture & questions for Mind Map: Arithmetic Progressions-2 | Mathematics (Maths) Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 10 | Best notes, free PDF download
Information about Mind Map: Arithmetic Progressions-2
In this doc you can find the meaning of Mind Map: Arithmetic Progressions-2 defined & explained in the simplest way possible. Besides explaining types of
Mind Map: Arithmetic Progressions-2 theory, EduRev gives you an ample number of questions to practice Mind Map: Arithmetic Progressions-2 tests, examples and also practice Class 10
tests
Related Searches
study material
,Semester Notes
,ppt
,Free
,Previous Year Questions with Solutions
,Objective type Questions
,Mind Map: Arithmetic Progressions-2 | Mathematics (Maths) Class 10
,Mind Map: Arithmetic Progressions-2 | Mathematics (Maths) Class 10
,video lectures
,Extra Questions
,past year papers
,shortcuts and tricks
,MCQs
,practice quizzes
,Mind Map: Arithmetic Progressions-2 | Mathematics (Maths) Class 10
,Viva Questions
,Exam
,Summary
,mock tests for examination
,Important questions
,Sample Paper
;
Additional Information about Mind Map: Arithmetic Progressions-2 for Class 10 Preparation
Mind Map: Arithmetic Progressions-2 Free PDF Download
The Mind Map: Arithmetic Progressions-2 is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Mind Map: Arithmetic Progressions-2 now and kickstart your journey towards success in the Class 10 exam.
Importance of Mind Map: Arithmetic Progressions-2
The importance of Mind Map: Arithmetic Progressions-2 cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Mind Map: Arithmetic Progressions-2 Notes
Mind Map: Arithmetic Progressions-2 Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Mind Map: Arithmetic Progressions-2.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Mind Map: Arithmetic Progressions-2 Notes on EduRev are your ultimate resource for success.
Mind Map: Arithmetic Progressions-2 Class 10 Questions
The "Mind Map: Arithmetic Progressions-2 Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Mind Map: Arithmetic Progressions-2 on the App
Students of Class 10 can study Mind Map: Arithmetic Progressions-2 alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Mind Map: Arithmetic Progressions-2,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Mind Map: Arithmetic Progressions-2 is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily