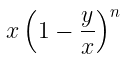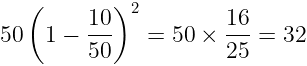Home
Explore Courses
Pricing Plans
Partner Courses
Change Class/Exams
Doubts
My Analysis
Switch to Infinity
View Analysis
Create Your Own Test
Raise a Demand
Ask a doubt
Report this question

Get the App Signup / Login

CLAT > Quantitative Techniques for CLAT > Mixture And Alligation

Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT

Table of contents
Rule of Alligation
Practice Question

1 Crore+ students have signed up on EduRev. Have you?

Mixture: The new product obtained by mixing two or more ingredients in a certain ratio is called a mixture of those particular ingredients.
Alligation: It is a method of solving arithmetic problems related to mixtures of ingredients. This rule enables us to find the ratio in which two or more ingredients at the given price must be mixed to produce a mixture of the desired price.

Rule of Alligation

Alligation is a rule that enables us to find the ratio in which two or more ingredients at the given price must be mixed to produce a mixture of the desired price.
There are two types of methods used in alligation.

(a) Alligation Method 1

The rule also helps to find out the mean or average value of mixture when the prices of two or more ingredients which may be mixed together and the ratio in which they are mixed are given.
When two ingredients at given prices are known, then the ratio in which these two are mixed to obtain a mixture of known price is given by: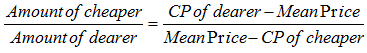 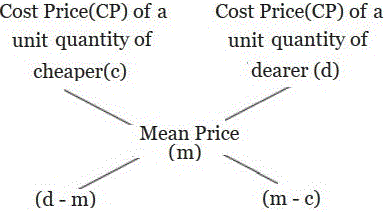Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT Hence, Amount of Cheaper: Amount of dearer = (D – M) : (M – C)

Note:
(1) This method can be used when per cent, per hour, per km, per kg etc are being compared
(2) The CP of the unit quantity of the mixture is called the mean price (M)

Example 1: In what ratio, wheat at Rs 6.20 per kg be mixed with wheat at Rs 7.20 per kg, so that the mixture is worth Rs 6.50 per kg?

Sol.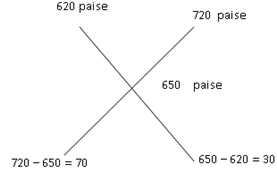 Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT Required ratio is 70 : 30 or 7 : 3

Example 2: In what ratio Rice worth Rs 30 per kg should be mixed with rice worth Rs 32.5 per kg so that on selling the mixture at Rs 34.10 per kg, the profit is 10%.

Sol. Cost price of rice so that the profit is 10% when SP is 34.10 = 34.10 x (100/110) = Rs 31

Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT

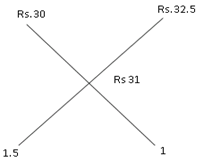
The ratio in which rice is to be mixed is 1.5:1 Or 3:2

Example 3: The mixture of a certain quantity of milk with 16 litres of water is worth 0.75 per litre. If pure milk is worth 2.25 per litre, how much milk is there in the mixture?

Sol. Cost of water is Rs 0 per litre.

Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT

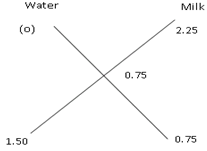
Water : Milk = 1.50 : 0.75 = 2 : 1

⇒ Quantity of milk 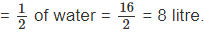Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT

(b) Alligation Method 2: Repeated Dilution

This is used to calculate pure quantity left after 'n' number of processes of repeated replacement is done on the pure quantity. Suppose, a container contains 'x' units of a liquid from which 'y' units are taken out and replaced by water.
After 'n' operations quantity of pure will be: 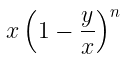Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT

Example 4: A container contains 50 litres of milk. From this container, 10 litres of milk was taken out and replaced by water. This process is repeated one more time.

How much milk is now left in the container?

Sol. Units of milk in the container, x = 50 L
Units of milk to be replaced, y = 10 L
number of process of repeated replacement = 2

Applying the Replacement Method: Amount of milk after 2 operations =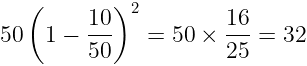 Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT

Practice Question

Question for Mixture And Alligation

Try yourself:A container contains 40 liters of milk. From this container, 4 liters of milk were taken out and replaced by water. This process was repeated further two times. How much milk is now contained by the container?

A.
26
B.
29.16
C.
28
D.
28.2

Explanation

Assume that a container contains x of liquid from which y units are taken out and replaced by water.
After n operations, the quantity of pure liquid = x(1 - y/x)ⁿ
Hence milk now contained by the container = 40(1 - 4/40)³= 40(1 - 1/10)³= 40 × 9/10 × 9/10 × 9/10 = 29.16

View Solution

Question for Mixture And Alligation

Try yourself:A vessel is filled with liquid, 3 parts of which are water and 5 parts syrup. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup?

A.
1/3
B.
1/4
C.
1/5
D.
1/7

Explanation

Suppose the vessel initially contains 8 litres of liquid.
Let x litres of this liquid be replaced with water.
Quantity of water in new mixture = (3 – 3x/8 + x) litre
Quantity of syrup in new mixture = (5 – 5x/8) litres
So (3 – 3x/8 + x) = (5 – 5x/8) litres
⇒ 5x + 24 = 40 – 5x
⇒ 10x = 16
⇒ x = 8/5 .
So, part of the mixture replaced = (8/5 x 1/8) = 1/5

View Solution

Question for Mixture And Alligation

Try yourself:Tea worth Rs. 126 per kg and Rs. 135 per kg are mixed with a third variety of tea in the ratio 1:1:2. If the mixture is worth Rs. 153 per kg, what is the price of the third variety per kg?

A.
Rs.182.50
B.
Rs.170.5
C.
Rs.175.50
D.
Rs.180

Explanation

Tea worth Rs. 126 per kg and Rs. 135 per kg are mixed in the ratio 1:1
So their average price = (126 + 135) / 2 = Rs.130.5

Hence let’s consider that the mixture is formed by mixing two varieties of tea.
one at Rs. 130.50 per kg and the other at Rs. x per kg in the ratio 2 : 2, i.e., 1 : 1.

Now let’s find out x.
By the rule of alligation, we can write as
(x – 153) : 22.5 = 1 : 1
⇒ x – 153 = 22.50
⇒ x = 153 + 22.5 = 175.5

View Solution

Question for Mixture And Alligation

Try yourself:A can contains a mixture of two liquids A and B is the ratio 7:5. When 9 liters of the mixture are drawn off and the can is filled with B, the ratio of A and B becomes 7:9. How many liters of liquid A were contained by the can initially?

A.
10
B.
20
C.
21
D.
25

Explanation

Suppose the can initially contain 7x and 5x of mixtures A and B respectively.
Quantity of A in mixture left = 7x – (7/12 x 9) = 7x – 21/4 litres.
Quantity of B in mixture left = 5x – (5/12 x 9) = 5x – 15/4 litres

(7x – 21/4) / [(5x – 15/4) +9] = 7/9
⇒ (28x – 21) / (20x + 21) = 7/9
⇒ 52x – 189 = 140x + 147
⇒ 112x = 336
⇒ x = 3.
So, the can contain 21 litres of A.

View Solution

Question for Mixture And Alligation

Try yourself:Two vessels A and B contain spirit and water in the ratio 5 : 2 and 7 : 6 respectively. Find the ratio in which these mixture be mixed to obtain a new mixture in vessel C containing spirit and water in the ration 8 : 5 ?

A.
3:4
B.
4:3
C.
9:7
D.
7:9

Explanation

Let Cost Price(CP) of the 1-litre spirit be Rs.1

Quantity of spirit in 1-litre mixture from vessel A = 5/7
Cost Price(CP) of 1 litre mixture from vessel A = Rs. 5/7
Quantity of spirit in 1 litre mixture from vessel B = 7/13
Cost Price(CP) of 1 litre mixture from vessel B = Rs. 7/13
Quantity of spirit to be obtained in 1 litre mixture from vessel C = 8/13
Cost Price(CP) of 1 litre mixture from vessel C = Rs. 8/13 = Mean Price

By the rule of alligation,
Mixture from Vessel A : Mixture from Vessel B = 1/13 : 9/91 = 7 : 9 = Required Ratio

View Solution

Question for Mixture And Alligation

Try yourself:8 litres are drawn from a cask full of wine and is then filled with water. This operation is performed three more times. The ratio of the quantity of wine now left in cask to that of the water is 16 : 65. How much wine did the cask originally hold?

A.
24 L
B.
26 L
C.
30 L
D.
32 L

Explanation

Let the initial quantity of wine = x litre
After a total of 4 operations, quantity of wine = x(1 - y/x)ⁿ= x(1 - 8/x)⁴
Given that after a total of 4 operations, the ratio of the quantity of wine left in cask to that of water = 16 : 65
Hence we can write as [x(1 - 8/x)⁴] / x = 16/81
(1-8/x)⁴ = (2/3)⁴
(1 - 8/x) = 2/3
3(x - 8) = 2x
x = 24

View Solution

Question for Mixture And Alligation

Try yourself:A dishonest milkman professes to sell his milk at cost price but he mixes it with water and thereby gains 25%. The percentage of water in the mixture is:

A.
4%
B.
20%
C.
6.25%
D.
25%

Explanation

Let C.P. of 1 litre milk be Re. 1
Then, S.P. of 1 litre of mixture = Re. 1, Gain = 25%.
C.P. of 1 litre mixture = Re.(100/125 x 1) = 4/5
By the rule of alligation,
Ratio of milk to water = 4/5 : 1/5 = 4 : 1.
Hence, percentage of water in the mixture = (1/5 x 100)% = 20%

View Solution

Question for Mixture And Alligation

Try yourself:A jar full of whiskey contains 40% alcohol. A part of this whisky is replaced by another containing 19% alcohols and now the percentage of alcohol was found to be 26%. The quantity of whisky replaced is:

A.
3/4
B.
4/3
C.
3/2
D.
1/2

Explanation

Concentration of alcohol in 1st Jar = 40%
Concentration of alcohol in 2nd Jar = 19%
After the mixing, Concentration of alcohol in the mixture = 26%
By the rule of alligation,
ratio of 1st and 2nd quantities = 7 : 14 = 1 : 2

View Solution

The document Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT is a part of the CLAT Course Quantitative Techniques for CLAT.

All you need of CLAT at this link: CLAT

	Quantitative Techniques for CLAT 56 videos\|35 docs\|91 tests

Quantitative Techniques for CLAT

56 videos|35 docs|91 tests

Join Course

Up next

	Basic Concept and Problems on Mixture and Alligation (Part - 2)
	Test: Alligation or Mixture- 1
	Test: Alligation or Mixture- 2

Top Courses for CLAT

Current Affairs & General Knowledge

Legal Reasoning for CLAT

English for CLAT

Constitution of India: Laxmikanth

Logical Reasoning for CLAT

About this Document

	2.5K Views
	4.81/5 Rating
	Gyanm Institute

Document Description: Mixture And Alligation for CLAT 2023 is part of Quantitative Techniques for CLAT preparation. The notes and questions for Mixture And Alligation have been prepared according to the CLAT exam syllabus. Information about Mixture And Alligation covers topics like Rule of Alligation, Practice Question and Mixture And Alligation Example, for CLAT 2023 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mixture And Alligation.

Introduction of Mixture And Alligation in English is available as part of our Quantitative Techniques for CLAT for CLAT & Mixture And Alligation in Hindi for Quantitative Techniques for CLAT course. Download more important topics related with notes, lectures and mock test series for CLAT Exam by signing up for free. CLAT: Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT

Description

Full syllabus notes, lecture & questions for Mixture And Alligation - Notes | Study Quantitative Techniques for CLAT - CLAT - CLAT | Plus excerises question with solution to help you revise complete syllabus for Quantitative Techniques for CLAT | Best notes, free PDF download

Information about Mixture And Alligation

In this doc you can find the meaning of Mixture And Alligation defined & explained in the simplest way possible. Besides explaining types of Mixture And Alligation theory, EduRev gives you an ample number of questions to practice Mixture And Alligation tests, examples and also practice CLAT tests