Molarity & Molality | Additional Study Material for NEET PDF Download
CONCENTRATION OF SOLUTION
Concentration of solution can be expressed in any of the following ways.
(a) % by weight:
amount of solute dissolved in 100 gm of solution.
4.9% H2SO4 by weight:
100 gm of solution contains 4.9 gm of H2SO4.
(b) % by volume:
volume of solute dissolved in 100 ml of solution.
x% H2SO4 by volume:
100 ml of solution contains x ml H2SO4
(c) % weight by volume:
wt. of solute present in 100 ml of solution.
(d) % volume by weight:
volume of solute present in 100 gm of solution.
CONCENTRATION TERMS
Molarity (M): No. of moles of solute present in 1000 ml of solution.
Molarity (M) = moles of solute/volume of solution (lit)
M = m.moles of solute/volume of solution (ml)
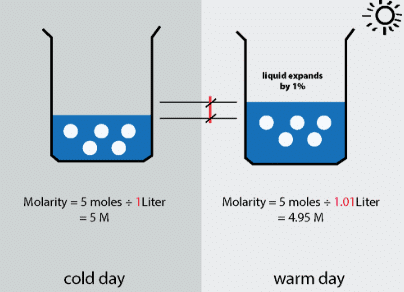 Fig: Molarity
Fig: Molarity
Molality (m): No. of moles of solute present in 1000 gm of solvent.
m = moles of solute/wt. of solvent in kg
m = m.moles of solute/wt. of solvent in gm
Normality (N):
No of gm. equivalents of solute present in 1000 ml of solution.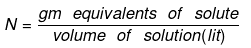
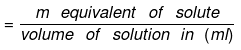
Number of gram equivalent of solute = Mass of solute in gram/equivalent weight of solute
Equivalent weight of solute (E) = Molar mass of solute/Valence factor
(i) Valence factor for base = acidity of base
(ii) Valence factor for acid = basicity of acid
(iii) Valence factor for element = valency
Thus, if one gram equivalent of a solute is present in one litre of the solution, the concentration of the solution is said to be one normal.
RELATIONSHIP BETWEEN NORMALITY AND MOLARITY
We know that,
Molarity × Molecular mass = Strength of solution (g/L)
Similarly,
Normality × Equivalent mass = Normality of the solution (g/L)
Hence,
Molarity × Molecular mass = Normality × Equivalent mass
So, Normality = n × Molarity
Formality (f): It is the number of formula mass in grams present per litre of solution. In case formula mass is equal to molecular mass, formality is equal to molarity. Like molarity and normality, the formality is also dependent on temperature. It is used for ionic compounds in which there is no existence of molecule. Mole of ionic compounds is called formole and molarity as formality.
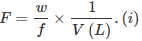
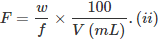
Where,
w = weight of solute,
f = formula weight of solute
V= volume of solution
nf = no. of gram formula weight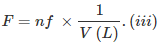
Mole fraction: The mole fraction of a particular component in a solution is defined as the number of moles of that component per mole of solution.
If a solution has nA mole of A & nB mole of B.
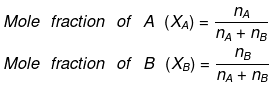
And, XA + XB = 1
Parts per million (ppm):

Volume strength of H2O2: Strength of H2O2 is represented as 10V, 20V, 30V etc.
20V H2O2 means one litre of this sample of H2O2 on decomposition gives 20 lit. of O2 gas at S.T.P.
Decomposition of H2O2 is given as: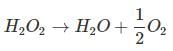

1 mole = 1/2 × 22.4 lt O2 at S.T.P.
⇒ 34 g = 11.2 lt O2 at S.T.P.
To obtain 11.2 litre O2 at S.T.P., at least 34 gm H2O2 must be decomposed, and for 20 lt O2, we should decompose at least 34/112 × 20 gm H2O2.
1 lt solution of H2O2 contains 34/112 × 20 gm H2O2
1 lt solution of H2O2 contains 34/112 × 20/17 equivalents of H2O2
(EH2O2 = M/2 = 34/2 = 17)
Normality of H2O2 = 34/112 × 20/17
Normality of H2O2 (N)
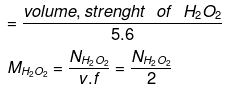
IInd Method: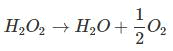
From law of equivalence:
gm eq. of O2 = gm eq. of H2O2
gm eq. of O2 = moles × n factor of O2, = 20/22.4 x 4 = 20/5.6
gm. eq. of H2O2 = 20/5.6
and the volume of H2O2 is 1 lit.
this means 1 lit of H2O2 have 20/5.6 gm eq.
i.e. Normality N = 20/5.6
Normality of H2O2 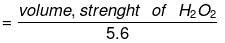
Molarity of H2O2 (M) 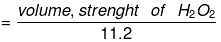
Strength (in g/l): Denoted by S.
Strength = molarity × mol. wt.
= molarity × 34
strength = Normality × Eq. weight.
= Normality × 17
Example. A bottle labeled with "12V H2O2" contain 700 ml solution. If a student mix 300 ml water in it what is the g/ liter strength & normality and volume strength o final solution.
Solution. N = 12/5.6
Meq. of H2O2 = 12/5.6 x 100
let the normality of H2O2 on dilution be N.
Meq. before dilution = Meq. after dilution
N × 1000 = 12/5.6 x 100 N = 12/5.6 × 7/10 = 1.5 M = 1.5/2
strength gm/lit = 1.5/2 x 34 = 25.5
volume strength = N × 5.6 = 8.4 V
Strength of Oleum: Oleum is SO3 dissolved in 100% H2SO4. Sometimes, oleum is reported as more than 100% by weight, say y% (where y > 100). This means that (y - 100) grams of water, when added to 100 g of given oleum sample, will combine with all the free SO3 in the oleum to give 100% sulphuric acid.
Example 1. Calculate the percentage of free SO3 in an oleum (considered as a solution of SO3 in H2SO4) that is labeled '109% H2SO4 '.
Solution.
'109% H2SO4' refers to the total mass of pure H2SO4, i.e., 109 g that will be formed when 100 g of oleum is diluted by 9 g of H2O which (H2O) combines with all the free SO3 present in oleum to form H2SO4.
H2O + SO3 → H2SO4
1 mole of H2O combines with 1 mole of SO3
or 18 g of H2O combines with 80 g of SO3
or 9 g of H2O combines with 40 g of SO3.
Thus, 100 g of oleum contains 40 g of SO3 or oleum contains 40% of free SO3.
Example 2. A 62% by mass of an aqueous solution of acid has specific gravity 1.8. This solution is diluted such that the specific gravity of solution became 1.2. Find the % by wt of acid in new solution.
Solution.
Density = 1.8
⇒ volume of solution =
Let x gm water be added in solution then
d =0.6 x = 100
⇒ x = 166.67
mass of new solution = 100 + 166.67 = 266.67
266.67 gm solution contains 62 gm of acid
% by mass = 23.24 %
Relationship between Molarity, Molality & density of solution: Let the molarity of solution be 'M', molality be 'm' and the density of solution be d gm/m.
Molarity implies that there are M moles of solute in 1000 ml of solution.
wt. of solution = density × volume
= 1000 d gm wt of solute = MM1
where M1 is the molecular wt of solute.
wt of solvent = (1000 d - MM1) gm.
(1000 d - MM1) gm of solvent contains M moles of solute.
1000 gm of solvent have
= Molality no. of moles of solute present in 1000 gm of solvent
= Molality on simplifying
Relationship between Molality & mole fraction: Consider a binary solution consisting of two components A (Solute) and B (Solvent).
Let xA & xB are the mole fraction of A & B respectively.
If molality of solution be m then
=
where MB is the molecular wt of the solvent B

Example: An aqueous solution is 1.33 molal in methanol. Determine the mole fraction of methanol & H2O.
Solution. 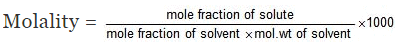
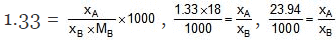
⇒ xA = 0.02394 xB, xA xB = 1
⇒ 1.02394 xB = 1
= 0.98, xA = 0.02
Second Method: Let wt. of solvent = 1000 gm, molality = 1.33
= moles of solute
mole fraction of solute =,
mole fraction of solute = 0.02
mole fraction of solvent = 1 - 0.02 = 0.98
Example. The density of 3 M solution of sodium thiosulphate (Na2S2O3) is 1.25 g/mL. Calculate
(i) amount of sodium thiosulphate
(ii) mole fraction of sodium thiosulphate
(iii) molality of Na and S2O32- ions
Solution.
(i) Let us consider one litre of sodium thiosulphate solution
wt. of the solution = density × volume (mL)
= 1.25 × 1000 = 1250 g.
wt. of Na2S2O3 present in 1 L of the solution
= molarity × mol. wt.
= 3 × 158 = 474 g.
wt. % of Na2S2O3 = 37.92%
(ii) Mass of 1 litre solution = 1.25 × 1000 g = 1250 g
[∵ density = 1.25 g/l]
Mole fraction of Na2S2O3 = Number of moles of Na2S2O3/Total number of moles
Moles of water = 1250 – 158 × 3/18 = 43.1
Mole fraction of Na2S2O3 = 3/3 + 43.1 = 0.065
(iii) 1 mole of sodium thiosulphate (Na2S2O3) yields 2 moles
of Na+ and 1 mole of S2O32-
Molality of Na2S2O3 = 3 × 1000/776 = 3.87
Molality of Na+ = 3.87 × 2 = 7.74 m
Molality of S2O2-3 = 3.87 m
|
26 videos|312 docs|64 tests
|
FAQs on Molarity & Molality - Additional Study Material for NEET
| 1. What is molarity and how is it calculated? |  |
| 2. What is the difference between molarity and molality? |  |
| 3. How is molality calculated and what is its significance? |  |
| 4. How do you convert between molarity and molality? |  |
| 5. What are some practical applications of molarity and molality in industry? |  |

















