Valence Bond Theory, Hybridization & Molecular Orbital Theory | Chemistry Class 11 - NEET PDF Download
Valence Bond Theory
- The valence bond theory was introduced by Heitler and London in 1927 and developed further by Pauling and others.
- A discussion of the valence bond theory is based on the knowledge of atomic orbitals, electronic configurations of elements, the overlap criteria of atomic orbitals, the hybridization of atomic orbitals, and the principles of variation and superposition.
To start with, let us consider the formation of a hydrogen molecule which is the simplest of all molecules:
- Consider two hydrogen atoms A and B approaching each other having nuclei NA and NB and electrons present in them are represented by eA and eB.
- When the two atoms are at a large distance from each other, there is no interaction between them.
- As these two atoms approach each other, new attractive and repulsive forces begin to operate.
- Attractive forces arise between:
(i) The nucleus of one atom and its own electron, i.e. NA – eA and NB– eB
(ii) The nucleus of one atom and electron of the other atom, i.e. NA– eB and NB– eA - Similarly, repulsive forces arise between:
(i) electrons of two atoms like eA – eB
(ii) nuclei of two atoms NA – NB - Attractive forces tend to bring the two atoms close to each other whereas repulsive forces tend to push them apart.
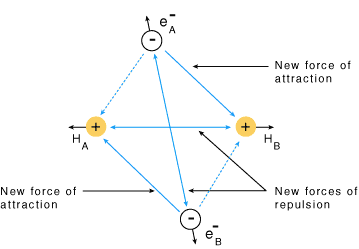 Forces of attraction and repulsion during the formation of H2 molecule
Forces of attraction and repulsion during the formation of H2 molecule - Experimentally it has been found that the magnitude of new attractive forces is more than the new repulsive forces.
- As a result, two atoms approach each other and potential energy decreases. Ultimately a stage is reached where the net force of attraction balances the force of repulsion and the system acquires minimum energy.
- At this stage, two hydrogen atoms are said to be bonded together to form a stable molecule having a bond length of 74 pm.
- Since the energy gets released when the bond is formed between two hydrogen atoms, the hydrogen molecule is more stable than that of isolated hydrogen atoms. The energy released is known as bond enthalpy, which corresponds to the minimum in the curve depicted in the graph below.
- Conversely, 435.8 kJ of energy is required to dissociate one mole of H2 molecule.
H2(g) + 435.8 kJ mol–1 → H(g) + H(g)
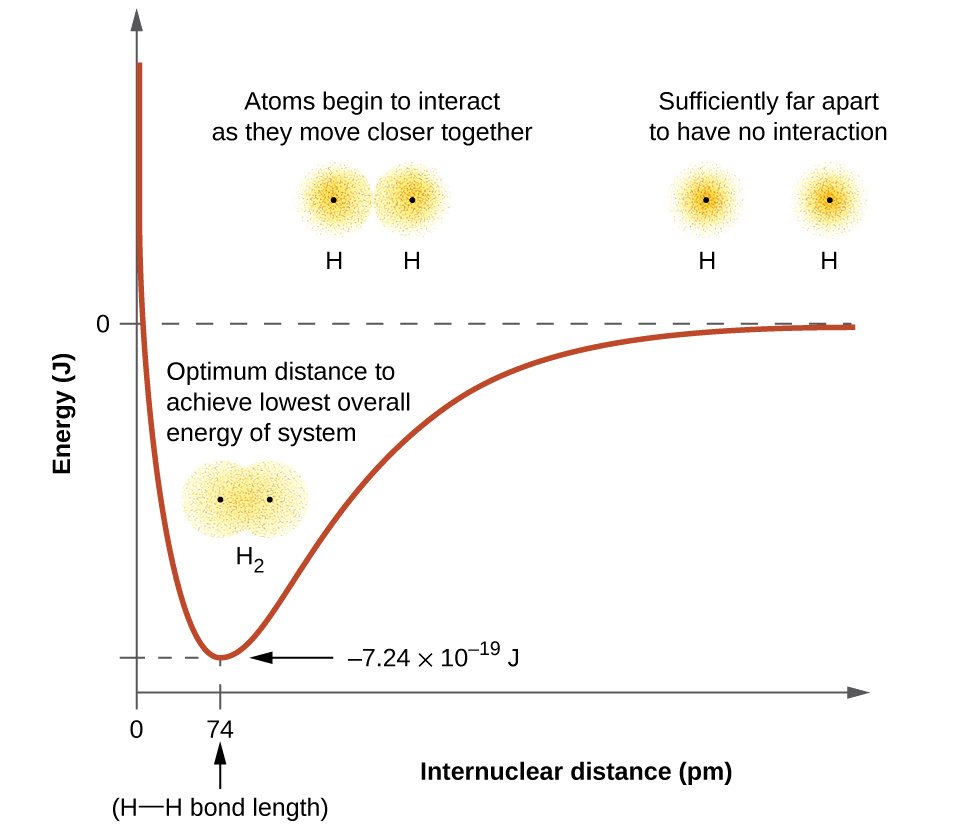 Potential energy curve for the formation of H2 molecule as a function of the internuclear distance of the H atoms
Potential energy curve for the formation of H2 molecule as a function of the internuclear distance of the H atoms
Overlapping of Atomic Orbitals
Orbital Overlap Concept
- When hydrogen molecules form, they reach a state of minimum energy when two hydrogen atoms get very close. At this point, their atomic orbitals partially merge a process called overlapping. This overlapping causes the electrons to pair up.
- The strength of the bond formed between the atoms depends on how much overlap occurs – more overlap means a stronger bond. So, according to the idea of orbital overlap, a covalent bond forms when electrons in the outer shell, with opposite spins, pair up due to this overlapping of atomic orbitals.
Overlapping of Orbitals
1. Orbital Overlap: When two atoms come close to forming a bond, the overlap of their orbitals can be positive, negative, or zero. This depends on the phase and direction of the orbital wave function in space.
2. Significance of Overlap: Positive and negative signs in diagrams indicate the phase of the orbital wave function, not charge. For a bond to form, orbitals must have the same phase and orientation in space, known as positive overlap.
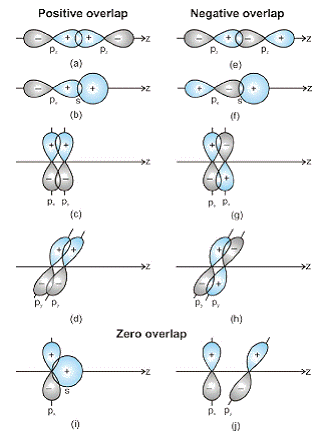 Positive, Negative, and Zero Overlap of Atomic Orbitals3. Application to Molecules: The criterion of overlap is crucial for covalent bond formation in both homonuclear/heteronuclear diatomic and polyatomic molecules.
Positive, Negative, and Zero Overlap of Atomic Orbitals3. Application to Molecules: The criterion of overlap is crucial for covalent bond formation in both homonuclear/heteronuclear diatomic and polyatomic molecules.
4. Shapes of Molecules: The shapes of CH4, NH3, and H2O molecules (tetrahedral, pyramidal, and bent, respectively) are explored using Valence Bond (VB) theory.
5. CH4 Molecule: In CH4, carbon's atomic orbitals overlap with hydrogen's 1s orbitals, forming four C-H bonds. However, the tetrahedral HCH angles of 109.5° are not explained by simple atomic orbital overlap.
6. Limitation in Explaining Bond Angles: Simple atomic orbital overlap fails to account for the directional characteristics of bonds in CH4. The 2s orbital of carbon and the 1s orbital of hydrogen can overlap in any direction.
7. Issues with NH3 and H2O Molecules: Similar arguments show that using atomic orbital overlap would predict HNH and HOH angles of 90° in NH3 and H2O, respectively, which contradicts the actual bond angles of 107° and 104.5° in these molecules.
Types of Overlapping and Nature of Covalent Bonds
Types of Covalent Bonds: Covalent bonds are classified into two types based on the types of overlapping:
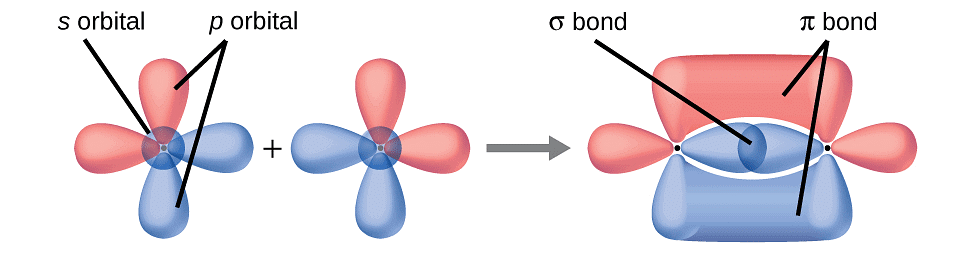
(i) Sigma (σ) Bond: Formed by end-to-end (head-on) overlap of bonding orbitals along the internuclear axis. Also known as head-on or axial overlap, it can be categorized into:
- s-s Overlapping: Overlap of two half-filled s-orbitals along the internuclear axis.
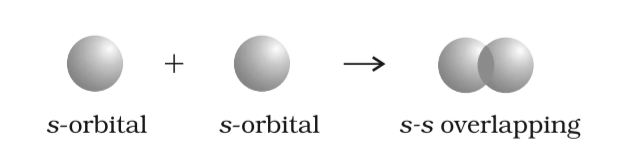 s-s Overlapping
s-s Overlapping
- s-p Overlapping: Occurs between half-filled s-orbitals of one atom and half-filled p-orbitals of another.
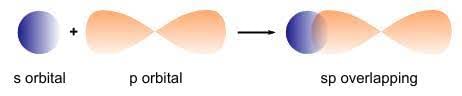 s-p Overlapping
s-p Overlapping
- p-p Overlapping: Takes place between half-filled p-orbitals of the two approaching atoms.
 p-p Overlapping
p-p Overlapping
(ii) Pi (π) Bond: Formed when atomic orbitals overlap with axes parallel to each other and perpendicular to the internuclear axis. The resulting orbitals have two saucer-type charged clouds above and below the plane of the participating atoms.
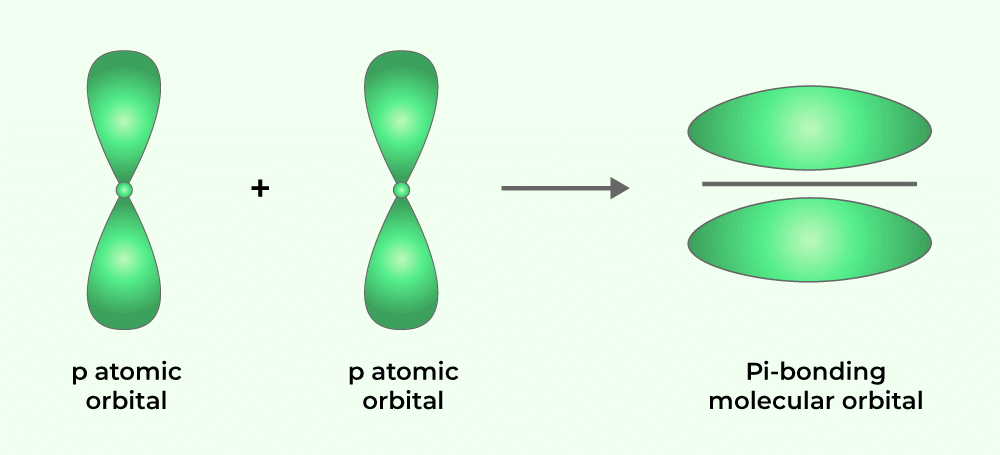 Pi Bond
Pi Bond
Strength of Sigma and Pi Bonds
- The strength of a bond depends on the extent of overlapping between atomic orbitals.
- Sigma bonds involve a larger extent of overlapping, making them stronger compared to pi bonds, where the overlapping is smaller.
- It's important to note that when two atoms in a molecule form multiple bonds, sigma bonds are always present, and in addition, pi bonds form alongside them.
What is Hybridisation?
Hybridisation is defined as the mixing of the atomic orbitals belonging to the same atom but having slightly different energies so that redistribution of energy takes place between them resulting in the formation of new orbitals of equal energies and identical shapes. The new orbitals thus formed are known as hybrid orbitals.
Some Important Points about Hybridisation
- Only those orbitals which have approximately equal energies and belong to the same atom or ion can undergo hybridisation.
- The number of hybrid orbitals produced is equal to the number of atomic orbitals mixed.
- It is not necessary that all the half-filled orbitals must participate in hybridisation. Similarly, only half-filled orbitals don't need to participate in hybridisation. Even completely filled orbitals with slightly different energies can also participate.
- Hybridisation never takes place in isolated atoms but it occurs only at the time of bond formation.
- The type of hybridisation indicates the geometry of molecules. One can tell the shape of a molecule by knowing the kind of hybridisation involved.
- The bigger lobe of the hybrid orbital always has +ve sign while the smaller lobe on the opposite side has a -ve sign.
Type of Hybridisation
1. Diagonal or sp hybridisation
- When one s and one p orbital belonging to the same main shell of an atom mix together to form two new equivalent orbitals, this type of hybridisation is called sp hybridisation or diagonal hybridisation.
- The new orbitals formed are called sp hybrid orbitals.
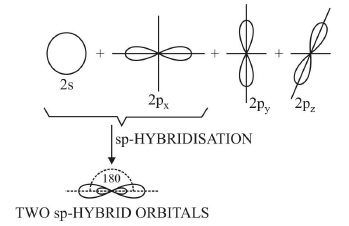 sp Hybridization
sp Hybridization
2. Trigonal or sp2 hybridisation
- When one s and two p orbitals of the same shell of an atom mix to form three new equivalent orbitals, this type of hybridisation is called sp2 hybridisation or trigonal hybridisation.
- The new orbitals formed are called sp2 hybrid orbitals.
3. sp3 – Hybridisation
In such hybridisation one s- and three p-orbitals are mixed to form four sp3– hybrid orbitals having a tetrahedral structure with bond angle 109 degrees 28′, that is, 109.5 degrees.
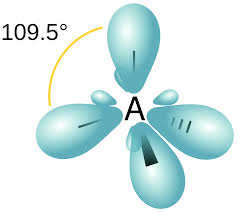
Studying the Formation of Various Molecules
1) Methane
4 equivalent C-H σ bonds can be made by the interactions of C-sp3 with an H-1s
2) Ethane
6 C-H sigma(σ) bonds are made by the interaction of C-sp3 with H-1s orbitals and 1 C-C σ bond is made by the interaction of C-sp3 with another C-sp3 orbital.
3) Formation of NH3 and H2O molecules
In the NH3 molecule nitrogen atom is sp3-hybridised and one hybrid orbital contains two electrons. Now three 1s- orbitals of three hydrogen atoms overlap with three sp3 hybrid orbitals to form NH3 molecule. The angle between H-N-H should be 109.50 but due to the presence of one occupied sp3-hybrid orbital the angle decreases to 107.80. Hence, the bond angle in NH3 molecule is 107.80.
4) Formation of C2H4 and C2H2 Molecules
In C2H4 molecule carbon atoms are sp2-hybridised and one 2p-orbital remains out to hybridisation. This forms p-bond while sp2 –hybrid orbitals form sigma- bonds.
5) Formation of NH3 and H2O Molecules by sp2 hybridization
In H2O molecule, the oxygen atom is sp3 – hybridized and has two occupied orbitals. Thus, the bond angle in the water molecule is 105.50.
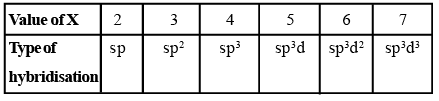
Predicting Hybridisation
Calculate the number of hybrid orbitals (X) to be formed by the central atom as follows:
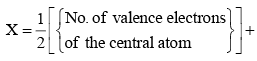
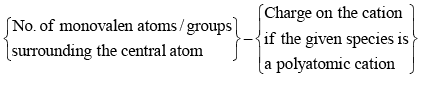
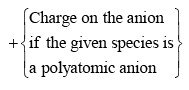
i.e. X = 1/2 [ VE + MA - c + a]
Note that only monovalent atoms (MA) or groups are to be considered. For divalent ions, MA = 0.
- If X = 2, it means two hybrid orbitals are to be formed. Hence, hybridization is sp.
- If X = 3, it means three hybrid orbitals are to be formed. Hence, hybridisation is sp2
- And so on, as given in the following table:
Molecular Orbital Theory
- The Molecular Orbital Theory (often abbreviated to MOT) is a theory on chemical bonding developed at the beginning of the twentieth century by F. Hund and R. S. Mulliken to describe the structure and properties of different molecules.
- The valence-bond theory failed to adequately explain how certain molecules contain two or more equivalent bonds whose bond orders lie between that of a single bond and that of a double bond, such as the bonds in resonance-stabilized molecules.
- The key features of the molecular orbital theory are listed below.
(I) There is Linear combination of Atomic Orbitals (LCAO) to form molecular orbitals (M.O.)
(II) The number of molecular orbitals produced is equal to the number of atomic orbitals that are combined.
(III) Two types of molecular orbitals are formed.
(a) Bonding molecular orbitals at a lower energy than the combining atomic orbitals which favour bond formation.
(b) Anti - bonding molecular orbitals at a higher energy than the combining atomic orbitals which opposes the bond formation.
Following molecular orbitals are formed when atomic orbitals overlap.
Atomic orbitals | Bonding M. O. | Anti-bonding M.O. |
1s + 1s | σ1s | σ* 1s |
2s + 2s | σ2s | σ* 2s |
2px + 2px | σ 2px | σ* 2px |
2py + 2py | π 2py | π* 2py |
2pz + 2pz | π 2pz | π* 2pz |
Electrons are filled in the increasing order of energy of the molecular orbitals which is in order of Aufbau rule
(a) When total electrons in the molecule or ions are more than 14(simple order of energy level of M. O.).
(b) When total number of electrons in the molecule are ions are ≤ 14 (modified order of energy level of M.O.).
(I) The electrons are filled in molecular orbitals in the same way as in atomic orbitals, that is, as per the Hund's Rule, Pauli exclusion principle and Aufbau rule.
(II) Number of covalent bonds between two atoms is called Bond order and is given by Bond order (B.O.) =
Where, NB = number of electrons in bonding molecular orbital and NA = number of electrons in anti bonding molecular orbitals.
(III) For a stable molecule/ion, NB > NA
(IV) A given molecule or ion is paramagnetic if it has unpaired electrons in the molecular orbital. Otherwise it is diamagnetic
(V) Greater the bond order, shorter the bond length and greater the bond energy. Thus for O2, O2 , O2—,O22-
Conditions for atomic orbitals to form M.O.
- The combining A.O. should be of comparable energy.
- The combining atomic orbitals must overlap to a large extent greater the overlap, stable is the molecule formed.
Relative energies of M.O. and filling of electron
Energy diagram is shown below:
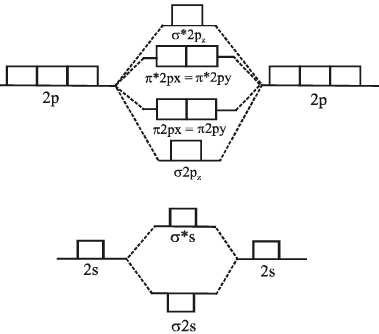 M.O Energy level diagram for O2, F2 and Ne
M.O Energy level diagram for O2, F2 and Ne
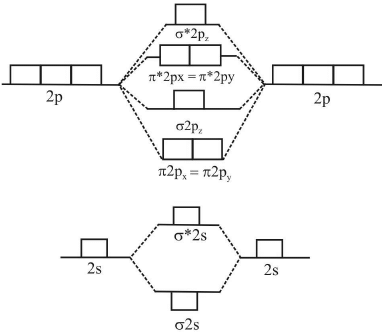 M.O energy diagram for Li2, Be2, B2, C2 and N2 molecule
M.O energy diagram for Li2, Be2, B2, C2 and N2 molecule
Crystal Field Theory
- Crystal Field Theory The drawbacks of VBT of coordination compounds are, to a considerable extent, removed by the Crystal Field Theory.
- The crystal field theory (CFT) is an electrostatic model which considers the metal-ligand bond to be ionic arising purely from electrostatic interaction between the metal ion and the ligand. Ligands are treated as point charges in case of anions or dipoles in case of neutral molecules.
- The five d-orbitals in an isolated gaseous metal atom/ion have same energy, i.e., they are degenerate. This degeneracy is maintained if a spherically symmetrical field of negative charges surrounds the metal atom/ion.
- However, when this negative field is due to ligands (either anions or the negative ends of polar molecules like NH3 and H2O) in a complex, it becomes asymmetrical and the degeneracy of the d orbitals is lost. It results in splitting of the d orbitals. The pattern of splitting depends upon the nature of the crystal field.
- In an octahedral coordination entity with six ligands surrounding the metal atom/ion, there will be repulsion between the electrons in d orbitals of metal and the electrons (or negative charges) of the ligands.
- Such a repulsion is more when the d orbitals of metal are directed towards the ligand than when it is away from the ligand.
- Thus, the 22y–x and 2zd orbitals (axial orbitals) which point towards the axis along the direction of the ligand will experience more repulsion and will be raised in energy; and the dxy, dyz and dzx orbitals (non-axial) which are directed between the axis will be lowered in energy relative to the average energy in the spherical crystal field.
- Thus, the degeneracy of the d orbitals has been removed due to ligand electron-metal electron repulsions in the octahedral complex to yield three orbitals of lower energy, t2g set and two orbitals of higher energy, eg set. This splitting of the degenerate levels due to the presence of ligands in a definite geometry is termed as crystal field splitting and the energy (CFSE) separation is denoted by Δo (the subscript o is for octahedral).

- Factors Influencing the magnitude
- Different charges on the cation of the same metal: The cation with a higher oxidation state has a larger value of CFSE than that with lower oxidation state e.g., [Fe(H2O)6]3+ > [Fe(H2O)6]2+
- Same charges on the cation but the number of d-electrons is different: The metal cation the magnitude of CFSE with the increase of the number of d-electrons, e.g., [Co(H2O)6]2+ < [Ni(H2O)6]2+
- Quantum number (n) of the d-orbitals of the central metal ion: As 'n' increases CFSE increases. [Co(NH3)6]3+ < [Rh(NH3)6]2+ < [Ir(NH3)6]3+
- Presence of cheleting ligand increases CFSE : [Fe(Ox)3]3– > [Fe(SCN)6]3–
|
114 videos|263 docs|74 tests
|
FAQs on Valence Bond Theory, Hybridization & Molecular Orbital Theory - Chemistry Class 11 - NEET
| 1. What is the concept of Valence Bond Theory in chemistry? |  |
| 2. How does overlapping of atomic orbitals contribute to the formation of covalent bonds? |  |
| 3. What is hybridization and how does it relate to Valence Bond Theory? |  |
| 4. What are the different types of overlapping and the nature of covalent bonds formed as a result? |  |
| 5. How can hybridization be predicted in molecules using Valence Bond Theory? |  |

















