NCERT Exemplar: Gravitation - 2 | Physics Class 11 - NEET PDF Download

SHORT ANSWER TYPE QUESTIONS

Q.1. Mean solar day is the time interval between two successive noon when sun passes through zenith point (meridian).
Sidereal day is the time interval between two successive transit of a distant star through the zenith point (meridian).
By drawing appropriate diagram showing earth’s spin and orbital motion, show that mean solar day is four minutes longer than the sidereal day. In other words, distant stars would rise 4 minutes early every successive day.
(Hint: you may assume circular orbit for the earth).
Ans.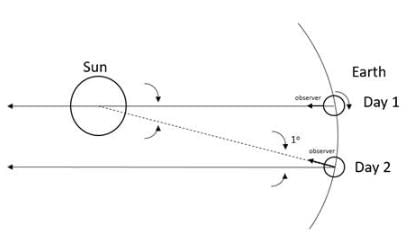

A day on earth is measured in terms of rotation of earth on its axis with respect to the sun called the mean solar day. When the day is measured with respect to a distant sun, it is called a sidereal day.
Let us look at the given figure, let the sun and distant star’s location be pointed by the long arrow at day 1, where they are directly in line with zenith of the observer on earth. When the earth rotates by 360° the arrow of the distant star points in the same direction along the zenith. However, the sun’s arrow is at an angle from the zenith. Thus, for the sun to be at the zenith in line with the observer, the earth needs to rotate an additional angle. Since the earth moves by 1° around the sun in a day, this additional angle is 1°. Now 360° is equal to 24 hours on earth or 1440 minutes, therefore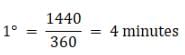

Therefore, the distant star will always rise 4 minutes earlier than the sun.

Q.2. Two identical heavy spheres are separated by a distance 10 times their radius. Will an object placed at the mid point of the line joining their centres be in stable equilibrium or unstable equilibrium? Give reason for your answer.
Ans.
Given:
Distance between centres of spheres = 10 x radius
Let the mass of the two spheres be M and their radii be R. Then, the distance between the two will be 10R. let an object of mass m be placed at the midpoint of the line joining the centres of the spheres. Then the force acting on the object due to the two spheres F₁ and F₂ will be,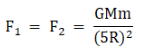

Therefore, the forces are equal and in opposite directions and therefore the mass is in stable equilibrium.
However, if the mass were to be displaced by say a distance x from the midpoint towards the sphere 2, the forces acting on the object would be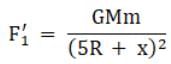


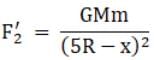
Therefore, F₂’ > F₁’ and therefore the net force acting on the mass will not be zero and equal to (F₂’ - F₁’) towards the sphere 2 and the object would be in unstable equilibrium.

Q.3. Show the nature of the following graph for a satellite orbiting the earth.
(a) KE vs orbital radius R
(b) PE vs orbital radius R
(c) TE vs orbital radius R
Ans
Given
Radius of satellite’s orbit = R
(a) Let the mass of earth be M and the mass of the satellite be m. Then the orbital velocity of the satellite will be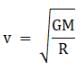

then, the kinetic energy of the satellite will be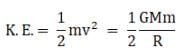

(b) the potential energy of the satellite is given by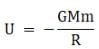 

(c) the total energy of the satellite is given by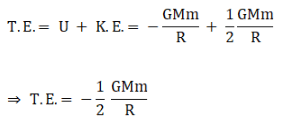

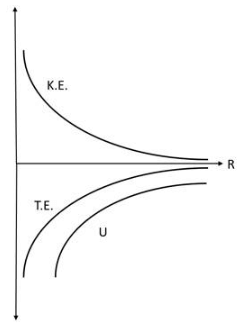
Therefore, the curves are as follows

Q.4. Shown are several curves (Figure). Explain with reason, which ones amongst them can be possible trajectories traced by a projectile (neglect air friction).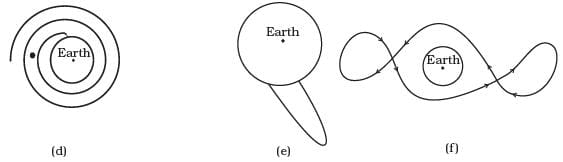


Ans. The trajectory or the path followed by a projectile under gravitational force of the earth instead of parabolic will be a conic section (for motion outside the earth) with the centre of the earth as a focus. Only the diagram in option (c) will fulfill the requirements.
Important point: In projectile we have taken the value of gravitational acceleration ‘g’ as a constant because up to some distance its variation will be neglected. The trajectory of the particle depends upon the velocity of projection. Depending upon the magnitude and direction of velocity it may be parabolic or elliptical.

Q.5. An object of mass m is raised from the surface of the earth to a height equal to the radius of the earth, that is, taken from a distance R to 2R from the centre of the earth. What is the gain in its potential energy?
Ans.
Given:
Mass of the object = m
Radius of earth = R
Initial height of the object from earth’s centre = R
Final height of the object from earth’s centre = 2R
Let the mass of earth be M. We know that the gravitational potential energy of an object is given by,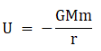

Where r is the distance between the object and centre of earth. When the object is at its initial position it is at a distance of R from the centre of the earth. Then its potential energy,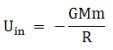

When the object is raised to a height 2R, then the potential energy is given by,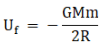

Now the gain in gravitational potential energy is given by


Q.6. A mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r (Figure).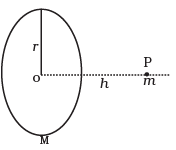

If the mass is removed further away such that OP becomes 2h, by what factor the force of gravitation will decrease, if h = r?
Ans.
Given:
Mass of the ring = M
Layout of the ring = r
Mass of the object = m
Initial distance of the object h = r
Final distance of the object 2h = 2r
To find the gravitational force on the object of mass m due to the ring let us consider an elemental mass on the ring of mass dM. The force due to this elemental mass is then,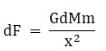


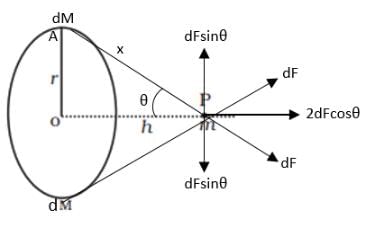
where x is the distance of the object from the elemental mass m and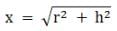

Now at the point P the force dF can be resolved into a vertical component and a horizontal component. If we consider two elemental masses diametrically opposite to each other, then the vertical component due to the two forces cancel each other as they are equal and opposite and the horizontal forces add up. Therefore, we only need to consider the horizontal component of the forces, therefore the net force on the object,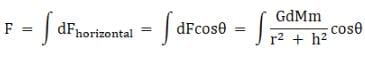

Now from the triangle OPA in the figure we have,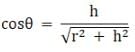 

therefore,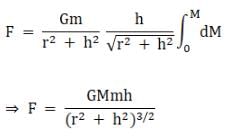 

When h = r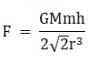

When h = 2h = 2r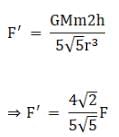

Therefore, the force decreases by a factor of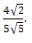  

LONG ANSWER TYPE QUESTIONS

Q.1. A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum l. As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease.
Ans. 
Given:
Radius of the orbit of planets = r
Let the mass of the sun be M and the planet be m.
(a) The force on an object revolving around the star is given by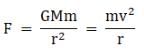


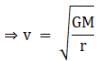
Therefore, linear velocity v is inversely proportional to square root of r and hence when r increases, v decreases.
(b) The angular velocity ω is given by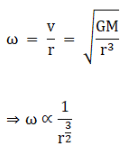

Therefore, when r increases, ω decreases.
(c) The kinetic energy K is given by,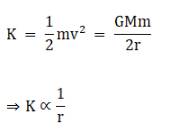

Therefore, as r increases, K decreases.
(d) The potential energy U is given by,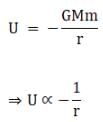

Therefore, as r increases U becomes less negative or increases.
(e) The total energy E is given by,

Therefore, as r increases E becomes less negative or increases.
(f) The angular momentum L is given by,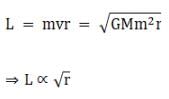

Therefore, as r increases, L increases.

Q.2. Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
Ans.
Given
Side of hexagon = l
The force on the masses will be the resultant of the forces of all the other masses. Let the masses be m each. Now the distance AC is given by the parallelogram law i.e.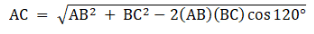


Due to symmetry we have AC = AE = 1√3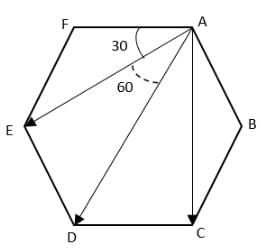

Now, for AD we have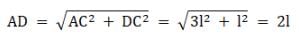

Now the force on mass at A due to b is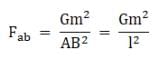

Also
F_ab = F_at
The force on mass A due to C is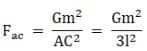

Also due to symmetry, we have
F_ac = F_ae
The force on mass at A due to mass at D is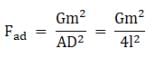

Now, the forces F_ae and F_ac make equal angles with the direction AD viz. 30°, and therefore by parallelogram law of vector addition their resultant is along AD and therefore the magnitude of the resultant,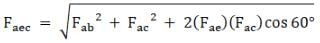


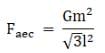
Similarly, F_ab and F_af also make equal angles with AD viz. 60° and therefore they are also along AD and


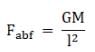
Therefore, the net force on mass at A will be
F = F_aec + F_abf + F_ad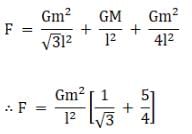


Q.3. A satellite is to be placed in equatorial geostationary orbit around earth for communication.
(a) Calculate height of such a satellite.
(b) Find out the minimum number of satellites that are needed to cover entire earth so that at least one satellites is visible from any point on the equator.
[M = 6 × 10²⁴ kg, R = 6400 km, T = 24h, G = 6.67 × 10^–11 SI units]
Ans. 
(a) For a geostationary satellite, the centripetal force must equal the gravitational force. Let the mass of earth be M and the satellite be m, then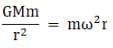

Where r is the radius of the orbit of the satellite and ω is its angular velocity
ω = 2π/T
where T is the time period of revolution, then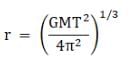

Now the height h of the satellite from the surface of the earth,
h = r - R
where R is the radius of earth.
For a geostationary satellite, the time period is 24 hours or 86400 seconds,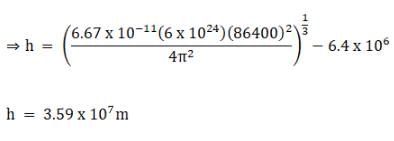

(b) A geostationary satellite is visible form the equator in the region shown in the figure having an angle 2θ,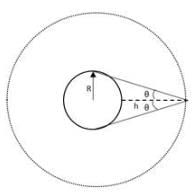

Now from the figure we have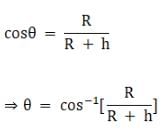

θ = cos^-1[0.152] = 81.29⁰
Now 2θ = 162.58, therefore to cover the earth with such satellites so that from any point on the equator a satellite can be seen,
360/162.58 = 2.21 ≈ 3

Q.4. Earth’s orbit is an ellipse with eccentricity 0.0167. Thus, earth’s distance from the sun and speed as it moves around the sun varies from day to day. This means that the length of the solar day is not constant through the year. Assume that earth’s spin axis is normal to its orbital plane and find out the length of the shortest and the longest day. A day should be taken from noon to noon. Does this explain variation of length of the day during the year?
Ans.
Given
The eccentricity of earth’s orbit e = 0.0167
Let the earth - sun distance at the aphelion and perihelion be r_a and r_p respectively, and the angular velocity at those points be ω_a and ω_p. Now since the angular momentum of the earth is conserved we have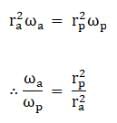

Now, from the ellipse we have
r_p = a(1-e) and r_a = a(a+e)
Where a is the semi - major axis of the ellipse

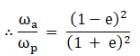
Since e = 0.0167
⇒ ω_a/ω_p = 1.069
And since the mean angular velocity is the geometric mean of the two, we have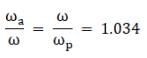

Now we know that the mean solar day corresponds to 1° on the orbit of earth. A mean solar day has 24 h for which the earth rotates 361°. Thus for aphelion the earth rotates 361.034° and hence the time for the day is 24 hours and 8.1 seconds, and the for the perihelion the earth rotates 359.96° and the time is 23 hours and 52 seconds. Thus the longest day is 8.1 seconds long and the shortest day is 8 seconds shorter. However, the variation of length of day in the year is not explained by this phenomenon as the total time of the day still remains around 24 hours, while the amount of time the sun is visible changes.

Q.5. A satellite is in an elliptic orbit around the earth with aphelion of 6R and perihelion of 2 R where R= 6400 km is the radius of the earth. Find eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius 6R ?
[G = 6.67 × 10^–11 SI units and M = 6 × 10²⁴ kg]
Ans.
Given
Radius of earth = R = 6400 km
Aphelion earth - satellite distance r_a = 6R
Perihelion earth - satellite distance r_p = 2R
We know for an ellipse
r_p = a(1-e) and r_a = a(1+e)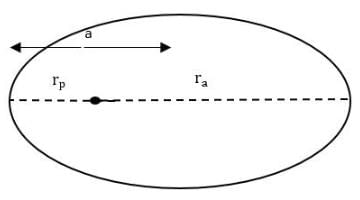

Where e is the eccentricity of the ellipse, and the semi major axis.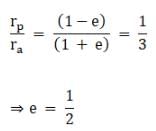

Now, the angular momentum of the satellite is conserved we then, we have
mr_pv_p=mr_av_a
Where m is the mass of satellite and v_p and v_a are the velocities at the perigee and apogee respectively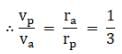

Now from conservation of energy at the apogee and perigee
K_P + U_P = K_a + U_a
Where K and U are the kinetic and gravitational potential energy of the satellite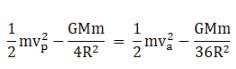

Where M is the mass of earth. Using the relation between v_p and v_a above we have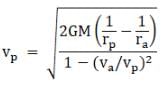

Putting the values of r_p and r_a we have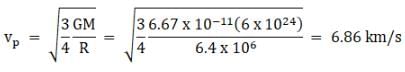

∴ v_a = v_P/3 = 2.29 km/s
To transfer the satellite to a circular orbit of radius 6R the satellite’s velocity has to be maintained at a value of