NCERT Exemplar: Gravitation | Physics Class 11 - NEET PDF Download
MULTIPLE CHOICE QUESTION I
Q1: The earth is an approximate sphere. If the interior contained matter which is not of the same density everywhere, then on the surface of the earth, the acceleration due to gravity
(a) Will be directed towards the centre but not the same everywhere.
(b) Will have the same value everywhere but not directed towards the centre.
(c) Will be same everywhere in magnitude directed towards the centre.
(d) Cannot be zero at any point.
 View Answer
View Answer 
Ans: (d)
If the density of the earth is non-uniform then ‘g’ at different point on the surface of the earth will be different.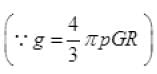
If we substitute any value of density, g ≠ 0 at any point.
Q2: As observed from earth, the sun appears to move in an approximate circular orbit. For the motion of another planet like mercury as observed from earth, this would
(a) Be similarly true.
(b) Not be true because the force between earth and mercury is not inverse square law.
(c) Not be true because the major gravitational force on mercury is due to sun.
(d) Not be true because mercury is influenced by forces other than gravitational forces.
 View Answer
View Answer 
Ans: (c)
Force of attraction between any two objects obeys the inverse square law as its universal law. The relative motion between Earth, Mercury as observed from Earth will not be circular as the force on Mercury due to the sun is very large than due to Earth and due to the relative motion of Sun and Earth with Mercury.
Q3: Different points in earth are at slightly different distances from the sun and hence experience different forces due to gravitation.
For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the c.m. (centre of mass) causing translation and a net torque at the c.m. causing rotation around an axis through the c.m.
For the earth-sun system (approximating the earth as a uniform density sphere)
(a) The torque is zero.
(b) The torque causes the earth to spin.
(c) The rigid body result is not applicable since the earth is not even approximately a rigid body.
(d) The torque causes the earth to move around the sun.
 View Answer
View Answer 
Ans: (a)
The torque on earth due to gravitational attractive force on earth is zero, because the direction of force (F) (gravitational) and the line joining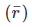 , the point of application of force (which also is at c.m. of earth) is along the same direction, so angle between
, the point of application of force (which also is at c.m. of earth) is along the same direction, so angle between 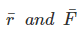 is zero or
is zero or 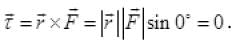
Q4: Satellites orbiting the earth have finite life and sometimes debris of satellites fall to the earth. This is because,
(a) The solar cells and batteries in satellites run out.
(b) The laws of gravitation predict a trajectory spiralling inwards.
(c) Of viscous forces causing the speed of satellite and hence height to gradually decrease.
(d) Of collisions with other satellites.
 View Answer
View Answer 
Ans: (c)
We know that the total energy of the earth satellite of radius R bounded system is negative
(-GM\ 2 R)
where M is mass of the earth. –
Due to the atmospheric friction (viscous force) acting on satellite, energy decreases continuously, radius of the orbit or height decreases gradually and the satellite spirals down with increasing speed till it bums in the denser layers of the atmosphere.
Q5: Both earth and moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon
(a) Will be elliptical.
(b) Will not be strictly elliptical because the total gravitational force on it is not central.
(c) Is not elliptical but will necessarily be a closed curve.
(d) Deviates considerably from being elliptical due to influence of planets other than earth.
 View Answer
View Answer 
Ans: (b)
Moon revolves around the earth in a nearly circular orbit. When it is observed from the sun, two types of forces are acting on the moon one is due to gravitational attraction between the sun and the moon and the other is due to gravitational attraction between the earth and the moon. So moon is moving under the combined gravitational pull acting on it due to the earth and the sun. Hence, total force on the moon is not central.
Q6: In our solar system, the inter-planetary region has chunks of matter (much smaller in size compared to planets) called asteroids. They
(a) Will not move around the sun since they have very small masses compared to sun.
(b) Will move in an irregular way because of their small masses and will drift away into outer space.
(c) Will move around the sun in closed orbits but not obey Kepler’s laws.
(d) Will move in orbits like planets and obey Kepler’s laws.
 View Answer
View Answer 
Ans: (d)
Like any other planet, asteroids also follow Kepler’s law and move in elliptical orbits around planet due to the central gravitational force acting on them.
small mass of asteroid does not escape the gravitational force due to sun because of large mass of sun and hence, (a) is incorrect. Since gravitational force follow inverse square law, the asteroid will move in circular or elliptical orbits and (b) is incorrect option
Q7: Choose the wrong option.
(a) Inertial mass is a measure of difficulty of accelerating a body by an external force whereas the gravitational mass is relevant in determining the gravitational force on it by an external mass.
(b) That the gravitational mass and inertial mass are equal is an experimental result.
(c) That the acceleration due to gravity on earth is the same for all bodies is due to the equality of gravitational mass and inertial mass.
(d) Gravitational mass of a particle like proton can depend on the presence of neighbouring heavy objects but the inertial mass cannot.
 View Answer
View Answer 
Ans: (d)
Inertial mass:
The mass of an object A can be defined as the mass of the object obtained by measuring their accelerations under equal forces taking mass of B to be 1kg. This is known as inertial mass.
Gravitational mass:
The gravitational force exerted by a massive body on an object is proportional to the mass of the object. If FA and FB are the forces of attraction on the two objects due to the earth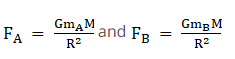
Thus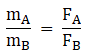
If B is a standard unit mass, by measuring gravitational Force we can obtain the mass of object A which is known as gravitational mass.
By several experiments, it has been concluded that the inertial and gravitational mass are identical.
Q8: Particles of masses 2M, m and M are respectively at points A, B and C with AB = ½ (BC). m is much-much smaller than M and at time t = 0, they are all at rest (Figure).
At subsequent times before any collision takes place: (a) m will remain at rest
(a) m will remain at rest
(b) m will move towards M
(c) m will move towards 2M
(d) m will have oscillatory motion
 View Answer
View Answer 
Ans: (c)
Let FBC be the force experienced by mass m at point B due to mass M at point C, and FBA be the force experienced by mass m at point B due to mass 2M at point A.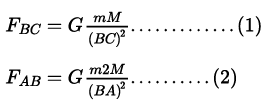
Suppose AB = x, then 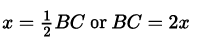
Substituting the values of AB and BC in the above equations (1) and (2)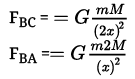
As FBA > FBC, m will move towards point A (position of particle with mass 2M).
MULTIPLE CHOICE QUESTIONS II
Q9: Which of the following options are correct?
(a) Acceleration due to gravity decreases with increasing altitude.
(b) Acceleration due to gravity increases with increasing depth (assume the earth to be a sphere of uniform density).
(c) Acceleration due to gravity increases with increasing latitude.
(d) Acceleration due to gravity is independent of the mass of the earth
 View Answer
View Answer 
Ans: (a, c)
(a) The acceleration due to gravity at an altitude (height), 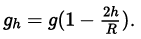
increasing height (h) decreases the value of gh. option (a) is correct.
(b) Assuming the earth to be a sphere of uniform density, the acceleration due to gravity at a particular depth (d) 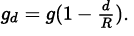
Increasing depth (d) decreases the value of gd. Option (b) is incorrect.
(c) If λ is latitude on earth then gλ = g - ω2R cos2 λ
As value of cos λ decrease from 0º to 90º ( from 1 to 0). The acceleration due to gravity increases from equator (λ = 0º) to pole (λ = 90º). Option (c) is correct.
(d) The acceleration due to gravity on surface of earth is 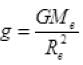
So g on earth depends on mass of earth. Option (d) is incorrect.
Q10: If the law of gravitation, instead of being inverse-square law, becomes an inverse-cube law
(a) planets will not have elliptic orbits.
(b) circular orbits of planets is not possible.
(c) projectile motion of a stone thrown by hand on the surface of the earth will be approximately parabolic.
(d) there will be no gravitational force inside a spherical shell of uniform density.
 View Answer
View Answer 
Ans: (a, b, c)
If the law of gravitation becomes an inverse cube law instead of inverse square law, then for a planet of mass m revolving around the sun of mass M, we can write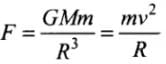 (where R is the radius of orbiting planet)
(where R is the radius of orbiting planet)
⇒ Orbital Speed 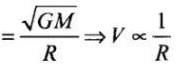
Time period of revolution of a planet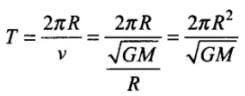
⇒ T2 ∝ R4
Hence, orbit will not be elliptical.
[for elliptical orbit T2 ∝ R3]
The circular orbits of the planets is not possible according to new law of gravitation.
As force 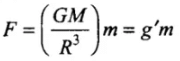
where, 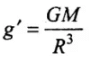
As g' acceleration due to gravity is constant, hence path followed by a projectile will be approximately parabolic, (as T ∝ R2).
Also, gravitational force inside a spherical shell of uniform density will have some value. So, only option (d) is incorrect.
Q11: If the mass of sun were ten times smaller and gravitational constant G were ten times larger in magnitudes
(a) Walking on ground would became more difficult.
(b) The acceleration due to gravity on earth will not change.
(c) Raindrops will fall much faster.
(d) Airplanes will have to travel much faster
 View Answer
View Answer 
Ans: (a, c, d)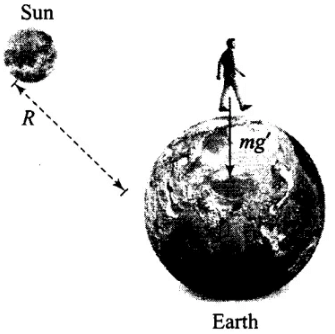 According to the problem
According to the problem
G' = 10G
From the adjacent diagram
Gravitational field due to the earth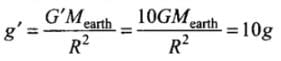
Weight of person = mg' = m x 10 g = 10 mg
force on the man due to the sun 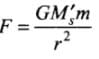
As r »R (radius of the earth)
⇒ F will be very small.
So, the effect of the sun will be neglected.
Due to this reason gravity pull on the person will increase. Due to it, walking on ground would become more difficult.
Critical velocity, vc is proportional to g, i.e., vcg
As, g’ > g => vc‘>vc
Hence, rain drops will fall much faster.
To overcome the increased gravitational force of the earth, the aeroplanes will have to travel much faster.
Q12: If the sun and the planets carried huge amounts of opposite charges,
(a) All three of Kepler’s laws would still be valid
(b) Only the third law will be valid
(c) The second law will not change
(d) The first law will still be valid
 View Answer
View Answer 
Ans: (a, c, d)
Coulomb’s electric force or Electrostatic force of attraction will produce due to opposite charges.
If the sun and the planets carries huge amount of opposite charges, then electrostatic force of attraction will be large. Gravitational force is also attractive in nature have both forces will be added and both are radial in nature.
Both the forces obey inverse square law and are central forces. As both the forces are of same nature, hence all the three Kepler’s laws will be valid.
Q13: There have been suggestions that the value of the gravitational constant G becomes smaller when considered over very large time period (in billions of years) in the future. If that happens, for our earth,
(a) Nothing will change
(b) We will become hotter after billions of years
(c) We will be going around but not strictly in closed orbits
(d) After sufficiently long time we will leave the solar system
 View Answer
View Answer 
Ans: (c, d)
We know that gravitational force exists between the earth and the sun.
FG = G(MS x me)/ r2
Where MS is mass of the sun and me is mass of the earth.
This provides the necessary centripetal force for the circular orbit of the earth around the sun. As G decreases with time, the gravitational force FG will become weaker with time. As FG is changing with time due to it, the earth will be going around the sun not strictly in closed orbit and radius also increases, since the attraction force is getting weaker.
Hence, after long time the earth will leave the solar system.
Q14: Supposing Newton’s law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read 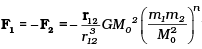 where M0 is a constant of dimension of mass, r12 = r1 –r2 and n is a number. In such a case,
where M0 is a constant of dimension of mass, r12 = r1 –r2 and n is a number. In such a case,
(a) The acceleration due to gravity on earth will be different for different objects
(b) None of the three laws of Kepler will be valid
(c) Only the third law will become invalid
(d) For n negative, an object lighter than water will sink in water
 View Answer
View Answer 
Ans: (a, c, d)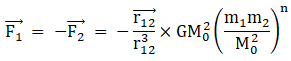
Where Mo = constant
For calculating acceleration due to gravity let
M1 = Mass of earth = M
M2 = mass of object
r12 = radius of earth = R
Then magnitude of force between the object and earth is given by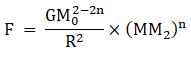
Which can be said as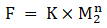
Where K is a constant
Therefore, acceleration due to gravity can be calculated as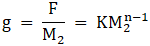
Which depends on mass and hence different for different objects
Therefore (a) is the correct option
since this force follows inverse square law, hence Kepler’s first two are valid but since g is no longer constant, therefore Kepler’s third law (Law of periods) does not remain valid therefore (c) is the correct option
when n is negative than force is given by
Where a = - n
Therefore, force is inversely proportional to mass of body, hence an object lighter than water will experience more force than water and therefore will sink in water
Therefore (a), (c) and (d) are the correct options
Q15: Which of the following are true?
(a) A polar satellite goes around the earth’s pole in north south direction
(b) A geostationary satellite goes around the earth in east-west direction
(c) A geostationary satellite goes around the earth in west-east direction
(d) A polar satellite goes around the earth in east-west direction
 View Answer
View Answer 
Ans: (a, c)
The satellite which appears stationary relative to earth is called the geostationary satellite. It revolves around the earth in the west-east direction with the same angular velocity as done by the earth about its own axis in the west-east direction. A polar satellite revolves around the earth's pole in north-south direction. It is independent of earth's rotation. Option (a), (c) are correct.
Q16: The centre of mass of an extended body on the surface of the earth and its centre of gravity
(a) Are always at the same point for any size of the body
(b) Are always at the same point only for spherical bodies
(c) Can never be at the same point
(d) Is close to each other for objects, say of sizes less than 100 m
(e) Both can change if the object is taken deep inside the earth
 View Answer
View Answer 
Ans: (d)
The center of gravity is based on weight, whereas the center of mass is based on mass. So, when the gravitational field across an object is uniform, the two are identical. However, when the object enters a spatially-varying gravitational field, the COG will move closer to regions of the object in a stronger field, whereas the COM is unmoved.
More practically, the COG is the point over which the object can be perfectly balanced; the net torque due to gravity about that point is zero. In contrast, the COM is the average location of the mass distribution or it is the point where whole mass of the body is supposed to be concentrated. If the object were given some angular momentum, it would spin about the COM.
For small objects, say of sizes less than 100 m placed in uniform gravitational field then centre of mass is very close with the centre of gravity of the body. But when the size of object increases, its weight changes and its CM and CG become far from each other. Like in the case of spherical ball, the CM and the CG are the same, but in case of Mount Everest, its CM lies a bit above its CG.
VERY SHORT ANSWER TYPE QUESTIONS
Q1: Molecules in air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.
 View Answer
View Answer 
Ans: Air molecules in the atmosphere are attracted by gravitational force of the earth but they do not fall into earth due to the reason that the molecules in air has some random motion due to temperature, so their resultant motion is not exactly in the vertical downward direction.
But in case of apple, only vertical motion dominates because of being heavier than air molecules. But due to gravity, the density of air is more near to the earth than the density as we go up.
Q2: Give one example each of central force and non-central force.
 View Answer
View Answer 
Ans:
Examples of central force:
(i) Gravitational force due to point mass.
(ii) Electrostatic force on the point charge.
Examples of non-central force:
(i) Nuclear force which depends upon the spin of particles.
(ii) Magnetic systems acting between two current carrying loops
Q3: Draw areal velocity versus time graph for mars.
 View Answer
View Answer 
Ans: Areal velocity of Mars revolving around the Sun does not change with time according to Kepler’s law, i.e. it is constant with time. Then graph of a real velocity versus time is a straight line parallel to time axis.
Q4: What is the direction of areal velocity of the earth around the sun?
 View Answer
View Answer 
Ans: Areal velocity of the earth around the sun is given by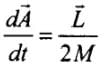
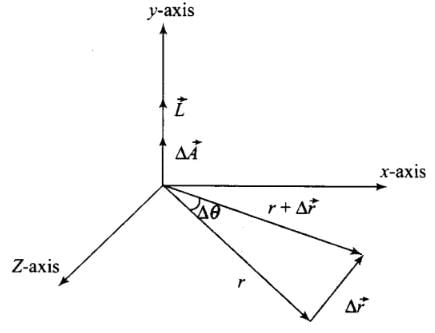
where, L is the angular momentum and M is the mass of the earth.
But angular momentum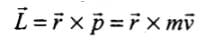
Therefore we get,
∴ 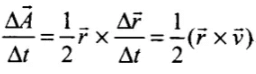
Therefore, the direction of a real velocity 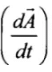 is in the direction of
is in the direction of 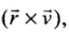
i.e., perpendicular to the plane containing r and v and directed as given by right hand rule. So, areal velocity is normal to the plane containing Earth and Sun as shown in the figure
Q5: How is the gravitational force between two point masses affected when they are dipped in water keeping the separation between them the same?
 View Answer
View Answer 
Ans: Gravitational force acting between two point masses m1 and m2 is given by the relation,
F = G m1m2/ r2
It does not depend upon the medium separating the two point masses. Therefore, gravitational force acting between two point masses will remain unaffected when they are dipped in water keeping the separation between them same. Only their apparent weights change, there is no effect on masses.
Q6: Is it possible for a body to have inertia but no weight?
 View Answer
View Answer 
Ans: Yes, a body can have inertia but no weight. Inertia of a body is related to mass. Where as weight of body is defined as
W = mg
Where
M = mass of body
g = acceleration due to gravity
therefore, weight of the object can be zero when the acceleration due to gravity becomes zero.
Since we know that at the centre of earth, the value of acceleration due to gravity is zero and hence the weight of the object is zero at the centre, but it remains mass(inertia) remains constant.
Q7: We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
 View Answer
View Answer 
Ans: The gravitational force does not depend upon the nature of the medium, but the electric force depends on the intervening medium between the charge and the electric field. So we cannot shield a body from the gravitational force.
Q8: An astronaut inside a small spaceship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?
 View Answer
View Answer 
Ans: Astronaut inside a small spaceship experience a very small negligible constant acceleration and hence astronaut feel weightlessness. If the space station has too much large mass and size then he can only experience acceleration due to gravity in the proximity of moon or on the moon.
Q9: The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
 View Answer
View Answer 
Ans:
Given:
Radius of hollow shell = R
Distance of point mass from centre of hollow shell = r
Let the mass of the spherical shell be M and the point mass be m. Then the force between the shell and the point mass is given by,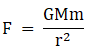
When point mass is positioned such that it is inside the hollow sphere i.e. 0<r<R, the force is zero as the mass of the hollow sphere is distributed on its surface. When the mass is positioned such that r≤R, the force will be,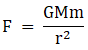
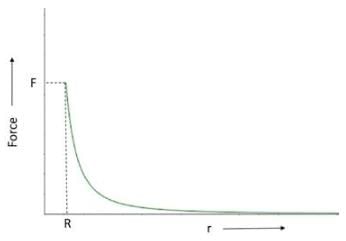 Therefore, the graph will be as follows
Therefore, the graph will be as follows
Q10: Out of aphelion and perihelion, where is the speed of the earth more and why ?
 View Answer
View Answer 
Ans: Aphelion is the location of earth from where it has the greatest distance from the sun and perihelion is the position from where it has the shortest distance. Now since the angular momentum of earth about the sun is conserved then we have:
mrap vap = mrpevpe
Where m is the mass of the earth, rap is the earth - sun distance at the aphelion and rpe is the earth - sun distance at the perihelion.
∴ rapvap = rpevpe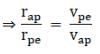
Since rap > rpe, vpe > vap, therefore the velocity at the perihelion is greater than the velocity at the aphelion.
Q11: What is the angle between the equatorial plane and the orbital plane of
(a) Polar satellite?
(b) Geostationary satellite?
 View Answer
View Answer 
Ans: The orbital plane of a satellite is the plane in which it revolves around the earth. The equatorial plane of earth is the plane which contains the equator.
(a) For a polar satellite, the satellite revolves from north to south and therefore its orbital plane is at 90° to the equatorial plane
(b) For a geostationary satellite whose position with respect to a place on earth is constant i.e. it revolves in the direction of the rotation of earth, the orbital plane is at 0° to the equatorial plane.
Part- 2
SHORT ANSWER TYPE QUESTIONS
Q1: Mean solar day is the time interval between two successive noon when sun passes through zenith point (meridian).
Sidereal day is the time interval between two successive transit of a distant star through the zenith point (meridian).
By drawing appropriate diagram showing earth’s spin and orbital motion, show that mean solar day is four minutes longer than the sidereal day. In other words, distant stars would rise 4 minutes early every successive day.
(Hint: you may assume circular orbit for the earth).
 View Answer
View Answer 
Ans: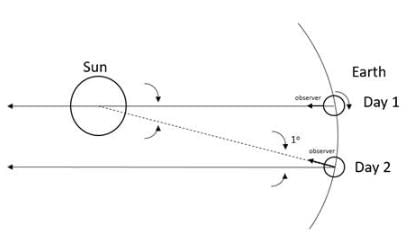
A day on earth is measured in terms of rotation of earth on its axis with respect to the sun called the mean solar day. When the day is measured with respect to a distant sun, it is called a sidereal day.
Let us look at the given figure, let the sun and distant star’s location be pointed by the long arrow at day 1, where they are directly in line with zenith of the observer on earth. When the earth rotates by 360° the arrow of the distant star points in the same direction along the zenith. However, the sun’s arrow is at an angle from the zenith. Thus, for the sun to be at the zenith in line with the observer, the earth needs to rotate an additional angle. Since the earth moves by 1° around the sun in a day, this additional angle is 1°. Now 360° is equal to 24 hours on earth or 1440 minutes, therefore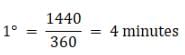
Therefore, the distant star will always rise 4 minutes earlier than the sun.
Q2: Two identical heavy spheres are separated by a distance 10 times their radius. Will an object placed at the mid point of the line joining their centres be in stable equilibrium or unstable equilibrium? Give reason for your answer.
 View Answer
View Answer 
Ans:
Given:
Distance between centres of spheres = 10 x radius
Let the mass of the two spheres be M and their radii be R. Then, the distance between the two will be 10R. let an object of mass m be placed at the midpoint of the line joining the centres of the spheres. Then the force acting on the object due to the two spheres F1 and F2 will be,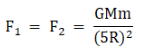
Therefore, the forces are equal and in opposite directions and therefore the mass is in stable equilibrium.
However, if the mass were to be displaced by say a distance x from the midpoint towards the sphere 2, the forces acting on the object would be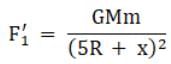
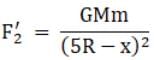
Therefore, F2’ > F1’ and therefore the net force acting on the mass will not be zero and equal to (F2’ - F1’) towards the sphere 2 and the object would be in unstable equilibrium.
Q3: Show the nature of the following graph for a satellite orbiting the earth.
(a) KE vs orbital radius R
(b) PE vs orbital radius R
(c) TE vs orbital radius R
 View Answer
View Answer 
Ans:
Given
Radius of satellite’s orbit = R
(a) Let the mass of earth be M and the mass of the satellite be m. Then the orbital velocity of the satellite will be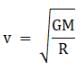
then, the kinetic energy of the satellite will be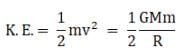
(b) the potential energy of the satellite is given by 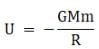
(c) the total energy of the satellite is given by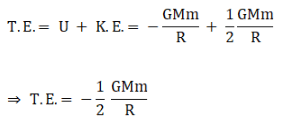
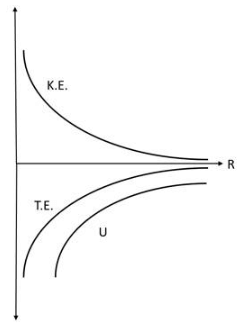
Therefore, the curves are as follows
Q4: Shown are several curves (Figure). Explain with reason, which ones amongst them can be possible trajectories traced by a projectile (neglect air friction).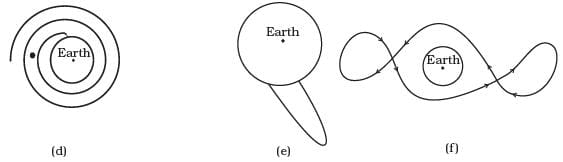
 View Answer
View Answer 
Ans: The trajectory or the path followed by a projectile under gravitational force of the earth instead of parabolic will be a conic section (for motion outside the earth) with the centre of the earth as a focus. Only the diagram in option (c) will fulfill the requirements.
Important point: In projectile we have taken the value of gravitational acceleration ‘g’ as a constant because up to some distance its variation will be neglected. The trajectory of the particle depends upon the velocity of projection. Depending upon the magnitude and direction of velocity it may be parabolic or elliptical.
Q5: An object of mass m is raised from the surface of the earth to a height equal to the radius of the earth, that is, taken from a distance R to 2R from the centre of the earth. What is the gain in its potential energy?
 View Answer
View Answer 
Ans:
Given:
Mass of the object = m
Radius of earth = R
Initial height of the object from earth’s centre = R
Final height of the object from earth’s centre = 2R
Let the mass of earth be M. We know that the gravitational potential energy of an object is given by,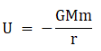
Where r is the distance between the object and centre of earth. When the object is at its initial position it is at a distance of R from the centre of the earth. Then its potential energy,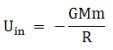
When the object is raised to a height 2R, then the potential energy is given by,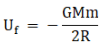
Now the gain in gravitational potential energy is given by
Q6: A mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r (Figure).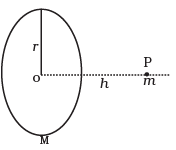
If the mass is removed further away such that OP becomes 2h, by what factor the force of gravitation will decrease, if h = r?
 View Answer
View Answer 
Ans:
Given:
Mass of the ring = M
Layout of the ring = r
Mass of the object = m
Initial distance of the object h = r
Final distance of the object 2h = 2r
To find the gravitational force on the object of mass m due to the ring let us consider an elemental mass on the ring of mass dM. The force due to this elemental mass is then,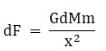
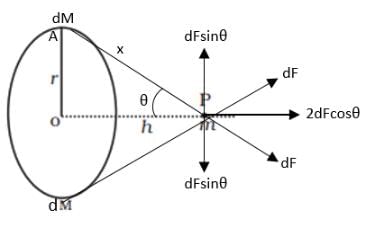
where x is the distance of the object from the elemental mass m and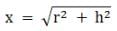
Now at the point P the force dF can be resolved into a vertical component and a horizontal component. If we consider two elemental masses diametrically opposite to each other, then the vertical component due to the two forces cancel each other as they are equal and opposite and the horizontal forces add up. Therefore, we only need to consider the horizontal component of the forces, therefore the net force on the object,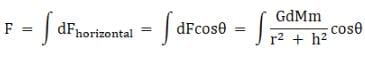
Now from the triangle OPA in the figure we have, 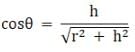
therefore, 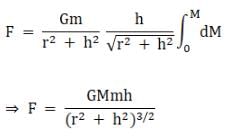
When h = r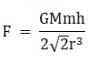
When h = 2h = 2r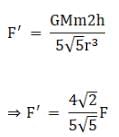
Therefore, the force decreases by a factor of 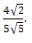
LONG ANSWER TYPE QUESTIONS
Q.1. A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum l. As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease.
 View Answer
View Answer 
Ans:
Given:
Radius of the orbit of planets = r
Let the mass of the sun be M and the planet be m.
(a) The force on an object revolving around the star is given by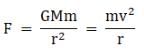
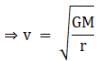
Therefore, linear velocity v is inversely proportional to square root of r and hence when r increases, v decreases.
(b) The angular velocity ω is given by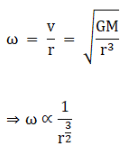
Therefore, when r increases, ω decreases.
(c) The kinetic energy K is given by,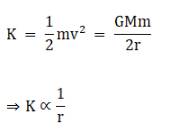
Therefore, as r increases, K decreases.
(d) The potential energy U is given by,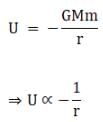
Therefore, as r increases U becomes less negative or increases.
(e) The total energy E is given by,
Therefore, as r increases E becomes less negative or increases.
(f) The angular momentum L is given by,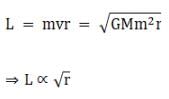
Therefore, as r increases, L increases.
Q2: Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
 View Answer
View Answer 
Ans:
Given
Side of hexagon = l
The force on the masses will be the resultant of the forces of all the other masses. Let the masses be m each. Now the distance AC is given by the parallelogram law i.e.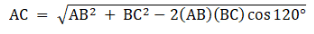

Due to symmetry we have AC = AE = 1√3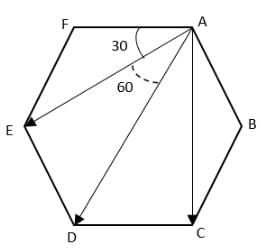
Now, for AD we have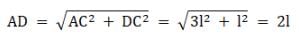
Now the force on mass at A due to b is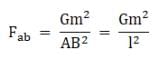
Also
Fab = Fat
The force on mass A due to C is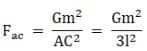
Also due to symmetry, we have
Fac = Fae
The force on mass at A due to mass at D is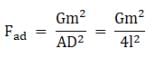
Now, the forces Fae and Fac make equal angles with the direction AD viz. 30°, and therefore by parallelogram law of vector addition their resultant is along AD and therefore the magnitude of the resultant,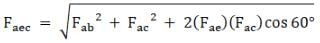
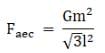
Similarly, Fab and Faf also make equal angles with AD viz. 60° and therefore they are also along AD and
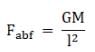
Therefore, the net force on mass at A will be
F = Faec + Fabf + Fad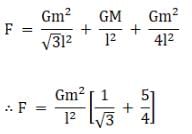
Q3: A satellite is to be placed in equatorial geostationary orbit around earth for communication.
(a) Calculate height of such a satellite.
(b) Find out the minimum number of satellites that are needed to cover entire earth so that at least one satellites is visible from any point on the equator.
[M = 6 × 1024 kg, R = 6400 km, T = 24h, G = 6.67 × 10–11 SI units]
 View Answer
View Answer 
Ans:
(a) For a geostationary satellite, the centripetal force must equal the gravitational force. Let the mass of earth be M and the satellite be m, then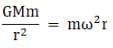
Where r is the radius of the orbit of the satellite and ω is its angular velocity
ω = 2π/T
where T is the time period of revolution, then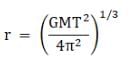
Now the height h of the satellite from the surface of the earth,
h = r - R
where R is the radius of earth.
For a geostationary satellite, the time period is 24 hours or 86400 seconds,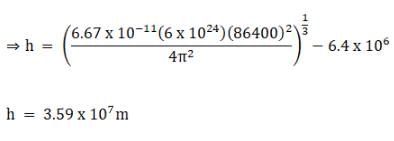
(b) A geostationary satellite is visible form the equator in the region shown in the figure having an angle 2θ,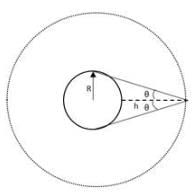
Now from the figure we have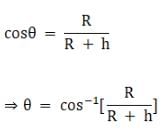
θ = cos-1[0.152] = 81.290
Now 2θ = 162.58, therefore to cover the earth with such satellites so that from any point on the equator a satellite can be seen,
360/162.58 = 2.21 ≈ 3
Q4: Earth’s orbit is an ellipse with eccentricity 0.0167. Thus, earth’s distance from the sun and speed as it moves around the sun varies from day to day. This means that the length of the solar day is not constant through the year. Assume that earth’s spin axis is normal to its orbital plane and find out the length of the shortest and the longest day. A day should be taken from noon to noon. Does this explain variation of length of the day during the year?
 View Answer
View Answer 
Ans:
Given
The eccentricity of earth’s orbit e = 0.0167
Let the earth - sun distance at the aphelion and perihelion be ra and rp respectively, and the angular velocity at those points be ωa and ωp. Now since the angular momentum of the earth is conserved we have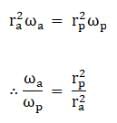
Now, from the ellipse we have
rp = a(1-e) and ra = a(a+e)
Where a is the semi - major axis of the ellipse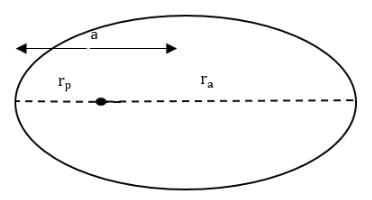
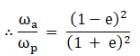
Since e = 0.0167
⇒ ωa/ωp = 1.069
And since the mean angular velocity is the geometric mean of the two, we have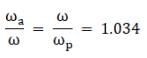
Now we know that the mean solar day corresponds to 1° on the orbit of earth. A mean solar day has 24 h for which the earth rotates 361°. Thus for aphelion the earth rotates 361.034° and hence the time for the day is 24 hours and 8.1 seconds, and the for the perihelion the earth rotates 359.96° and the time is 23 hours and 52 seconds. Thus the longest day is 8.1 seconds long and the shortest day is 8 seconds shorter. However, the variation of length of day in the year is not explained by this phenomenon as the total time of the day still remains around 24 hours, while the amount of time the sun is visible changes.
Q5: A satellite is in an elliptic orbit around the earth with aphelion of 6R and perihelion of 2 R where R= 6400 km is the radius of the earth. Find eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius 6R ?
[G = 6.67 × 10–11 SI units and M = 6 × 1024 kg]
 View Answer
View Answer 
Ans:
Given
Radius of earth = R = 6400 km
Aphelion earth - satellite distance ra = 6R
Perihelion earth - satellite distance rp = 2R
We know for an ellipse
rp = a(1-e) and ra = a(1+e)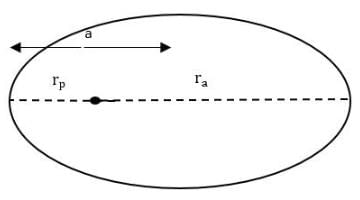
Where e is the eccentricity of the ellipse, and the semi major axis.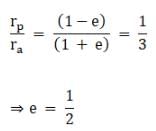
Now, the angular momentum of the satellite is conserved we then, we have
mrpvp=mrava
Where m is the mass of satellite and vp and va are the velocities at the perigee and apogee respectively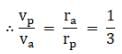
Now from conservation of energy at the apogee and perigee
KP + UP = Ka + Ua
Where K and U are the kinetic and gravitational potential energy of the satellite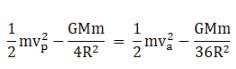
Where M is the mass of earth. Using the relation between vp and va above we have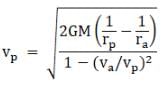
Putting the values of rp and ra we have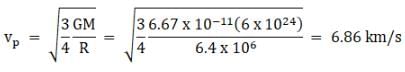
∴ va = vP/3 = 2.29 km/s
To transfer the satellite to a circular orbit of radius 6R the satellite’s velocity has to be maintained at a value of
|
95 videos|367 docs|98 tests
|
FAQs on NCERT Exemplar: Gravitation - Physics Class 11 - NEET
| 1. What is Newton's law of universal gravitation ? |  |
| 2. What is the significance of the gravitational constant (G) ? |  |
| 3. How does gravity affect the motion of planets and satellites ? |  |
| 4. What is the difference between weight and mass in the context of gravitation ? |  |
| 5. Why do astronauts feel weightless in space ? |  |

















