NCERT Exemplar: Kinetic Theory | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Multiple Choice Questions - II (More than one correct) |

|
| Very Short Answer Type Questions |

|
| Short Answer Questions |

|
| Long Answer Type Questions |

|
Multiple Choice Questions - I
Q1. A cubic vessel (with faces horizontal + vertical) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of 500m s–1 in the vertical direction. The pressure of the gas inside the vessel is observed by us on the ground.
(a) Remains the same because 500m s-1 is very much smaller than vrms of the gas.
(b) Remains the same because the motion of the vessel as a whole does not affect the relative motion of the gas molecules and the walls.
(c) Will increase by a factor equal to (v2rms + (500)2)/ v2rms where vrms was the original mean square velocity of the gas.
(d) Will be different on the top wall and bottom wall of the vessel.
Q. Choose the correct option.
Ans. (b)
Solution:
- According to the ideal gas law, P=nRT/V, here temperature of the vessel remains unchanged hence, the pressure remains the same from that point of view.
- Now, let us discuss the phenomenon inside the vessel. The gas molecules keep on colliding among themselves as well as with the walls of the containing vessel. These collisions are perfectly elastic.
- The number of collisions per unit volume in a gas remains constant. So, the pressure of the gas inside the vessel remains the same because the motion of the vessel as a whole does not affect the relative motion of the gas molecules with respect to the walls.
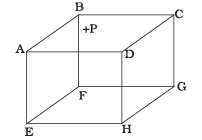
Q2. 1 mole of an ideal gas is contained in a cubical volume V, ABCDEFGH at 300 K (Figure). One face of the cube (EFGH) is made up of a material that absorbs any gas molecule incident on it. At any given time,
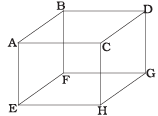
(a) The pressure on EFGH would be zero.
(b) The pressure on all the faces will be equal.
(c) The pressure of EFGH would be double the pressure on ABCD.
(d) The pressure on EFGH would be half that on ABCD.
Ans. (d)
Solution: In an ideal gas, the gas molecules keep on colliding among themselves as well as with the walls of containing vessel. These collisions are perfectly elastic. So, their kinetic energy and momentum remains conserved.
So, the momentum transferred to the face ABCD = 2mv And the gas molecule is absorbed by the face EFGH. Hence it does not rebound. So, momentum transferred to the face EFGH = mv.
And the pressure on the faces is due to the total momentum to the faces. So, pressure on EFGH would be half that on ABCD.
Q3. Boyle’s law is applicable for an
(a) Adiabatic process
(b) Isothermal process
(c) Isobaric process
(d) Isochoric process
Ans. (b)
Solution: Boyle’s law: For a given mass of an ideal gas at constant temperature, the volume of a gas is inversely proportional to its pressure.
So we can say that when temperature is constant, Boyle’s law is applicable.
i.e., PV= nRT= constant
⇒ PV = constant (at constant temperature)
i.e. p ∝ 1/V - [where, P = pressure. V= volume]
So, this law is applicable to an isothermal process, in which temperature remains constant.
Q4. A cylinder containing an ideal gas is in the vertical position and has a piston of mass M that is able to move up or down without friction in Figure. If the temperature is increased:

(a) Both p and V of the gas will change.
(b) Only p will increase according to Charle’s law.
(c) V will change but not p.
(d) p will change but not V.
Ans. (c)
Solution: The situation is shown in the diagram where an ideal gas is contained in a cylinder, having a piston of mass M.
According to the problem, the piston can move up and down without friction. So, the only force present is the weight of the piston.
The pressure inside the gas will be:
P = P0 + Mg/A = constant
where P0 = Atmospheric pressure
A = Area of cross-section of the piston
Mg = Weight of piston
The weight of the piston and atmospheric pressure are constant, hence pressure remains constant.
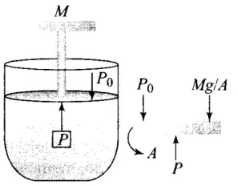
According to the ideal gas law:
PV = nRT
As the pressure remains constant, so if the temperature is increased, only the volume increases as the piston moves up without friction.
Q5. Volume versus temperature graphs for a given mass of an ideal gas are shown in Figure, at two different values of constant pressure. What can be inferred about the relation between P1 & P2?
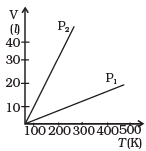
(a) P1 > P2
(b) P1 = P2
(c) P1 < P2
(d) Data is insufficient
Ans. (a)
Solution: We have to consider the slope of the V-T graph. From the ideal equation, the slope of the V-T curve is V/T = (nR/P).
So, if the slope is greater, pressure will be smaller and vice-versa.
We know for an ideal gas:
PV = nRT ⇒ V = (nR/P)T
Slope of the V-T graph, m = dV/dT = nR/P
⇒ m∝1/P [∴ nR = constant]
⇒ p ∝ 1/m
Hence, P1/P2 = m2/m1 < 1
So, P1 > P2.
where m1 is the slope of the graph corresponding to P1 and similarly m2 is the slope corresponding to P2.
Hence the correct option is (a), i.e. P1 > P2
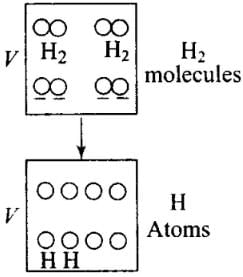
Q6. 1 mole of H2 gas is contained in a box of volume V = 1.00 m3 at T = 300K. The gas is heated to a temperature of T = 3000K and the gas gets converted to a gas of hydrogen atoms. The final pressure would be (considering all gases to be ideal)
(a) Same as the pressure initially
(b) 2 times the pressure initially
(c) 10 times the pressure initially
(d) 20 times the pressure initially
Ans. (d)
Solution: The situation is shown in the diagram, H2 gas is contained in a box is heated and gets converted to a gas of hydrogen atoms. Then the number of moles would become twice.
According to the gas equation:
PV= nRT
P = Pressure of gas, n = Number of moles
R = Gas constant, T = Temperature PV = nRT
As the volume (V) of the container is constant. Hence, when temperature (T) becomes 10 times, (from 300 K to 3000 K) pressure (P) also becomes 10 times, as P∝ T.
Pressure is due to the bombardment of particles and as gases break, the number of moles becomes twice of the initial, so n2 = 2n1
So P ∝ nT
⇒ 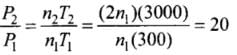
⇒ P2 = 20P1
Hence, the final pressure of the gas would be 20 times the pressure initially.
Q7. A vessel of volume V contains a mixture of 1 mole of Hydrogen and 1 mole of Oxygen (both considered ideal). Let f1 (v)dv, denote the fraction of molecules with speed between v and (v + dv) with f2 (v)dv, similarly for oxygen. Then
(a) f1(v) + f2 (v)= f (v) obeys the Maxwell’s distribution law.
(b) f1( v), f2 (v) will obey Maxwell’s distribution law separately.
(c) Neither f1 (v) nor f2 (v) will obey Maxwell’s distribution law.
(d) f2 (v) and f1 (v) will be the same.
Ans. (c)
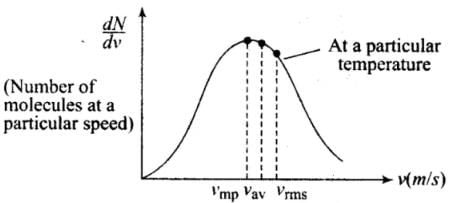
Solution: Maxwell’s Law (or the Distribution of Molecular Speeds:
(1) The vrms gives us a general idea of molecular speeds in a gas at a given temperature. This doesn’t mean that the speed of each molecule is vrms. Many of the molecules have speeds less than vrms and many have speeds greater than vrms.
(2) Maxwell-derived equation gives the distribution of molecules at different speeds as follows: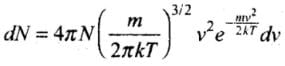
where dN = Number of molecules with speeds between v and v + dv
The masses of hydrogen and oxygen molecules are different.
For a function f(v), the number of molecules dn = f[v), which have speeds between v and v + dv.
The Maxwell-Boltzmann speed distribution function ( Nv = dn/dv depends on the mass of the gas molecules.
For each function f1(v) and f2(v), n will be different, hence each function f1(v) and f2(v) will obey Maxwell’s distribution law separately.
Q8. An inflated rubber balloon contains one mole of an ideal gas, and has a pressure p, volume V, and temperature T. If the temperature rises to 1.1 T, and the volume is increased to 1.05 V, the final pressure will be
(a) 1.1 P
(b) P
(c) Less than P
(d) Between P and 1.1
Ans. (d)
Solution: According to the equation of ideal gas, PV= nRT
P = pressure
V = volume
n = number of moles of gases
R = gas constant
T = temperature
Thus we have to rewrite this equation in such a way that no. of moles is given by,
n = PV/RT
As number of moles of the gas remains fixed, hence, we can write: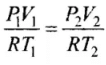
⇒ 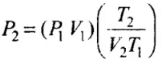
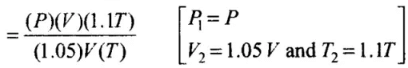

Hence, final pressure P2 lies between P and 1.1 P.
Multiple Choice Questions - II (More than one correct)
Q.9. ABCDEFGH is a hollow cube made of an insulator (Fig.). Face ABCD has a positive charge on it. Inside the cube, we have ionized hydrogen.
The usual kinetic theory expression for pressure:
(a) Will be valid.
(b) Will not be valid since the ions would experience forces other than due to collisions with the walls.
(c) Will not be valid since collisions with walls would not be elastic.
(d) Will not be valid because isotropy is lost.
Ans. (b, d)
Solution: According to the problem, ionized hydrogen is present inside the cube, they have a charge. Now, due to the presence of a positive charge on the surface, ABCD hydrogen ions would experience forces other than the forces due to collision with the walls of the container. So, these forces must be of electrostatic nature. Hence, the Isotropy of the system is lost at only one face ABCD because of the presence of an external positive charge. The usual expression for pressure on the basis of kinetic theory will be valid.
Q10. Diatomic molecules like hydrogen have energies due to both translational as well as rotational motion. From the equation in kinetic theory pV = 2/3 E, E is
(a) The total energy per unit volume.
(b) Only the translational part of energy because rotational energy is very small compared to the translational energy.
(c) Only the translational part of the energy because during collisions with the wall pressure relates to the change in linear momentum.
(d) The translational part of the energy because rotational energies of molecules can be of either sign and its average over all the molecules is zero.
Ans. (c)
Solution: According to kinetic theory equation, PV = 2/3 E [where P= Pressure V = volume]
E represents only the translational part of energy. Internal energy contains all types of energy like translational, rotational, vibrational etc. However the molecules of an ideal gas is treated as point masses in kinetic theory, so its kinetic energy is only due to translational motion.
Point mass does not have rotational or vibrational motion. Here, we assumed that the walls only exert perpendicular forces on molecules. They do not exert any parallel force, hence there will not be any type of rotation present. The wall produces only change in translational motion.
Q11. In a diatomic molecule, the rotational energy at a given temperature
(a) Obeys Maxwell’s distribution.
(b) Have the same value for all molecules.
(c) Equals the translational kinetic energy for each molecule.
(d) Is (2/3)rd the translational kinetic energy for each molecule.
Ans. (a, d)
Solution: Consider a diatomic molecule along the z-axis so its rotational energy about the z-axis is zero. So the energy of diatomic molecule.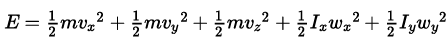 (as the moment of inertia along the axis is zero)
(as the moment of inertia along the axis is zero)
The independent term in the above expression is 5. We can predict the velocities of molecules by Maxwell’s distribution. Hence the above expression also obeys Maxwell’s distribution. As 2 rotational and 3 translational energies are associated with each molecule. So the rotational energy at a given temperature is 2/3 of the translational Kinetic energy of each molecule.
Q12. Which of the following diagrams (Figure) depicts ideal gas behavior?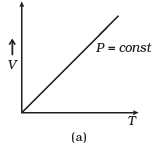
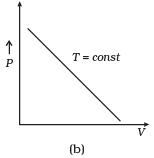
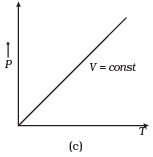
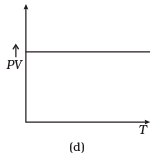
Ans. (a, c)
Solution: For ideal gas behavior,
PV = nRT ...(i)
(a) When pressure, P = constant
From (i) Volume (V) ∝ Temperature (T)
The graph of V versus T will be a straight line.
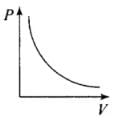
(b) When T = constant
From (i) PV = constant
So, the graph of P versus V will be a rectangular hyperbola. Hence this graph is wrong.
The correct graph is shown below:
(c) When V = constant.
From (i) P ∝ T
So, the graph is a straight line passing through the origin.
(d) From (i) PV ∝ T
⇒ PV/T = constant
So, the graph of PV versus T will be a straight line parallel to the temperature axis(x-axis).
i.e., the slope of this graph will be zero.
So, (d) is not correct.
Q13. When an ideal gas is compressed adiabatically, its temperature rises: the molecules on the average have more kinetic energy than before. The kinetic energy increases:
(a) Because of collisions with moving parts of the wall only.
(b) Because of collisions with the entire wall.
(c) Because the molecules get accelerated in their motion inside the volume.
(d) Because of redistribution of energy amongst the molecules.
Ans. (a)
Solution: Since the gas is ideal and the collisions of the molecules are elastic. When the molecules collide with the moving parts of the wall, their kinetic energy increases. However, the total kinetic energy of the system will remain conserved. When the gas is compressed adiabatically, the total work done on the gas increases, its internal energy which in turn increases the KE of gas molecules, and hence, the collisions between molecules also increase.
Very Short Answer Type Questions
Q1. Calculate the number of atoms in 39.4 g gold. The molar mass of gold is 197 g mole-1.
Ans. Here, we know that,
Molar mass = Mass of Avogadro's number of atoms (Molecules)
= 6.023 x 1023 atoms.
According to the problem:
Mass of the gold, m = 39.4 g
The molar mass of the gold, M = 197 g mol-1
Now, 197 g of gold contains 6.023 x 1023 atoms
So, 1 g of gold contains 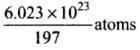
∴ 39.4 g of gold contains (6.023 x 1023 x 39.4)/ 197 atoms = 1.20 x 1023 atoms
Q2. The volume of a given mass of a gas at 27°C, 1 atm is 100 cc. What will be its volume at 327°C?
Ans. By gas equation of ideal gas:
P1 = 1atm, P2 = 1 atm, V1 = 100 cc, V2 = ?
T1 = 273 + 27 = 300 K
T2 = 327 + 273 = 600K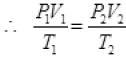
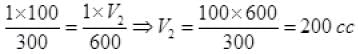
Units of (P1, P2) and (V1, V2) must be the same separately but a unit of T must be in only on the Kelvin scale.
Q3. The molecules of a given mass of gas have root mean square speeds of 100 m s-1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
Ans. vrms = 100 m/s
T1 = 27 + 273 = 300K
v2rms = ?
T2 = 127 + 273 = 400K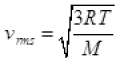
M = Molar mass of gas for a gas M is constant
∴ vrms ∝ √T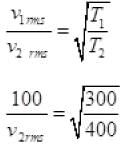
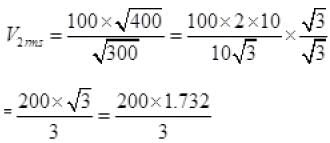
v2rms =115.4 ms-1.
Q4. Two molecules of a gas have speeds of 9 × 106 ms-1 and 1 ×106 ms-1, respectively. What is the root mean square speed of these molecules?
Ans. RMS speed for w-molecules is defined as: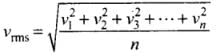 [vrms = root mean square velocity]
[vrms = root mean square velocity]
where v1, v2, v1, ...vn are individual velocities of n - molecules of the gas.
For two molecules,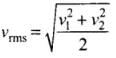
According to the problem, v1 = 9 x 106 m/s and v2 = 1 x 106 m/s
∴ 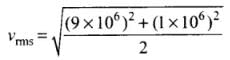
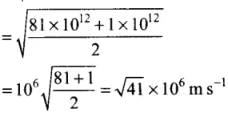
Q5. A gas mixture consists of 2.0 moles of oxygen and 4.0 moles of neon at temperature T. Neglecting all vibrational modes, calculate the total internal energy of the system. (Oxygen has two rotational modes.)
Ans. According to the problem:
n0 = 2 moles, nn = 4 moles
Temperature of the gas = T
Since oxygen is a diatomic gas. So, the degree of freedom associated with the molecules of oxygen is 5.
Energy (total internal) per mole of the gas = 5/2 RT
[R = universal gas constant
T = temperature]
For 2 moles of the gas total internal energy = 2 x 5/2 RT = 5RT ...(i)
Neon (Ne) is a monoatomic gas having 3 degrees of freedom.
Energy per mole = 3/2RT
Hence, Energy = 4 x 3/2 RT = 6RT ….(ii)
[Using Eqs. (i) and (ii)]
Total energy = 5RT = 6RT= 11RT
Q6. Calculate the ratio of the mean free paths of the molecules of two gases having molecular diameters 1A and 2A. The gases may be considered under identical conditions of temperature, pressure, and volume.
Ans. Mean Free Path:
The distance traveled by a gas molecule between two successive collisions is known as the free path.
λ = Total distance travelled by a gas molecule between successive collisions / Total number of collisions during two successive collisions
A molecule of a gas moves in a straight line with constant velocity. Let λ1, λ2 , λ3 be the distance traveled by a gas molecule during n collisions respectively, then the mean free path of a gas molecule is given by:
λ = 
where d = Diameter of the molecule,
n = Number of molecules per unit volume
According to the problem:
d1 = 1 Å: d2 = 2Å
Since mean free path,
λ ∝ 1/d2
⇒So, 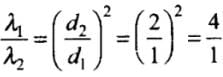
Hence, λ1 : λ2 = 4 : 1
Short Answer Questions
Q1.The container shown in Figure has two chambers, separated by a partition, of volumes V1 = 2.0 liter and V2= 3.0 liter. The chambers contain µ1 = 4.0 and µ2 = 5.0 moles of a gas at pressures p1 = 1.00 atm and p2 = 2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium. Ans. V1 = 2.0 litre V2 = 3.0 litre
Ans. V1 = 2.0 litre V2 = 3.0 litre
µ1 = 4.0 moles µ2 = 5.0 moles
P1 = 1.00 atm P2 = 2.00 atm
P1V1 = µ1RT1
P2V2 = µ2 RT2
µ = µ1 + µ2
V = V1 V2
For 1 mole PV = 2/3 E
For µ1 moles 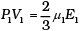
For µ2 moles 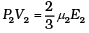
Total energy is 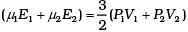
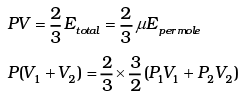
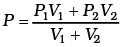
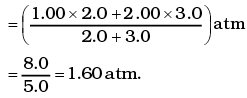
This form of ideal gas law represented by Equation marked becomes very useful for adiabatic changes.
Q2. A gas mixture consists of molecules of types A, B, and C with masses mA > mB > mC. Rank the three types of molecules in decreasing order of (a) average K.E., (b) rms speeds.
Ans. The average K.E will be the same as conditions of temperature and pressure are the same
vrms α 1/√m
∵ mA > mB > mC
vC > vB > vA
Q3. We have 0.5 g of hydrogen gas in a cubic chamber of size 3 cm kept at NTP. The gas in the chamber is compressed keeping the temperature constant till a final pressure of 100 atm. Is one justified in assuming the ideal gas law, in the final state?
(Hydrogen molecules can be considered as spheres of radius 1 Å).
Ans. We have 0.25 × 6 × 1023 molecules, each of volume 10-30m3.
Molecular volume = 2.5 × 10-7m3
Supposing Ideal gas law is valid.
Final volume 
which is about the molecular volume. Hence, intermolecular forces cannot be neglected. Therefore the ideal gas situation does not hold.
Q4. When air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Boyle’s law in this case?
Ans. According to Boyle’s law; at a constant temperature the volume of gas is inversely proportional to pressure i.e. It is valid only for a constant mass of gas. But in this case when air is pumped continuously into the tyre, so number of moles of air increases. So Boyle’s or gas laws are not valid in this case.
Q5. A balloon has 5.0 g mole of helium at 7°C. Calculate
(a) the number of atoms of helium in the balloon,
(b) the total internal energy of the system.
Ans. For gas helium n = 5 mole
T = 7 + 273 = 280 K
(a) The number of atoms of he is 5 mole = 5 x 6.023 x 1023 atoms
= 30.115 x 1023 atoms
= 3.0115 x 1024 He atoms.
(b) The atom is monoatomic so the degree of freedom is 3. So the average kinetic energy
= 3/2 KBT Per molecule
= 3/2 KBT x Number of He Atom
= 3/2 x 1.38 x 10-23 x 280 x 3.0115 x 1024
Total E of 15 mole of He = 1.74 x 104 J
Q6. Calculate the number of degrees of freedom of molecules of hydrogen in 1 cc of hydrogen gas at NTP.
Ans. The volume occupied by 1 gram mole of gas at NTP = 22400cc
∴ Number of molecules in 1 cc of hydrogen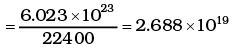
As each diatomic molecule has 5 degrees of freedom, hydrogen being diatomic also has 5 degrees of freedom
∴ Total no of degrees of freedom = 5 × 2.688 × 1019 = 1.344 x 1020
Q7. An insulated container containing monoatomic gas of molar mass m is moving with a velocity vo. If the container is suddenly stopped, find the temperature change.
Ans. Loss in K.E of the gas = ΔE = 1/2(mn)v02
where n = no: of moles.
If its temperature changes by ∆T, then
= n(3/2)RΔT
= 1/2mn v02.
∴ ΔT = 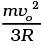
Long Answer Type Questions
Q1. Explain why
(a) there is no atmosphere on the moon.
(b) there is a fall in temperature with altitude.
Ans. The moon has a small gravitational force and hence the escape velocity is small. As the moon is in the proximity of the Earth as seen from the Sun, the moon has the same amount of heat per unit area as that of the Earth. The air molecules have a large range of speeds. Even though the rms speed of the air molecules is smaller than the escape velocity on the moon, a significant number of molecules have speed greater than escape velocity and they escape. Now rest of the molecules arrange the speed distribution for the equilibrium temperature. Again a significant number of molecules escape as their speeds exceed escape speed. Hence, over a long time, the moon has lost most of its atmosphere.
At 300 K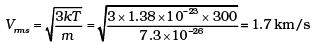
Vesc for moon = 4.6 km/s
(b) As the molecules move higher their potential energy increases and hence kinetic energy decreases and hence temperature reduces.
At greater height more volume is available and gas expands and hence some cooling takes place.
Q2. Consider an ideal gas with the following distribution of speeds.
| Speed (m/s) | % of molecules |
| 200 | 10 |
| 400 | 20 |
| 600 | 40 |
| 800 | 20 |
| 1000 | 10 |
(i) Calculate Vrms and hence T. (m = 3.0× 10−26 kg)
(ii) If all the molecules with a speed of 1000 m/s escape from the system, calculate new Vrms and hence T.
Ans. (This problem is designed to give an idea about cooling by evaporation)
(i) 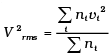
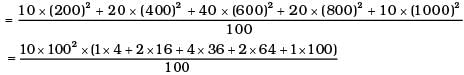
= 1000 × (4 + 32 + 144 +128 + 100) = 408 ×1000 m2/s2
∴ vrms = 639 m/s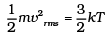
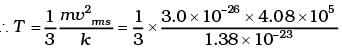
= 2.96 ×102K = 296K
(ii) 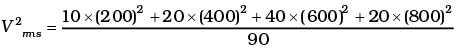
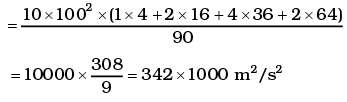
vrms = 584 m/s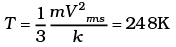
Q3. Ten small planes are flying at a speed of 150 km/h in total darkness in an air space that is 20 × 20 × 1.5 km3 in volume. You are in one of the planes, flying at random within this space with no way of knowing where the other planes are. On average about how long a time will elapse between near collision with your plane. Assume for this rough computation that a safety region around the plane can be approximated by a sphere of radius 10m.
Ans. Planes can be considered as the motion of molecules in confined space. Time of relaxation for mean free path λ is the distance between two planes traveled between the collision or just to avoid an accident.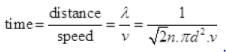
N = number of particles per unit volume V = N/Volume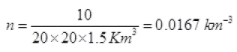
d = 2 x 10 m = 20 m = 20 x 10-3 km, v = 150 Km/hr
∴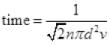

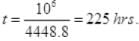
Q4. A box of 1.00m3 is filled with nitrogen at 1.50 atm at 300K. The box has a hole of an area of 0.010 mm2. How much time is required for the pressure to reduce by 0.10 atm, if the pressure outside is 1 atm.
Ans. Volume of box = 1m3 =V1
Initial pressure = 1.5 atm = P1
Final pressure = 1.5 – 0.1 = 1.4 atm =P’2
Air pressure outside box = P2 = 1 atm
Initial temperature T1 = 300K
Final temperature T2 = 300K
a = area of hole = 0.01 mm2 = 0.01 x 10-6 m2 = 10-8 m2
the initial pressure difference between tyre and atmosphere ΔP = (1.5 - 1)atm
mass of a N2 gas molecule = 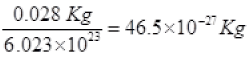
KB = 1.38 x 10-23
Let Pn1 be the initial number of N2 gas molecules per unit volume in time Δt Let vix be the speed of molecules along the axis
Number of molecules colliding in time Δt on a wall of cube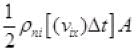
1/2 is multiplied as the other 1/2 molecule will strike to the opposite wall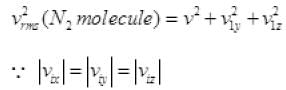
Then 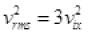
KE of gas molecule = 3/2 KBT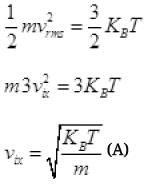
Number of N2 gas molecules striking a wall in Δt time Outward = 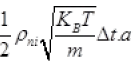 out
out
The temperature inside the box and the air is equal to T
The number of air molecules striking to hole in Δt
inward = 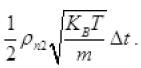
ρn2 = density of air molecule
The net number of molecules (going outward)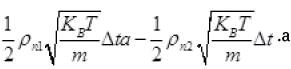
The net number of molecules going out from the hole in Δt time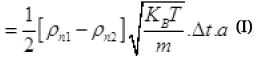
Gas equation 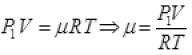
As for box  (μ = No. of moles of gas in box)
(μ = No. of moles of gas in box)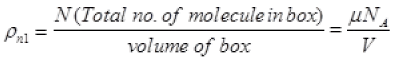
= P1NA/RT Per unit volume
Let after time T pressure reduced by 0.1 and becomes (1.5 - 1) = 1.4 atm P'2
The final new density of NA molecule ρ'n1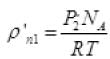 Per unit volume (III)
Per unit volume (III)
The net number of molecules going out from volume V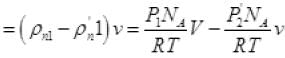
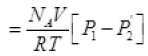 (iv) (from II, III)
(iv) (from II, III)
P2 = final pressure of box
From (I) the total number of molecules going out in time τ from the hole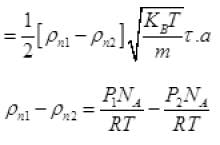
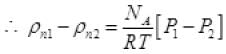 (P2 = Press of air out of the box)
(P2 = Press of air out of the box)
Net number of molecules going out in τ time from above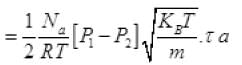
From (V) and IV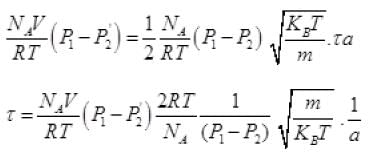
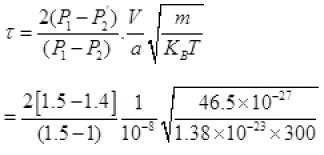
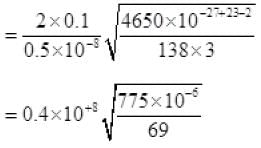
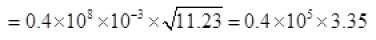
τ = 1.34 x 105 seconds
Q5. Consider a rectangular block of wood moving with a velocity v0 in gas at temperature T and mass density ρ. Assume the velocity is along the x-axis and the area of the cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is where m is the mass of the gas molecule.
Ans. n = no. of molecules per unit volume
vrms = rms speed of gas molecules
When the block is moving with speed vo, the relative speed of molecules w.r.t. front face = v + vo
Coming head-on, momentum transferred to block per collision
= 2m (v+vo), where m = mass of molecule.
No. of collision in time 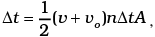 where A = area of cross-section of block and factor of 1/2 appears due to particles moving towards the block.
where A = area of cross-section of block and factor of 1/2 appears due to particles moving towards the block.
∴ Momentum transferred in time Δt = m(v + v0)2 nAΔt from front surface
Similarly momentum transferred in time Δt = m(v + v0)2 nAΔt from back surface
∴ Net force (drag force) = mnA[(v + v0) - (v - v0)2] from front
= mnA (4vvo) = (4mnAv)vo
= (4ρAv)vo
We also have 1/2 mv2 = 1/2kT (v - is the velocity along the x-axis)
Therefore, 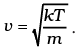
Thus drag 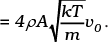
|
96 videos|367 docs|98 tests
|
FAQs on NCERT Exemplar: Kinetic Theory - Physics Class 11 - NEET
| 1. What is the kinetic theory of matter? |  |
| 2. What are the assumptions of the kinetic theory of matter? |  |
| 3. How does the kinetic theory explain the pressure exerted by gases? |  |
| 4. How does the kinetic theory explain the expansion of matter on heating? |  |
| 5. How does the kinetic theory explain the relationship between temperature and kinetic energy? |  |





















