NCERT Exemplar: Laws of Motion | Physics Class 11 - NEET PDF Download
MULTIPLE CHOICE QUESTIONS
Q.1. A ball is travelling with uniform translatory motion. This means that
(a) It is at rest.
(b) The path can be a straight line or circular and the ball travels with uniform speed.
(c) All parts of the ball have the same velocity (magnitude and direction) and the velocity is constant.
(d) The centre of the ball moves with constant velocity and the ball spins about its centre uniformly.
 View Answer
View Answer 
Ans. (c)
Solution.
When a body moves in such a way that the linear distance covered by each particle of the body is same during the motion, then the motion is said to be translatory or translation motion.
Translatory motion can be, again of two types viz., curvilinear (shown in fig. (a)) or rectilinear (shown in fig. (b)), accordingly as the paths of every constituent particles are similarly curved or straight line paths. Here it is important that the body does not change its orientation. Here we can also define it further in uniform and non-uniform translatory motion. Here figure
(b) is uniformly translatory motion.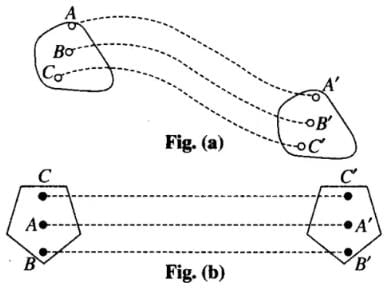
Q.2. A metre scale is moving with uniform velocity. This implies
(a) The force acting on the scale is zero, but a torque about the centre of mass can act on the scale.
(b) The force acting on the scale is zero and the torque acting about centre of mass of the scale is also zero.
(c) The total force acting on it need not be zero but the torque on it is zero.
(d) Neither the force nor the torque need to be zero.
 View Answer
View Answer 
Ans. (b)
Solution.
As the meter, the scale is moving with uniform velocity.
∴ No change in its velocity i.e., acceleration of it zero by Newton’s second law 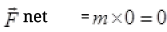
∴ Hence net or resultant force must act on body zero.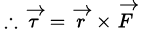
So torque must be zero.
Hence, for uniform motion force and torque, both must be zero.So, It verifies the option (b).
Q.3. A cricket ball of mass 150 g has an initial velocity 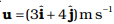 and a final velocity
and a final velocity 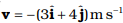 after being hit. The change in momentum (final momentum-initial momentum) is (in kg m s1)
after being hit. The change in momentum (final momentum-initial momentum) is (in kg m s1)
(a) zero
(b)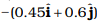
(c)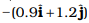
(d)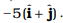
 View Answer
View Answer 
Ans. (c)
Solution.
m = 150g = 0.15kg
Change in momentum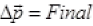 momentum-Initial momentum
momentum-Initial momentum 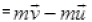
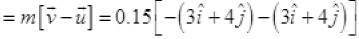
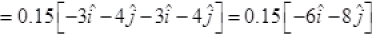
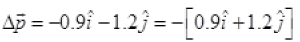
Hence, this verifies the option(c).
Q.4. In the previous problem (5.3), the magnitude of the momentum transferred during the hit is
(a) Zero
(b) 0.75 kg m s–1
(c) 1.5 kg m s–1
(d) 14 kg m s–1
 View Answer
View Answer 
Ans. (c)
Solution.
By previous solution,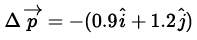
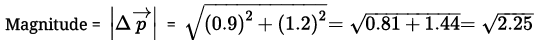
= 1.5 kg ms-1
So, this verifies the option (c).
Q.5. Conservation of momentum in a collision between particles can be understood from
(a) Conservation of energy.
(b) Newton’s first law only.
(c) Newton’s second law only.
(d) Both Newton’s second and third law.
 View Answer
View Answer 
Ans. (d)
Solution.
(i) By Newton’s second law 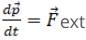
As 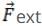 in law of conservation of momentum is zero.
in law of conservation of momentum is zero.
i.e., 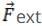 = 0
= 0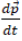 = 0
= 0
⇒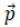
(ii) By Newton’s third law action force is equal to reaction force in magnitude but in opposite direction.
∴ 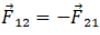 (
(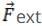 = 0)
= 0)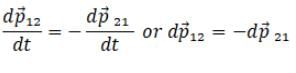
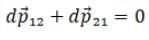
So proves the law of conservation of momentum and verifies the option (d).
Q.6. A hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponet. The force that acts on the player is.
(a) Frictional force along westward.
(b) Muscle force along southward.
(c) Frictional force along south-west.
(d) Muscle force along east-west.
 View Answer
View Answer 
Ans. (c)
Solution.
Step 1: Understand the Initial and Final Directions
The hockey player is initially moving northward. When he turns to move westward, he changes his direction but maintains the same speed.
Step 2: Analyze the Change in Momentum
Momentum is a vector quantity defined as the product of mass and velocity. The change in momentum occurs due to the change in direction.
- Initial momentum (P1) is directed north.
- Final momentum (P2) is directed west.
Step 3: Determine the Change in Momentum
The change in momentum (ΔP) can be calculated as:
ΔP = P2 − P1
This represents a vector subtraction where you find the resultant vector from the initial and final momentum vectors.
Step 4: Find the Direction of the Change in Momentum
To find the direction of ΔP, you can visualize the initial and final momentum vectors. The change in momentum vector will point from the initial direction (north) to the final direction (west).
This results in a vector that points diagonally between the north and west directions, which is southwest.
Step 5: Relate the Change in Momentum to Force
According to Newton's second law, the force acting on an object is equal to the rate of change of momentum. Thus, the direction of the force will be the same as the direction of the change in momentum.
Step 6: Identify the Type of Force
In this scenario, the force acting on the hockey player is primarily due to friction, which allows him to change direction while maintaining speed. The direction of this frictional force is southwest, as derived from the change in momentum.
Conclusion
The force that acts on the hockey player when he turns from north to west while maintaining the same speed is a frictional force directed southwest.
Q.7. A body of mass 2kg travels according to the law x(t) = pt + qt2 + rt3 where p = 3ms−1 , q = 4ms−2 = and r = 5ms−3.
The force acting on the body at t = 2 seconds is
(a) 136 N
(b) 134 N
(c) 158 N
(d) 68 N
 View Answer
View Answer 
Ans. (a)
Solution.
To find the force acting on the body at t = 2 s, we follow these steps:
Step 1: Equation for acceleration
The position of the body as a function of time is given by: x(t) =pt + qt2 + rt3
where p= 3m/s, q = 4m/s2, r =5m/s3.
Velocity is the first derivative of position:
v(t) = dx/dt =p + 2qt + 3rt2
Acceleration is the first derivative of velocity:
a(t) = dv/dt = 2q + 6rt
Step 2: Compute acceleration at t = 2 s
Substitute q = 4m/s2 and r = 5 m/s3 into a(t):
a(t) = 2q + 6rt
a(2) = 2(4) +6(5)(2) = 8 + 60 = 68m/s2
Step 3: Compute force
The force acting on the body is given by Newton's second law:
F = ma
Substitute m = 2 kg and a = 68 m/s2:
F = 2 x 68 = 136N
Q.8. A body with mass 5 kg is acted upon by a force 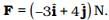 If its initial velocity at t = 0 is
If its initial velocity at t = 0 is 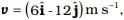 the time at which it will just have a velocity along the y-axis is
the time at which it will just have a velocity along the y-axis is
(a) Never
(b) 10 s
(c) 2 s
(d) 15 s
 View Answer
View Answer 
Ans. (b)
Solution.
To determine when the body will have a velocity only along the y-axis, we need to analyze the motion of the body under the given force.
Step 1: Force and acceleration
The force acting on the body is related to the acceleration by Newton's second law: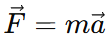 where m = 5kg.
where m = 5kg.
Let the components of the force be Fx and Fy, and the corresponding accelerations be ax = Fx/m and ay = Fy/m.
Step 2: Initial velocity
Let the initial velocity of the body be 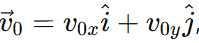 where
where 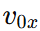 and
and 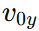 are the initial components along the x- and y-axes.
are the initial components along the x- and y-axes.
At time t, the velocity components are: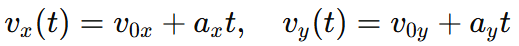
For the body to have a velocity only along the y-axis, the x-component of velocity must be zero: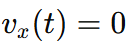
Step 3: Solve for t
From 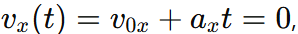 we get:
we get: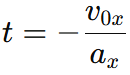
Step 4: Conditions for t
- If
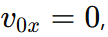 the body already has no x-component of velocity.
the body already has no x-component of velocity. - If
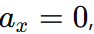 the x-component of velocity will never change.
the x-component of velocity will never change. - If
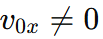 and
and  substitute the values of
substitute the values of 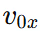 and ax to calculate t.
and ax to calculate t.
Q.9. A car of mass m starts from rest and acquires a velocity along east 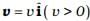 in two seconds. Assuming the car moves with uniform acceleration, the force exerted on the car is
in two seconds. Assuming the car moves with uniform acceleration, the force exerted on the car is
(a) mv/2 eastward and is exerted by the car engine.
(b) mv/2 eastward and is due to the friction on the tyres exerted by the road.
(c) more than mv/2 eastward exerted due to the engine and overcomes the friction of the road.
(d) mv/2 exerted by the engine.
 View Answer
View Answer 
Ans. (b)
Solution. Here, mass of car = m
As it starts from rest, u = 0 final velocity along east υ = υî , t = 2 sec
Fromυ = u + at
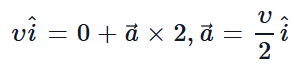 force of car is mv/2 east ward
force of car is mv/2 east ward
This is due to friction on the tyres exerted by the road.
Q.10. The motion of a particle of mass m is given by x = 0 for t < 0 s, x(t) = A sin4p t for 0 < t <(1/4) s (A > o), and x = 0 for t >(1/4) s. Which of the following statements is true?
(a) The force at t = (1/8) s on the particle is –16π2 A m.
(b) The particle is acted upon by on impulse of magnitude 4π2 A m at t = 0 s and t = (1/4) s.
(c) The particle is not acted upon by any force.
(d) The particle is not acted upon by a constant force.
(e) There is no impulse acting on the particle.
 View Answer
View Answer 
Ans. (a, b, d)
Solution.
We have given mass = m, x(t) = 0 for t < 0
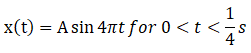
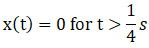
Now let’s look for time interval 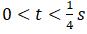
x(t) = A sin 4πt
Also we know,
1st derivative of x(t) w.r.t. time will give velocity
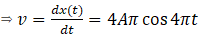
2nd derivative of x(t) w.r.t. time will give velocity
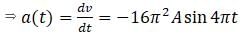
Then,

Here, this force is obviously time dependent so force is not constant hence option (d) is correct.
Now let’s look to option (a) i.e. At 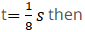
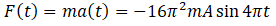
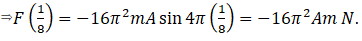
So from this we can say option (a) also correct.
Now for option (b) i.e. between t = 0 s and t = (1/4) s, as we know impulse is change in momentum or 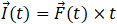 so at t = (1/4) s impulse will be
so at t = (1/4) s impulse will be
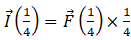 here we have to keep in mind that F(t) varies from t=0 to maximum 1/8 s, so F (1/4) will be replaced by F (1/8) also from above we have found
here we have to keep in mind that F(t) varies from t=0 to maximum 1/8 s, so F (1/4) will be replaced by F (1/8) also from above we have found
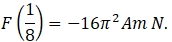
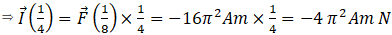
so option(b) is also correct.
Option (c) is absolutely wrong as we have above found that force is acting.
Option (e) is also wrong because we have already calculated the impulse.
Q.11. In Fig, the co-efficient of friction between the floor and the body B is 0.1. The co-efficient of friction between the bodies B and A is 0.2. A force F is applied as shown on B. The mass of A is m/2 and of B is m. Which of the following statements are true?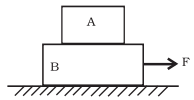 (a) The bodies will move together if F = 0.25 mg.
(a) The bodies will move together if F = 0.25 mg.
(b) The body A will slip with respect to B if F = 0.5 mg.
(c) The bodies will move together if F = 0.5 mg.
(d) The bodies will be at rest if F = 0.1 mg.
(e) The maximum value of F for which the two bodies will move together is 0.45 mg.
 View Answer
View Answer 
Ans. (a, b, d, e)
Solution.
We have given 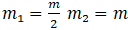 Let acceleration in body A and B is ‘a’.
Let acceleration in body A and B is ‘a’.
Body A will move along with body B by force F till the force of friction between surface of A and B is larger or equal to zero.
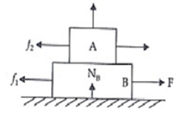 Now taking system A+B then acceleration will be
Now taking system A+B then acceleration will be
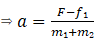
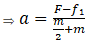
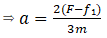
So force on A
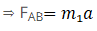

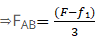
If FAB is equal or smaller than f2 then body A will move along with body B.
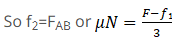
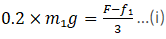
N = Reaction force by B on A
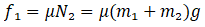
[N2 = Normal reaction on B along with A by surface]
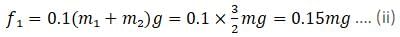
From (i)
 so adding this with equation (ii) we can say F = 0.45mg ...(iii)
so adding this with equation (ii) we can say F = 0.45mg ...(iii)
F = 0.45mg Newton is the maximum force on B. so that A and B can move together. So option (e) is correct.
Both bodies can move together if F is less than or equal to 0.45mg Newton.
So options (a) and (b) are also correct and rejects the option (c) as 0.5mg>0.45mg.
For option (d): Minimum force which can move A and B together
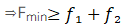
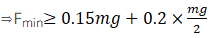
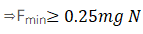
Given force in option (d) 0.1mg Newton <0.25mg Newton. So body A and B will not move i.e.
Bodies A and B will remain in rest hence option (d) is also correct.
Q.12. Mass m1 moves on a slope making an angle θ with the horizontal and is attached to mass m2 by a string passing over a frictionless pulley as shown in Fig. The co-efficient of friction between m1 and the sloping surface is µ.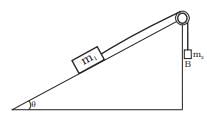 (a) If m2 > m1 sin θ, the body will move up the plane.
(a) If m2 > m1 sin θ, the body will move up the plane.
(b) If m2 > m1 > + (sinθ + µ cos θ), the body will move up the plane.
(c) If m2 < m1 + (sinθ + µ cos θ), the body will move up the plane.
(d) If m2 < m1 (sinθ - µ cos θ), the body will move down the plane.
 View Answer
View Answer 
Ans. (b, d)
Solution.
Forces Acting on m1 on the Slope:
- Component of weight along the slope: m1gsinθ
- Normal force: N = m1gcosθ
- Frictional force: Ffriction = μN = μm1gcosθ
- Tension in the string: T (acts up the slope).
The net force on m1 is given by: Forces Acting on m2:
Forces Acting on m2:
The force on m2 is: Equation of Motion for the System:
Equation of Motion for the System:
The system will move when the forces on m1 and m2 are unbalanced. Considering the tension T and using Newton's second law for both masses, the condition for motion can be derived.
Case 1: Motion up the slope (m1 moves up)
For m1 to move up the slope, the force due to m2 must overcome the sum of the downhill forces acting on m1 . This gives:
m2g > m1g(sinθ + μcosθ)
Simplifying:
m2 > m1(sinθ + μcosθ)
Case 2: Motion down the slope (m1 moves down)
For m1 to move down the slope, the downhill forces acting on m1 must overcome the tension caused by m2. This gives:
m1g(sinθ − μcosθ) > m2g
Simplifying:
m2 < m1(sinθ − μcosθ)
Answer Choices:
(a) m2 > m1 sin θ : Incorrect, as friction is ignored in this condition.
(b) m2 > m1(sinθ+μcosθ): Correct, this is the condition for m1 to move up the plane.
(c) m2 < m1(sinθ + μcosθ): Incorrect, this condition doesn’t align with motion upward.
(d) m2 < m1(sinθ−μcosθ): Correct, this is the condition for m1 to move down the plane.
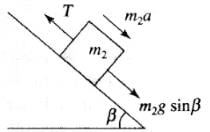
Q.13. In Fig, a body A of mass m slides on plane inclined at angle θ1 to the horizontal and µ1 is the coefficient of friction between A and the plane. A is connected by a light string passing over a frictionless pulley to another body B, also of mass m, sliding on a frictionless plane inclined at angle θ2 to the horizontal. Which of the following statements are true?(a) A will never move up the plane.
(b) A will just start moving up the plane when
(c) For A to move up the plane, θ2 must always be greater than θ1.
(d) B will always slide down with constant speed.
 View Answer
View Answer 
Ans. (b, c)
Solution.
| Condition | Free body diagrams |
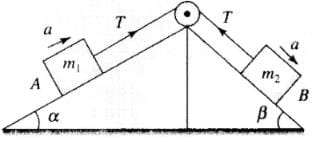 | 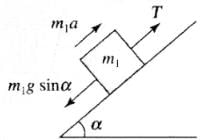 |
 | |
| Equation | Tension and acceleration |
| T - m1g sin α = m1a | 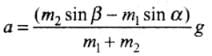 |
| m2a = m2g sin β - T | 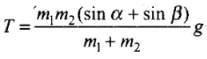 |
In this problem first we have to decide the direction of motion. Let block A moves up the plane friction force on A will be downward (along the plane) as shown.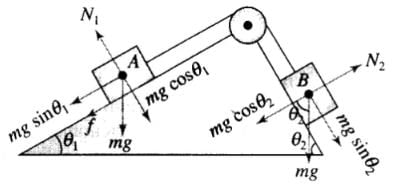

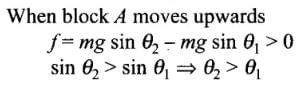
Q.14. Two billiard balls A and B, each of mass 50g and moving in opposite directions with speed of 5m s–1 each, collide and rebound with the same speed. If the collision lasts for 10–3 s, which of the following statements are true?
(a) The impulse imparted to each ball is 0.25 kg m s–1 and the force on each ball is 250 N.
(b) The impulse imparted to each ball is 0.25 kg m s–1 and the force exerted on each ball is 25 × 10–5 N.
(c) The impulse imparted to each ball is 0.5 Ns.
(d) The impulse and the force on each ball are equal in magnitude and opposite in direction.
 View Answer
View Answer 
Ans. (c, d)
Solution.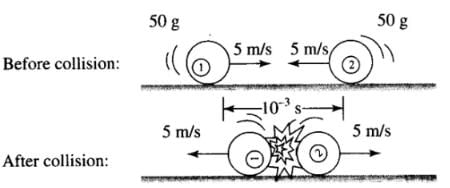
According to the problem, balls are identical.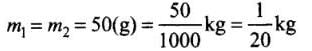
Initial velocity (u) = u1 = u2 = 5 m/s
Final velocity (v) = v1 = v2 = -5 m/s
Time duration of collision = 10-3s
Change in linear momentum = m(v - u)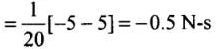
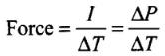

Impulse and force are opposite in directions.
Q.15. A body of mass 10kg is acted upon by two perpendicular forces, 6N and 8N. The resultant acceleration of the body is
(a) 1 m s–2 at an angle of tan-1 (4/3) w.r.t. 6N force.
(b) 0.2 m s–2 at an angle of tan-1 (4/3) w.r.t. 6N force.
(c) 1 m s–2 at an angle of tan-1 (3/4) w.r.t. 8N force.
(d) 0.2 m s–2 at an angle of tan-1 (3/4) w.r.t. 8N force.
 View Answer
View Answer 
Ans. (a, c)
Solution.
Recall the concept of resultant of two vectors, when they are perpendicular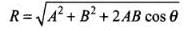
As they are perpendicular, cos 90° = 0
So resultant will be 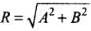
As shown in the diagram
According to the problem, mass = m = 10 kg
F1 = 6 N, F2 = 8 N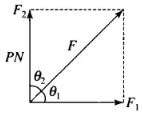
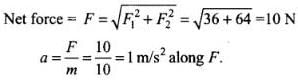
Let θ1 be the angle between F and F1.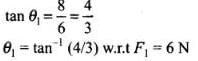
Let θ2 be angle between F and F2.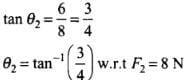
VERY SHORT ANSWER TYPE QUESTIONS
Q.1. A girl riding a bicycle along a straight road with a speed of 5 m s–1 throws a stone of mass 0.5 kg which has a speed of 15 m s–1 with respect to the ground along her direction of motion. The mass of the girl and bicycle is 50 kg. Does the speed of the bicycle change after the stone is thrown? What is the change in speed, if so?
 View Answer
View Answer 
Ans. Let m1 and m2 be the mass of girl with bicycle and stone respectively i.e. m1 = 50kg & m2 = 0.5kg
Also we have given u1 = 5m/s, u2 = 5m/s and v2 = 15 m/s and we have to find v1
As we know by law of conservation of momentum initial momentum (girl, bicycle, stone) = final momentum (cycle and girl) + stone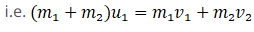
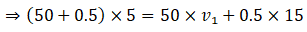
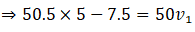
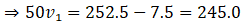
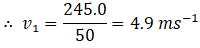
Therefore, the speed of cycle and girl decreased by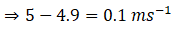
Q.2. A person of mass 50 kg stands on a weighing scale on a lift. If the lift is descending with a downward acceleration of 9 m s–2, what would be the reading of the weighing scale? (g = 10 m s–2)
 View Answer
View Answer 
Ans. Let the acceleration be ‘a’ when the lift is descending, then the apparent weight decreases on weighing scale
So W' = R
= mg - ma
= m(g - a)
Apparent weight due to reaction force by the lift on weighing scale will be
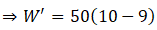
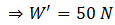
Reading of weighing scale = R/g = 50/10 = 5 kg
Q.3. The position time graph of a body of mass 2 kg is as given in Fig. What is the impulse on the body at t = 0 s and t = 4 s.
 View Answer
View Answer 
Ans. Here, m=2kg
As is clear from position time graph in
At t = 0 , x = 0 body is at rest . Therefore impulse of body (at t = 0) = 0
From t = 0 to t = 4 s position time graph of body is a st line with positive slope. The body moves with a unifrom velocity.
Beyoud t = 4 s position time graph is parallel to time axis Therefore, body comes to rest
Now initial vel of body (u) = tanθ = 3/4 m/s final vel of body
(v) = 0
∴ Impulse (at t = 4 s) = Change in momentum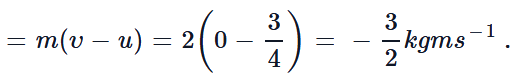
Q.4. A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
 View Answer
View Answer 
Ans. The phenomenon occurs due to inertia of motion, as described by Newton's First Law of Motion. Here's the explanation:
- When the car is moving, the person inside it is also moving at the same velocity as the car.
- When the brakes are suddenly applied, the car decelerates rapidly, coming to a stop.
- However, the person's body tends to maintain its state of motion (inertia) and continues to move forward with the original velocity of the car.
- Without a seatbelt to restrain him, the person moves forward and hits their head against the steering wheel.
This demonstrates how inertia resists changes in the state of motion, emphasizing the importance of wearing seatbelts to prevent such injuries.
Q.5. The velocity of a body of mass 2 kg as a function of t is given by 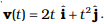 Find the momentum and the force acting on it, at time t = 2s.
Find the momentum and the force acting on it, at time t = 2s.
 View Answer
View Answer 
Ans. we have mass m = 2kg and 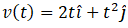

So momentum at 2 sec p (2) = mv (2)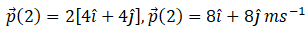
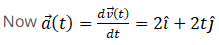
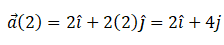
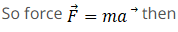
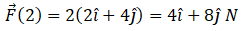
Hence momentum and force at 2 sec will be 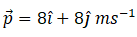 and
and 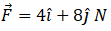 respectively.
respectively.
Q.6. A block placed on a rough horizontal surface is pulled by a horizontal force F. Let f be the force applied by the rough surface on the block. Plot a graph of f versus F.
 View Answer
View Answer 
Ans. Let f (frictional force) at y-axis and F at x-axis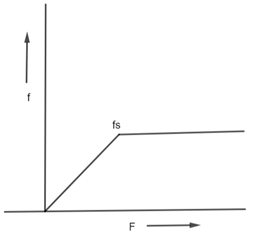 Now when a small force F1 is applied on a heavier box, this box does not move, at this state, force of friction f1 is equal to F1. Increasing force on box does not move till F = fs (the maximum static frictional or limiting force).
Now when a small force F1 is applied on a heavier box, this box does not move, at this state, force of friction f1 is equal to F1. Increasing force on box does not move till F = fs (the maximum static frictional or limiting force).
After force fs, the frictional force decrease i.e. less kinetic force Fk < fs is applied on body and it starts to move with less friction
In diagram A is equivalent to limiting frictional force and a B is equivalent to kinetic frictional force.
Q.7. Why are porcelain objects wrapped in paper or straw before packing for transportation?
 View Answer
View Answer 
Ans. Porcelain (or glass) objects are brittle in nature and can crack even small jerk on it. During transportation sudden jerks or even fall takes place.
When objects are packed in paper or straw etc., the objects takes more time to stop or change velocity during jerks (due to breaks, or uneven road) so acceleration (v - u)/t decreased. So the force on objects will be smaller and objects become safer.
Q.8. Why does a child feel more pain when she falls down on a hard cement floor, than when she falls on the soft muddy ground in the garden?
 View Answer
View Answer 
Ans. The effect of force F = ma. i.e., if the mass is constant for a system to decrease force, the ‘a’ should be decreased a = (v - u)/t initial and final velocity of falling body on a surface are u and zero. so it cannot be changed. If time during hitting is increased, the acceleration decreased and force will decrease.
On cemented hard floor the time to stop after fall on it is very-very small. But when she/he falls on soft ground of garden she/he sinks in ground and takes more time to stop hence smaller force or pain acts on her/him.
Q.9. A woman throws an object of mass 500 g with a speed of 25 m s1.
(a) What is the impulse imparted to the object?
(b) If the object hits a wall and rebounds with half the original speed, what is the change in momentum of the object?
 View Answer
View Answer 
Ans. (a) Mass of object m = 500 g = 0.5 kg
u = 0, v = 25 m/s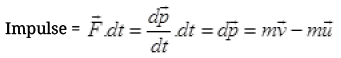
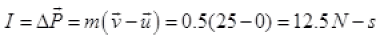
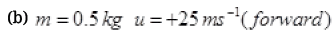
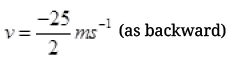
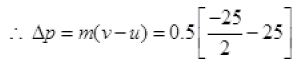
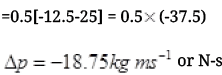
Hence, the 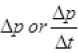 or force is opposite to the initial velocity of ball.
or force is opposite to the initial velocity of ball.
Q.10. Why are mountain roads generally made winding upwards rather than going straight up?
 View Answer
View Answer 
Ans. On an inclined plane force of friction on a body going upward is fs = μN cos θ where θ is angle of inclination of a plane with horizontal if θ is small, the force of friction is high and there is a less chance of skidding. The road straight up would have a larger angle and smaller would be the value of friction, hence more are the chances of skidding.
SHORT ANSWER TYPE QUESTIONS
Q.11. A mass of 2kg is suspended with thread AB (Fig). Thread CD of the same type is attached to the other end of 2 kg mass. Lower thread is pulled gradually, harder and harder in the downward directon so as to apply force on AB. Which of the threads will break and why?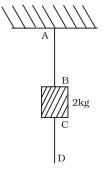
 View Answer
View Answer 
Ans. Forces Acting on Thread AB:
1. AB supports:
- The weight of the 2 kg mass (W = mg = 2kg . 9.8m/s2 = 19.6N).
- The additional tension due to the force applied by pulling thread CD downward.
Thus, the tension in thread AB increases as the force applied on CD increases.
Forces Acting on Thread CD:
CD experiences only the force applied downward, increasing gradually.
Breaking Scenario:
- If the applied force on CD is increased very slowly, the tension in AB will increase gradually because AB must support both the weight of the mass and the additional force applied through CD. In this case, AB will break first, as it experiences a greater total force.
- If the force on CD is applied suddenly and very hard, thread CD will likely break first due to the sudden jerk. This happens because the tension in CD can momentarily exceed its breaking point before AB has time to transmit the full force.
Conclusion
- If the force is applied gradually, thread AB will break because it bears the combined weight and applied force.
- If the force is applied suddenly, thread CD will break first due to the jerk effect.
Q.12. In the above given problem if the lower thread is pulled with a jerk, what happens?
 View Answer
View Answer 
Ans. Thread CD will break up if CD is pulled with the jerk because pull on thread CD is not transmitted from CD to AB by mass 2 kg due to its inertia of rest.
Q.13. Two masses of 5 kg and 3 kg are suspended with help of massless inextensible strings as shown in Fig. Calculate T1 and T2 when whole system is going upwards with acceleration = 2 m s2 (use g = 9.8 m s–2).
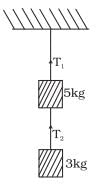
 View Answer
View Answer 
Ans. As the whole system is going up with acceleration = a= 2ms-2
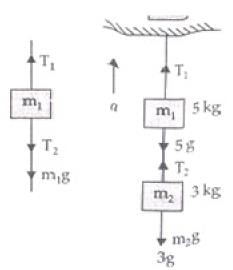 Tension in a string is equal and opposite in all parts of a string.
Tension in a string is equal and opposite in all parts of a string.
Forces on mass m1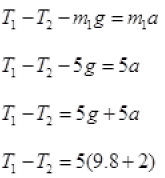
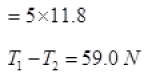
Forces on mass m2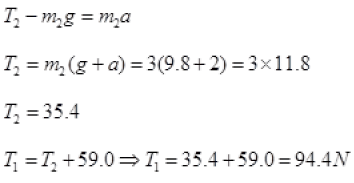
Q.14. Block A of weight 100 N rests on a frictionless inclined plane of slope angle 30° (Fig.). A flexible cord attached to A passes over a frictionless pulley and is connected to block B of weight W. Find the weight W for which the system is in equilibrium.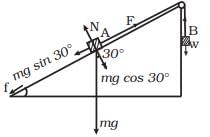
 View Answer
View Answer 
Ans. Step 1: Forces on Block A
Block A rests on a frictionless incline at an angle θ = 30∘. The forces acting on it are:
1. Its weight, WA = 100 N, which can be resolved into:
- Component along the plane: WA sin θ
- Component perpendicular to the plane: WA cos θ
2. Tension in the cord, T, which acts up the plane.
For equilibrium, the tension T must balance the component of the weight along the plane:
T = WAsinθ
Substitute WA = 100 N and sin 30° = 0.5:
T = 100⋅0.5 = 50N
Step 2: Forces on Block B
Block B is hanging vertically. The forces acting on it are:
- Its weight, WB =W, which acts downward.
- The tension in the cord, T, which acts upward.
For equilibrium:
T = W
Thus:
W = 50N
Q.15. A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is µ and the acceleration due to gravity is g, calculate the minimum force required to be applied by the finger to hold the block against the wall ?
 View Answer
View Answer 
Ans. Forces Acting on the Block:
Weight of the block: W=Mg, acting vertically downward due to gravity.
Frictional force: ffriction, acting upward and opposing the weight. The maximum frictional force is given by:
ffriction = μN
where N is the normal force exerted by the finger.
Normal force: N = F, the force applied by the finger perpendicular to the wall.
Condition for Equilibrium:
For the block to remain stationary, the upward frictional force must balance the downward weight:
ffriction = Mg
Substitute ffriction =μN and N = F:
μF=Mg
Rearranging for F: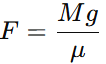
Q.16. A 100 kg gun fires a ball of 1kg horizontally from a cliff of height 500m. It falls on the ground at a distance of 400m from the bottom of the cliff. Find the recoil velocity of the gun. (acceleration due to gravity = 10 m s–2)
 View Answer
View Answer 
Ans. Given, the height of the cliff is,
Height of the cliff, h=500 m
Mass of the ball, m= 1 kg
Mass of the gun, M=100 kg
Range of the ball, R= 400 m
Acceleration due to gravity, g= 10 m s-2
Let the final velocity of the ball be u and the of the gun be v.
Now we know, time of flight is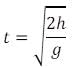
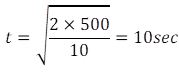
And range is given by:
R = ut
So, u=400/10 = 40 m s-2
Therefore, the velocity is: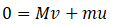
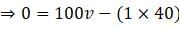
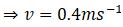
The recoil velocity of the gun is 0.4 m s-1.
Q.17. Figure shows (x, t), (y, t) diagram of a particle moving in 2-dimensionsIf the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.
 View Answer
View Answer 
Ans. From graph (a)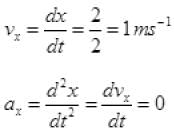
From figure (b) y = t2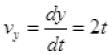
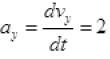
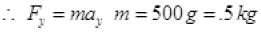
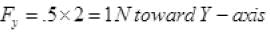
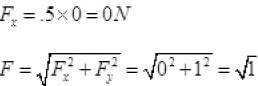
F = 1 N toward Y-axis.
Q.18. A person in an elevator accelerating upwards with an acceleration of 2 m s–2, tosses a coin vertically upwards with a speed of 20 m s1. After how much time will the coin fall back into his hand? (g = 10 m s–2)
 View Answer
View Answer 
Ans. Here, the initial velocity of the coin is, u = 20 m s1
And the acceleration of the elevator is, a = 2 m s-2
Here, let’s think this problem from the elevator reference frame. For the person inside the elevator going up with acceleration 2 m s-2 will experience a net acceleration of (g+a) which is 12 m s-2.
And as the coin return back to its original position (because we are in the elevator reference frame), the net displacement (s) is zero.
So we can use the laws of motion to solve the problem.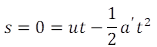
Here, a' = a + g = 12 m s-2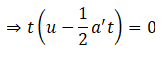
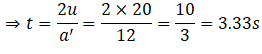
So the time of flight of the coin is 3.33 seconds.
LONG ANSWER TYPE QUESTIONS
Q.1. There are three forces F1, F2 and F3 acting on a body, all acting on a point P on the body. The body is found to move with uniform speed.
(a) Show that the forces are coplanar.
(b) Show that the torque acting on the body about any point due to these three forces is zero.
 View Answer
View Answer 
Ans. (a) We know force is a vector quantity. From the theory of planes, we know that two intersecting lines form a plane.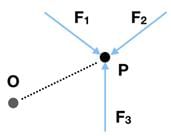 Let these lines be F1 and F2. This means that the vector sum, F1 + F2 is also on this plane.
Let these lines be F1 and F2. This means that the vector sum, F1 + F2 is also on this plane.
As the body is moving with uniform speed, the acceleration is zero. So the net of all forces is zero.
F1 + F2 + F3 = 0
So, F3 = - (F1 + F2)
This means even F3 lies on the same plane as F1 and F2.
Thus the forces are coplanar.
(b) As the sum of all forces are zero, the net torque in any direction is zero. For example, torque about “O” is
Τ = OP x (F1 + F2 + F3)
Τ = 0 as (F1 + F2 + F3) = 0
Hence, torque acting about any point is also zero.
Q.2 . When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
 View Answer
View Answer 
Ans. Step 1: Motion on a Smooth Inclined Plane (No Friction)
For a smooth inclined plane with angle θ=45∘:
- The acceleration of the body, asmooth, is due to gravity along the incline.
- Since there is no friction, asmooth = gsinθ.
For θ=45∘: 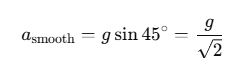
Using the second equation of motion, 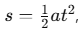 s is the distance traveled, a is the acceleration, and t is the time taken:
s is the distance traveled, a is the acceleration, and t is the time taken: 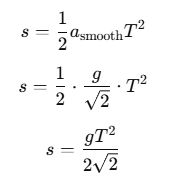
Step 2: Motion on a Rough Inclined Plane (With Friction)
Now, the same body slides down a rough inclined plane with the same angle θ=45∘ and the same distance s, but it takes a time pT where p>1.
Let μ be the coefficient of friction between the body and the rough plane. The frictional force f acting opposite to the motion is f=μN, where N is the normal force on the incline.
The normal force N on an incline is given by N=mgcosθ.
The net force acting on the body along the incline is:
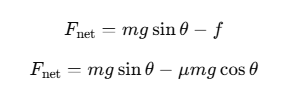
The net acceleration arough along the incline is then:
arough= g sinθ − μgcosθ
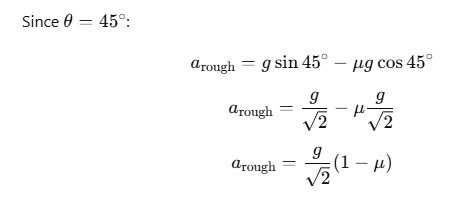
Using the same equation of motion s when the body takes time pT on the rough incline:
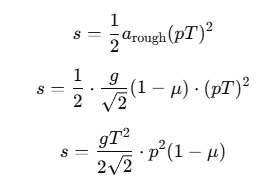
Step 3: Equate Distances for Both Cases
Since the distance s is the same in both cases, we can equate the expressions for s obtained from both scenarios:
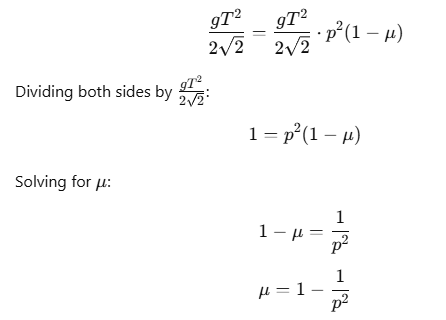
Q.3. Figure shows (vx,t),and(vy,t) diagrams for a body of unit mass. Find the force as a function of time.
 View Answer
View Answer 
Ans. Here, as the velocity shows different behavior at different times, we have to divide time into intervals to specify velocity.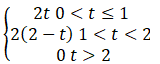
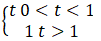
Now, we can differentiate velocity to calculate Forces(F).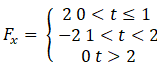
Hence, the total force is

Q.4. A racing car travels on a track (without banking) ABCDEFA (Fig.). ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The co-effecient of friction on the road is µ = 0.1. The maximum speed of the car is 50 m s–1. Find the minimum time for completing one round.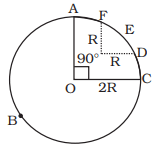
 View Answer
View Answer 
Ans. To find the total time, we find the time of each segments.
Segment: ABC
Here, the frictional force is
f = μmg
And the centripetal force is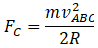
Therefore,
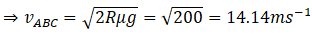
Segment:DEF
Again, the centripetal force is equal to friction.

Now, the time taken is distance/speed.
For ABC, the distance is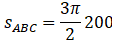
And for DEF we have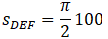
Therefore,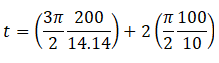 = 86.3
= 86.3
Hence the time taken is 86.3 seconds.
Q.5. The displacement vector of a particle of mass m is given by 
(a) Show that the trajectory is an ellipse.
(b) Show that Fr = −mω2r.
 View Answer
View Answer 
Ans. (a) Here, the x and y coordinates are
x = A cos ωt
y = B sin ωt
The equation of an ellipse is: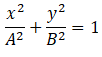
Substituting x and y, we find that LHS = RHS.
So the trajectory is an ellipse.
(b) To find force, we need to find acceleration.
This can be found by differentiating r two times with respect to t.
And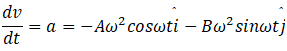
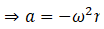
We know,
F = ma
⇒ F = -mrω2
Q.6. A cricket bowler releases the ball in two different ways
(a) Giving it only horizontal velocity, and
(b) Giving it horizontal velocity and a small downward velocity.
The speed vs at the time of release is the same. Both are released at a height H from the ground. Which one will have greater speed when the ball hits the ground? Neglect air resistance.
 View Answer
View Answer 
Ans. Case (a): Ball Released with Only Horizontal Velocity
In this case, the ball is released with only a horizontal velocity vs. There is no initial vertical velocity component. Let’s break down the motion into horizontal and vertical components:
Horizontal Motion:
- Horizontal velocity vx = vs (constant, as there’s no air resistance).
Vertical Motion:
Initial vertical velocity vy = 0.
Acceleration a=g (due to gravity).
Using the second equation of motion to find the time taken t to reach the ground:
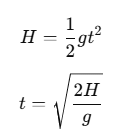
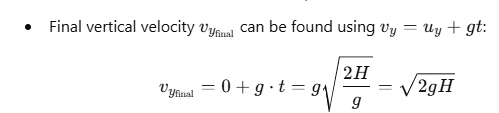
Case (b): Ball Released with Horizontal Velocity and Small Downward Velocity
In this case, the ball is released with a horizontal velocity vs and a small initial downward vertical velocity vy0.
Horizontal Motion:
- Horizontal velocity vx = vs (constant, as there’s no air resistance).
Vertical Motion:
- Initial vertical velocity vy0 (downward).
- Using the second equation of motion to find the time t it takes to reach the ground:

Solving for t is more complex in this case, but t will be slightly shorter than in Case (a) because of the initial downward velocity vy0.
Final Vertical Velocity:
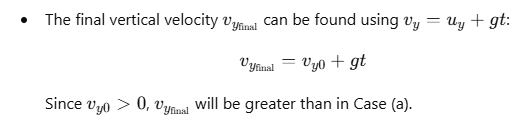
Final Speed at the Ground:

Conclusion
The ball in Case (b) (with both horizontal velocity and a small downward velocity) will have a greater speed when it hits the ground compared to the ball in Case (a). This is because the additional initial downward velocity increases the final vertical component of velocity, resulting in a higher overall speed upon impact.
Q.7. There are four forces acting at a point P produced by strings as shown in Fig. which is at rest. Find the forces F1 and F2 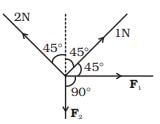
 View Answer
View Answer 
Ans. As the particle is rest or a = 0. So resultant force due to all forces will be zero.
∴ Net components along X and Y-axis will be zero.
Resolving all forces along X-axis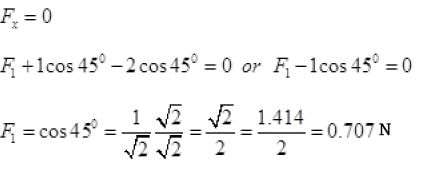
Resolving all forces along Y-axis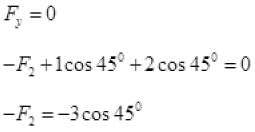

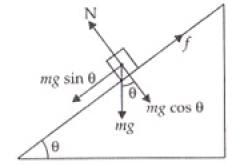
Q.8. A rectangular box lies on a rough inclined surface. The co-efficient of friction between the surface and the box is µ. Let the mass of the box be m.
(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane?
(b) What is the force acting on the box down the plane, if the angle of inclination of the plane is increased to α > θ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a?
 View Answer
View Answer 
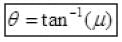
(b) If angle α > θ, the angle of inclination of the plane with horizontal it will slide down (f upward) as θ is the angle of repose. So net force downward
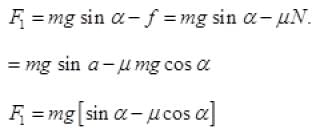
(c) To keep the box either stationary or just move it up with uniform velocity (1 =0) upward f downward)
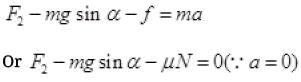
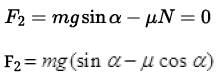
 (d) The force applied f.to move the box upward with acceleration a,
(d) The force applied f.to move the box upward with acceleration a,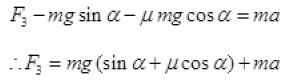
Q.9. A helicopter of mass 2000kg rises with a vertical acceleration of 15 m s–2. The total mass of the crew and passengers is 500 kg.
Give the magnitude and direction of the (g = 10 m s–2)
(a) Force on the floor of the helicopter by the crew and passengers.
(b) Action of the rotor of the helicopter on the surrounding air.
(c) Force on the helicopter due to the surrounding air.
 View Answer
View Answer 
Ans. (a) From the diagram, the force on the floor(F) is given by:
F - mg = ma
Where m is the mass of the crew and a is the upwards acceleration.
(b) Here, we have to consider all the weight if the system. The force due to rotor Fr is: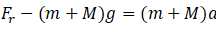
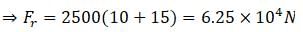
(c) This force is just the reaction force of Fr. So the force due to surrounding air is 6.25 x 104 N.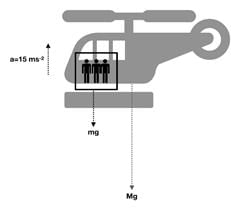
|
122 videos|481 docs|98 tests
|
FAQs on NCERT Exemplar: Laws of Motion - Physics Class 11 - NEET
| 1. What are Newton's three laws of motion? |  |
| 2. How do forces affect the motion of an object? |  |
| 3. What is the difference between mass and weight? |  |
| 4. Can you give examples of each of Newton's laws of motion? |  |
| 5. What is inertia and how does it relate to Newton's first law? |  |






















