NCERT Exemplar: Laws of Motion - 2 - NEET PDF Download
SHORT ANSWER TYPE QUESTIONS
Q.11. A mass of 2kg is suspended with thread AB (Fig). Thread CD of the same type is attached to the other end of 2 kg mass. Lower thread is pulled gradually, harder and harder in the downward directon so as to apply force on AB. Which of the threads will break and why?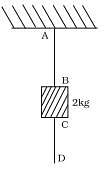
Ans. Thread AB will break. Force on CD is equal to the force (f) applied at D downward, but the force on thread AB is equal to the force F along with force due to mass 2 kg downward. so the force on AB is 2kg more than applied force at D.Hence the thread AB will break up.
Q.12. In the above given problem if the lower thread is pulled with a jerk, what happens?
Ans. Thread CD will break up if CD is pulled with the jerk because pull on thread CD is not transmitted from CD to AB by mass 2 kg due to its inertia of rest.
Q.13. Two masses of 5 kg and 3 kg are suspended with help of massless inextensible strings as shown in Fig. Calculate T1 and T2 when whole system is going upwards with acceleration = 2 m s2 (use g = 9.8 m s–2).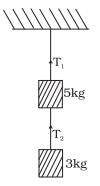
Ans. As the whole system is going up with acceleration = a= 2ms-2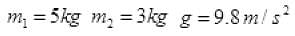
 Tension in a string is equal and opposite in all parts of a string.
Tension in a string is equal and opposite in all parts of a string.
Forces on mass m1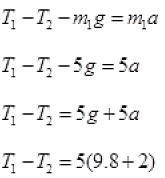

Forces on mass m2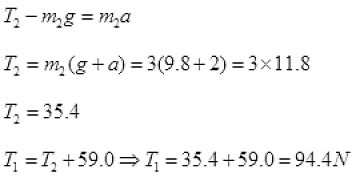
Q.14. Block A of weight 100 N rests on a frictionless inclined plane of slope angle 30° (Fig.). A flexible cord attached to A passes over a frictionless pulley and is connected to block B of weight W. Find the weight W for which the system is in equilibrium.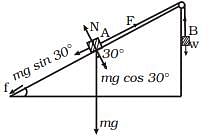 Ans. Main concept used: On balanced condition i.e., no motion then no frictional force or
Ans. Main concept used: On balanced condition i.e., no motion then no frictional force or
f = 0
Solution.
During equilibrium of A or B
mg sin30° = F
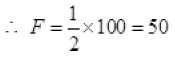
For B is at rest W = F = 50N.
Q.15. A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is µ and the acceleration due to gravity is g, calculate the minimum force required to be applied by the finger to hold the block against the wall ?
Ans. Let F force is applied by the finger on a body of mass M to hold rest against the wall. Under the balanced condition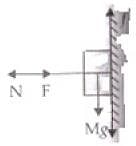
F = N
And f = Mg
⇒ μF = Mg
or 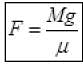 is the minimum force to hold the block against the wall at rest.
is the minimum force to hold the block against the wall at rest.
Q.16. A 100 kg gun fires a ball of 1kg horizontally from a cliff of height 500m. It falls on the ground at a distance of 400m from the bottom of the cliff. Find the recoil velocity of the gun. (acceleration due to gravity = 10 m s–2)
Ans. Given, the height of the cliff is,
Height of the cliff, h=500 m
Mass of the ball, m= 1 kg
Mass of the gun, M=100 kg
Range of the ball, R= 400 m
Acceleration due to gravity, g= 10 m s-2
Let the final velocity of the ball be u and the of the gun be v.
Now we know, time of flight is
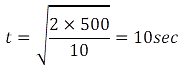
And range is given by:
R = ut
So, u=400/10 = 40 m s-2
Therefore, the velocity is: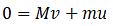


The recoil velocity of the gun is 0.4 m s-1.
Q.17. Figure shows (x, t), (y, t) diagram of a particle moving in 2-dimensions If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.
Ans. From graph (a)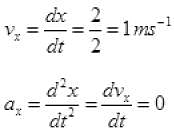
From figure (b) y = t2

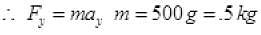
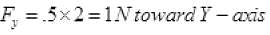
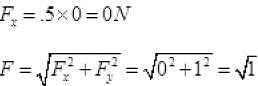
F = 1 N toward Y-axis.
Q.18. A person in an elevator accelerating upwards with an acceleration of 2 m s–2, tosses a coin vertically upwards with a speed of 20 m s1. After how much time will the coin fall back into his hand? (g = 10 m s–2)
Ans. Here, the initial velocity of the coin is, u = 20 m s1
And the acceleration of the elevator is, a = 2 m s-2
Here, let’s think this problem from the elevator reference frame. For the person inside the elevator going up with acceleration 2 m s-2 will experience a net acceleration of (g+a) which is 12 m s-2.
And as the coin return back to its original position (because we are in the elevator reference frame), the net displacement (s) is zero.
So we can use the laws of motion to solve the problem.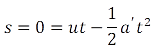
Here, a' = a + g = 12 m s-2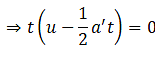
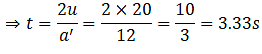
So the time of flight of the coin is 3.33 seconds.
LONG ANSWER TYPE QUESTIONS
Q.1. There are three forces F1, F2 and F3 acting on a body, all acting on a point P on the body. The body is found to move with uniform speed.
(a) Show that the forces are coplanar.
(b) Show that the torque acting on the body about any point due to these three forces is zero.
Ans. (a) We know force is a vector quantity. From the theory of planes, we know that two intersecting lines form a plane. Let these lines be F1 and F2. This means that the vector sum, F1 + F2 is also on this plane.
Let these lines be F1 and F2. This means that the vector sum, F1 + F2 is also on this plane.
As the body is moving with uniform speed, the acceleration is zero. So the net of all forces is zero.
F1 + F2 + F3 = 0
So, F3 = - (F1 + F2)
This means even F3 lies on the same plane as F1 and F2.
Thus the forces are coplanar.
(b) As the sum of all forces are zero, the net torque in any direction is zero. For example, torque about “O” is
Τ = OP x (F1 + F2 + F3)
Τ = 0 as (F1 + F2 + F3) = 0
Hence, torque acting about any point is also zero.
Q.2. When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane
Ans. General case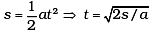
Smooth case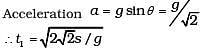
Rough case
Acceleration a = g sinθ − µg cosθ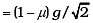
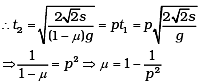
Q.3. Figure shows (vx,t),and(vy,t) diagrams for a body of unit mass. Find the force as a function of time.
 Ans. Here, as the velocity shows different behavior at different times, we have to divide time into intervals to specify velocity.
Ans. Here, as the velocity shows different behavior at different times, we have to divide time into intervals to specify velocity.
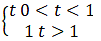
Now, we can differentiate velocity to calculate Forces(F).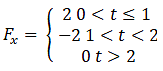
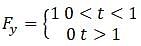
Hence, the total force is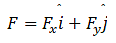

Q.4. A racing car travels on a track (without banking) ABCDEFA (Fig.). ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The co-effecient of friction on the road is µ = 0.1. The maximum speed of the car is 50 m s–1. Find the minimum time for completing one round.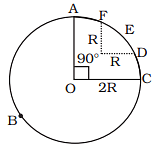 Ans. To find the total time, we find the time of each segments.
Ans. To find the total time, we find the time of each segments.
Segment: ABC
Here, the frictional force is
f = μmg
And the centripetal force is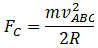
Therefore,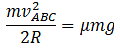
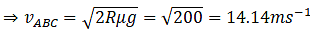
Segment:DEF
Again, the centripetal force is equal to friction.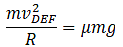
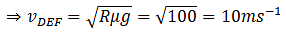
Now, the time taken is distance/speed.
For ABC, the distance is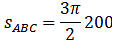
And for DEF we have
Therefore,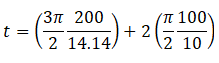 = 86.3
= 86.3
Hence the time taken is 86.3 seconds.
Q.5. The displacement vector of a particle of mass m is given by 
(a) Show that the trajectory is an ellipse.
(b) Show that Fr = −mω2r.
Ans. (a) Here, the x and y coordinates are
x = A cos ωt
y = B sin ωt
The equation of an ellipse is:
Substituting x and y, we find that LHS = RHS.
So the trajectory is an ellipse.
(b) To find force, we need to find acceleration.
This can be found by differentiating r two times with respect to t.
And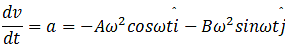

We know,
F = ma
⇒ F = -mrω2
Q.6. A cricket bowler releases the ball in two different ways
(a) Giving it only horizontal velocity, and
(b) Giving it horizontal velocity and a small downward velocity.
The speed vs at the time of release is the same. Both are released at a height H from the ground. Which one will have greater speed when the ball hits the ground? Neglect air resistance.
Ans.

For (b) also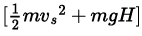 is the total energy of the ball when it hits the ground
is the total energy of the ball when it hits the ground
So the speed would be the same for both (a) and (b).
Q.7. There are four forces acting at a point P produced by strings as shown in Fig. which is at rest. Find the forces F1 and F2 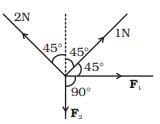 Ans. As the particle is rest or a = 0. So resultant force due to all forces will be zero.
Ans. As the particle is rest or a = 0. So resultant force due to all forces will be zero.
∴ Net components along X and Y-axis will be zero.
Resolving all forces along X-axis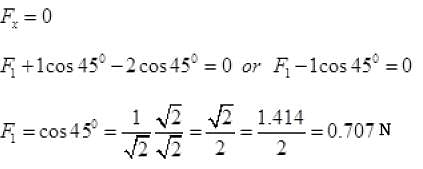
Resolving all forces along Y-axis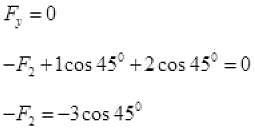
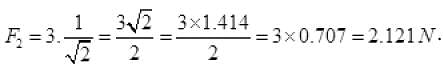
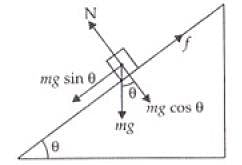
Q.8. A rectangular box lies on a rough inclined surface. The co-efficient of friction between the surface and the box is µ. Let the mass of the box be m.
(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane?
(b) What is the force acting on the box down the plane, if the angle of inclination of the plane is increased to α > θ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a?
Ans. (a) As the box just start to slide down the plane then μ = tan θ (by angle of repose)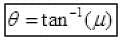
(b) If angle α > θ, the angle of inclination of the plane with horizontal it will slide down (f upward) as θ is the angle of repose. So net force downward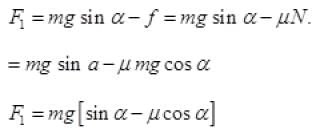
(c) To keep the box either stationary or just move it up with uniform velocity (1 =0) upward f downward)

 (d) The force applied f.to move the box upward with acceleration a,
(d) The force applied f.to move the box upward with acceleration a,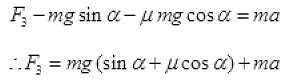
Q.9. A helicopter of mass 2000kg rises with a vertical acceleration of 15 m s–2. The total mass of the crew and passengers is 500 kg.
Give the magnitude and direction of the (g = 10 m s–2)
(a) Force on the floor of the helicopter by the crew and passengers.
(b) Action of the rotor of the helicopter on the surrounding air.
(c) Force on the helicopter due to the surrounding air.
Ans. (a) From the diagram, the force on the floor(F) is given by:
F - mg = ma
Where m is the mass of the crew and a is the upwards acceleration.
(b) Here, we have to consider all the weight if the system. The force due to rotor Fr is: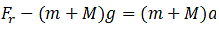
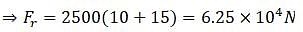
(c) This force is just the reaction force of Fr. So the force due to surrounding air is 6.25 x 104 N.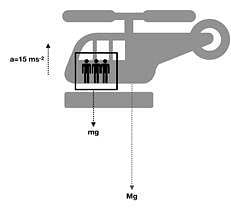
FAQs on NCERT Exemplar: Laws of Motion - 2 - NEET
| 1. What are the three laws of motion? |  |
| 2. How do the laws of motion apply to everyday life? |  |
| 3. What is inertia? |  |
| 4. What is the relationship between force, mass, and acceleration? |  |
| 5. Can you provide an example that illustrates Newton's third law of motion? |  |

|
Explore Courses for NEET exam
|

|

















