NCERT Exemplar: Thermal Properties of Matter | Physics Class 11 - NEET PDF Download
MULTIPLE CHOICE QUESTIONS I
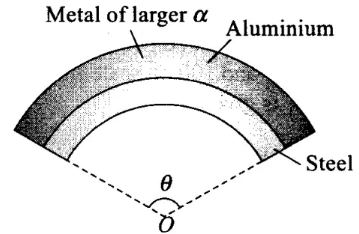
Q.1. A bimetallic strip is made of aluminium and steel (αAl >αsteel). On heating, the strip will
(a) Remain straight.
(b) Get twisted.
(c) Will bend with aluminium on concave side.
(d) Will bend with steel on concave side.
Ans. (d)
Solution.
Bi-metallic strip: Two strips of equal lengths but of different materials (different coefficient of linear expansion) when join together, it is called “bi-metallic strip”, and can be used in thermostat to break or make electrical contact. This strip has the characteristic property of bending on heating due to unequal linear expansion of the two metal. The strip will bend with metal of greater a on outer side, i.e. convex side.
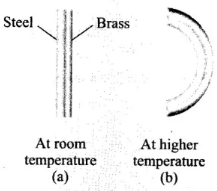
On heating, the metallic strip with higher coefficient of linear expansion (∝Al) will expand more.
According to the question, ∝AI > ∝steel, so aluminum will expand more. So, it should have larger radius of curvature. Hence, aluminium will be on convex side. The metal of smaller ∝ (i.e., steel) bends on inner side, i.e., concave side.
Q.2. A uniform metallic rod rotates about its perpendicular bisector with constant angular speed. If it is heated uniformly to raise its temperature slightly
(a) Its speed of rotation increases.
(b) Its speed of rotation decreases.
(c) Its speed of rotation remains same.
(d) Its speed increases because its moment of inertia increases.
Ans. (b)
Solution.
When the rod is heated uniformly to raise its temperature slightly, it expands. So, moment of inertia of the rod will increase.
Moment of inertia of a uniform rod about its perpendicular bisector
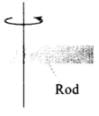
Moment of inertia of a uniform rod about its perpendicular bisector,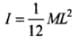
ΔT = Increase in the temperature of the rod.
∴ Changed length, L' = L(1 + αΔT) ...(i)
∴ New moment of inertia of rod,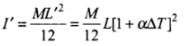
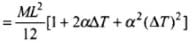 [Using (i)]
[Using (i)]
∴ I' = I[ 1 + 2αΔT ] (∵ α2(ΔT)2 is very small)
If the temperature increases, moment of inertia will increase.
No external torque is acting on the system, so angular momentum should be conserved.
L = Angular momentum = Iω = constant
⇒ I'ω' = Iω
where, I = initial M.I. of rod before heating
ω = Initial angular velocity
I' = Final M.I. after heating
ω' = Final angular velocity after heating
Due to expansion of the rod I' > I.
⇒ 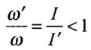
⇒ ω' < ω
So, angular velocity (speed of rotation) decreases.
Q.3. The graph between two temperature scales A and B is shown in Figure. Between upper fixed point and lower fixed point there are 150 equal division on scale A and 100 on scale B.
The relationship for conversion between the two scales is given by

(a) 
(b) 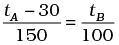
(c) 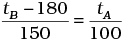
(d) 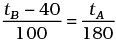
Ans. (b)
Solution.
It is clear from graph in tA scale lower fixed point (LEP) is 30° and upper fixed point (UFP) is 180°. Similarly in scale B, UFP = 100° and LFP= 0°.
Hence formula 

Or 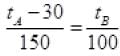
Q.4. An aluminium sphere is dipped into water. Which of the following is true?
(a) Buoyancy will be less in water at 0°C than that in water at 4°C.
(b) Buoyancy will be more in water at 0°C than that in water at 4°C.
(c) Buoyancy in water at 0°C will be same as that in water at 4°C.
(d) Buoyancy may be more or less in water at 4°C depending on the radius of the sphere.
Ans. (a)
Solution.
Liquids generally increase in volume with increasing temperature but in case of water, it expands on heating if its temperature is greater than 4°C. The density of water reaches a maximum value of 1.000 g/cm3 at 4°C.
This behaviour of water in the range from 0°C to 4°C is called anomalous expansion.
Let volume of the sphere be V and ρ be its density, then we can write buoyant force at 0°C.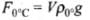 (ρ0° = density at 0°C)
(ρ0° = density at 0°C)
Buoyancy at 4°C
⇒ 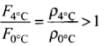

⇒ 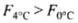
Hence, buoyancy will be less in water at 0°C than that in water at 4°C.
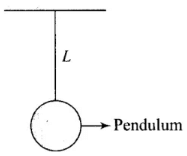
Q.5. As the temperature is increased, the time period of a pendulum
(a) Increases as its effective length increases even though its centre of mass still remains at the centre of the bob.
(b) Decreases as its effective length increases even though its centre of mass still remains at the centre of the bob.
(c) Increases as its effective length increases due to shifting of centre of mass below the centre of the bob.
(d) Decreases as its effective length remains same but the centre of mass shifts above the centre of the bob.
Ans. (a)
Solution.
A pendulum clock keeps proper time at temperature θ0. If temperature is increased to θ (>θ0), then due to linear expansion, length of pendulum increases and hence its time period will increase
Let T = 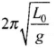 at temperature θ0 and
at temperature θ0 and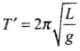 at temperature θ.
at temperature θ.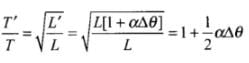
Therefore change (loss or gain) in time per unit time lapsed is 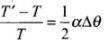
Fractional change in time period 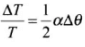
So, as the temperature increases, length of pendulum increases and hence time period of pendulum increases. Due to increment in its time period, a pendulum clock becomes slow in summer and will lose time.
Q.6. Heat is associated with
(a) Kinetic energy of random motion of molecules.
(b) Kinetic energy of orderly motion of molecules.
(c) Total kinetic energy of random and orderly motion of molecules.
(d) Kinetic energy of random motion in some cases and kinetic energy of orderly motion in other.
Ans. (a)
Solution.
We know that as the temperature increases vibration of molecules about their mean position increases. Hence the Kinetic energy associated with random motion of molecule increases.
Q.7. The radius of a metal sphere at room temperature T is R, and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature ∆T so that its new temperature is T +∆T. The increase in the volume of the sphere is approximately
(a) 2π R α ∆T
(b) π R2 α ∆T
(c) 4π R3 α ∆T/3
(d) 4π R3 α ∆T
Ans. (d)
Solution.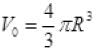
Coefficient of linear expansion is α
Coefficient of cubical expansion = 3α = γ
verifies option (d).
Q.8. A sphere, a cube and a thin circular plate, all of same material and same mass are initially heated to same high temperature.
(a) Plate will cool fastest and cube the slowest
(b) Sphere will cool fastest and cube the slowest
(c) Plate will cool fastest and sphere the slowest
(d) Cube will cool fastest and plate the slowest
Ans. (c)
Solution.
loss of heat on cooling is directly proportional to the following factors
(i) temperature difference between body and surrounding
(ii) surface area exposed to surrounding
(iii) material of object
We know that surface area of sphere is minimum and of circular plate is maximum. So sphere cool slowest and circular plate fastest.
MULTIPLE CHOICE QUESTIONS II
Q.9. Mark the correct options:
(a) A system X is in thermal equilibrium with Y but not with Z. System Y and Z may be in thermal equilibrium with each other.
(b) A system X is in thermal equilibrium with Y but not with Z. Systems Y and Z are not in thermal equilibrium with each other.
(c) A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z must be in thermal equilibrium with each other.
(d) A system X is neither in thermal equilibrium with Y nor with Z. The system Y and Z may be in thermal equilibrium with each other.
Ans. (b, d)
Solution.
Two bodies are said to be in thermal equilibrium with each other, when no heat flows from one body to the other. That is when both the bodies are at the same temperature.
According to the problem,
(b) If two systems X and Y are in thermal equilibrium, i.e., Tx = Ty and x is not in thermal equilibrium with z,
i.e., Tx ≠ Tz
then clearly, Ty ≠ Tz
Hence, y and z are not in thermal equilibrium.
(d) If X is not in thermal equilibrium with Y, i.e, Tx ≠ Ty and also X is not in thermal equilibrium with Y, i.e., Tx ≠ Tz
Then we cannot say about equilibrium of Y and Z, they may or may not be in equilibrium.
Q.10. ‘Gulab Jamuns’ (assumed to be spherical) are to be heated in an oven. They are available in two sizes, one twice bigger (in radius) than the other. Pizzas (assumed to be discs) are also to be heated in oven. They are also in two sizes, one twice big (in radius) than the other. All four are put together to be heated to oven temperature. Choose the correct option from the following:
(a) Both size gulab jamuns will get heated in the same time.
(b) Smaller gulab jamuns are heated before bigger ones.
(c) Smaller pizzas are heated before bigger ones.
(d) Bigger pizzas are heated before smaller ones.
Ans. (b, c)
Solution.
Between these four which has the least surface area will be heated first because of less heat radiation. So, smaller gulab jamuns are having least surface area, hence they will be heated first.
Similarly, smaller pizzas are heated before bigger ones because they are of small surface areas.
Q.11. Refer to the plot of temperature versus time (Figure.) showing the changes in the state of ice on heating (not to scale).
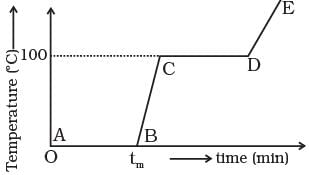
Which of the following is correct?
(a) The region AB represents ice and water in thermal equilibrium.
(b) At B water starts boiling.
(c) At C all the water gets converted into steam.
(d) C to D represents water and steam in equilibrium at boiling point.
Ans. (a, d)
Solution.
During phase change process, temperature of the system remains constant.
(a) In region AB, a phase change takes place, heat is supplied and ice melts but temperature of the system is 0°C. it remains constant during process. The heat supplied is used to break bonding between molecules.
(b) In region CD, again a phase change takes place from a liquid to a vapour state during which temperature remains constant. It shows water and steam are in equilibrium at boiling point.
Q.12. A glass full of hot milk is poured on the table. It begins to cool gradually. Which of the following is correct?
(a) The rate of cooling is constant till milk attains the temperature of the surrounding.
(b) The temperature of milk falls off exponentially with time .
(c) While cooling, there is a flow of heat from milk to the surrounding as well as from surrounding to the milk but the net flow of heat is from milk to the surrounding and that is why it cools.
(d) All three phenomenon, conduction, convection and radiation are responsible for the loss of heat from milk to the surroundings.
Ans. (b, c, d)
Solution.
When hot milk spread on the table heat is transferred to the surroundings by conduction, convection and radiation. Because the surface area of poured milk on a table is more than the surface area of milk filled in a glass. Hence, its temperature falls off exponentially according to Newton’s law of cooling. Heat also will be transferred from surroundings to the milk but will be lesser than that of transferred from milk to the surroundings. So, option (b), (c) and (d) are correct.
VERY SHORT ANSWER TYPE QUESTIONS
Q.1. Is the bulb of a thermometer made of diathermic or adiabatic wall?
Ans. The bulb of a thermometer is made up of diathermic wall because diathermic walls allow exchange of heat energy between two systems but adiabatic walls do not. So it receives heat from the body to measure the temperature of body.
Q.2. A student records the initial length l, change in temperature ∆T and change in length ∆l of a rod as follows:
| S.No. | l(m) | ΔT(C) | Δl(m) |
| 1. | 2 | 10 | 4 x 10-4 |
| 2. | 1 | 10 | 4 x 10-4 |
| 3. | 2 | 20 | 2 x 10-4 |
| 4. | 3 | 10 | 6 x 10-4 |
If the first observation is correct, what can you say about observations 2, 3 and 4.
Ans. If the first observation is correct, hence from the 1st observation we get the coefficient of linear expansion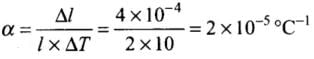
For 2nd observation, Δl = αlΔT
= 2 x 10-5 x 1 x 10
= 2 x 10-4 m ≠ 4 x 10-4 m
which is incorrect.
For 3rd observation, Δl = αlΔT
= 2 x 10-5 x 2 x 20
= 8 x 10-4 m ≠ 2 x 10-4 m
which is incorrect.
For 4th observation, ∆l = ∝l∆T
= 2 x 10-5 x 3 x 10 = 6 x 10-4 m [i.e., observed value is correct]
Q.3. Why does a metal bar appear hotter than a wooden bar at the same temperature? Equivalently it also appears cooler than wooden bar if they are both colder than room temperature.
Ans. Kirchhoffs Law:
The ratio of emissive power to absorptive power is same for all surfaces at the same temperature and is equal to the emissive power of a perfectly black body at that temperature.
Thus if apractical and Epractical represent the absorptive and emissive power of a given surface, while ablack and Eblack for a perfectly black body, then according to law 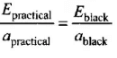
But for a perfectly black body ablack = 1, so 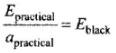
If emissive and absorptive powers are considered for a particular wavelength λ, 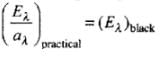
Now since (Eλ)Black is constant at a given temperature, according to this law if a surface is a good absorber of a particular wavelength it is also a good emitter of that wavelength.
This in turn implies that a good absorber is a good emitter (or radiator).
The conductivities of metals are very high compared to wood. Due to difference in conductivity, if one touch the hot metal with a finger, heat from the surrounding flows faster to the finger from metals and so one feels the heat.
Similarly, when one touches a cold metal the heat from the finger flows away to the surroundings faster. So we can say that a good radiator can be a good absorber.
Q.4. Calculate the temperature which has same numeral value on celsius and Fahrenheit scale.
Ans. To construct a scale of temperature, two fixed points are taken. First fixed point is the freezing point of water, it is called lower fixed point. The second fixed point is the boiling point of water, it is called upper fixed point. Temperature on one scale can be converted into other scale by using the following identity. Constant for all scales
Constant for all scales
Let T be the value of temperature having same value of Celsius and Fahrenheit scale, i.e. F = C = T
⇒ 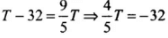
⇒mT = -40°C = -40°F
Q.5. These days people use steel utensils with copper bottom. This is supposed to be good for uniform heating of food. Explain this effect using the fact that copper is the better conductor.
Ans. As the copper has higher conductivity and low specific heat as compares of steel. So copper base transfer heat quickly to food from bottom and also need low quantity of heat due to lower specific heat as compared to steel.
So copper base supply quick and larger heat from burner to food in utensil.
SHORT ANSWER TYPE QUESTIONS
Q.1. Find out the increase in moment of inertia I of a uniform rod (coefficient of linear expansion α) about its perpendicular bisector when its temperature is slightly increased by ∆T.
Ans. Moment of inertia of a uniform rod of mass M and length l about its perpendicular bisector

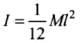
Increase in length of the rod when temperature is increased by Δt, is given by
L' = L(1 + αΔT)
∴ New moment of inertia of the rod
∴ As change in length Δl is very small, therefore neglecting (Δl)2
(∵ α2(ΔT)2 is very small) we get
I' = I[1 + 2αΔT]
∴ Increase in moment of inertia
= I' - I = I[1 + 2αΔT] - I = 2αIΔT
Q.2. During summers in India, one of the common practice to keep cool is to make ice balls of crushed ice, dip it in flavoured sugar syrup and sip it. For this a stick is inserted into crushed ice and is squeezed in the palm to make it into the ball. Equivalently in winter, in those areas where it snows, people make snow balls and throw around. Explain the formation of ball out of crushed ice or snow in the light of P–T diagram of water.
Ans. Refer to the P.T diagram of water and double headed arrow. Increasing pressure at 0°C and 1 atm takes ice into liquid state and decreasing pressure in liquid state at 0°C and 1 atm takes water to ice state.
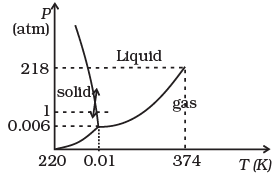
When crushed ice is squeezed, some of it melts, filling up gap between ice flakes. Upon releasing pressure, this water freezes binding all ice flakes making the ball more stable.
Q.3. 100 g of water is supercooled to –10°C. At this point, due to some disturbance mechanised or otherwise some of it suddenly freezes to ice. What will be the temperature of the resultant mixture and how much mass would freeze?
[Sw = 1cal/g/°C and Lwfusion = 80cal/g]
Ans. According to the problem, mass of water (m) = 100 g
Change in temperature ΔT = 0 - (-10) = 10°C
Specific heat of water(Sw) = 1 cal/g/°C
Latent heat of fusion of water Lwfusion = 80 cal/g
Amount of heat required to change the temperature of 100 g of water at -10°C to 0°C,
Q = mSwΔT
= 100 x 1 x [0 -(-10)] = 1000 cal
Let m gram of ice be melted.
∴ Q = mL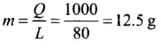
or
As small mass of ice is melted, thus the temperature of the resultant mixture will remain 0°C which contains 12.5 g of ice and 87.5 g of water.
Q.4. One day in the morning, Ramesh filled up 1/3 bucket of hot water from geyser, to take bath. Remaining 2/3 was to be filled by cold water (at room temperature) to bring mixture to a comfortable temperature. Suddenly Ramesh had to attend to something which would take some times, say 5-10 minutes before he could take bath. Now he had two options: (i) fill the remaining bucket completely by cold water and then attend to the work, (ii) first attend to the work and fill the remaining bucket just before taking bath. Which option do you think would have kept water warmer? Explain.
Ans. The first option would have kept water warmer because according to Newton’s law of cooling, the rate of loss of heat is directly proportional to the difference of temperature of the body and the surrounding and in the first case the temperature difference is less, so rate of loss of heat will be less.
LONG ANSWER TYPE QUESTIONS
Q.1. We would like to prepare a scale whose length does not change with temperature. It is proposed to prepare a unit scale of this type whose length remains, say 10 cm. We can use a bimetallic strip made of brass and iron each of different length whose length (both components) would change in such a way that difference between their lengths remain constant. If αiron = 1.2 x 10-5/ K and αbrass = 1.8 x 10-5/K, what should we take as length of each strip?
Ans. According to the problem, L1-Lb = 10 cm where,
L1 = length of iron scale
Lb = Length of brass scale
This condition is possible if change in length both the rods is remain same at all temperatures.
Change in length of iron rod,
ΔL = α1L1ΔT
Change in length of brass rod,
ΔL = αBLBΔT
As the change will equal in both the rods, so
α1L1ΔT = αBLBΔT
⇒ 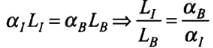
Here,
∴ 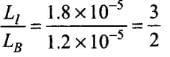
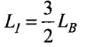
As, L1 - LB = 10 cm
∴ 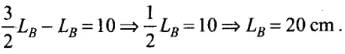
Q.2. We would like to make a vessel whose volume does not change with temperature (take a hint from the problem above). We can use brass and iron ( βvbrass = 6 × 10–5/K and βviron = 3.55 ×10–5/ K) to create a volume of 100 cc. How do you think you can achieve this.
Ans. Iron vessel with a brass rod inside
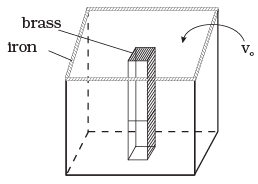
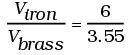
Viron - Vbrass = 100cc = V0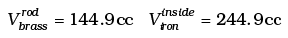
Q.3. Calculate the stress developed inside a tooth cavity filled with copper when hot tea at temperature of 57°C is drunk. You can take body (tooth) temperature to be 37°C and α = 1.7 × 10-5/°C, bulk modulus for copper = 140 × 109 N/m2.
Ans. Stress = K × strain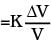
=K(3α)∆t
= 140 x 109 x 3 x 1.7 x 10-5 x 20
= 1.428 ×108 N/m2
This is about 103 times atmospheric pressure.
Q.4. A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (Figure). On a summer day due to rise in temperature by 20°C , it is deformed as shown in figure.

Find x (displacement of the centre) if αsteel = 1.2 × 10-5/°C.
Ans. Diagram shows the deformation of a railway track due to rise in temperature.
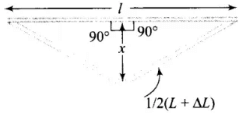
Applying Pythagoras theorem in right angled triangle,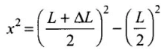
⇒ 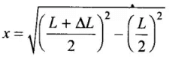
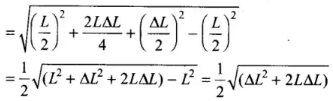
As increase in length ΔL is very small, therefore, neglecting (ΔL)2, we get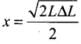 ...(i)
...(i)
But ΔL = LαΔt ...(ii)
According to the problem, L = 10 m,
α = 1.2 x 10-5 °C-1, ΔT = 20°C
Substituting value of ΔL in Eq. (i) from Eq. (ii)
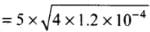
= 5 x 2 x 1.1 x 10-2
= 0.11 m = 11 cm
Q.5. A thin rod having length L0 at 0°C and coefficient of linear expansion α has its two ends maintained at temperatures θ1 and θ2, respectively. Find its new length.
Ans. As the temperature of rod varies from θ1 to θ2 from one end to another. So mean temperature of rod 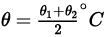
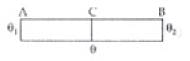
So rate of flow of heat from A to C to B are equal
∵ θ1 > θ > θ2
∴ 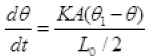
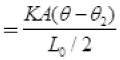
K is coefficient of thermal conductivity
∴ θ1 - θ = θ - θ2
L = L0(1 + αθ) = 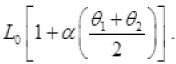
Q.6. According to Stefan’s law of radiation, a black body radiates energy σT4 from its unit surface area every second where T is the surface temperature of the black body and σ = 5.67 × 10-8 W/ m2K4 is known as Stefan’s constant. A nuclear weapon may be thought of as a ball of radius 0.5 m. When detonated, it reaches temperature of 106K and can be treated as a black body.
(a) Estimate the power it radiates.
(b) If surrounding has water at 30°C, how much water can 10% of the energy produced evaporate in 1 s?
[Sw = 4186.0 J/kg K and Lv = 22.6×105J/kg]
(c) If all this energy U is in the form of radiation, corresponding momentum is p = U/c. How much momentum per unit time does it impart on unit area at a distance of 1 km?
Ans. (a) E = σT4 per second per sq. m
Total E = radiated from all surface area A per sec will be power radiated by nuclear weapon
P = σAT4
σ = 5.67 x 10-8 W/m2/K4, R = 0.5m, T = 106 K
P = 5.67 x 10-8 x ( 4 x πR2) (106)4
= 5.67 x 4 x 3.14 x .5 x .5 x 10-8 x 1024
= 5.67 x 3.14 x 1024-8 x 1.00
P ≅ 18 x 1016 Watt = 1.8 x 1017 J/s
(b) ∴ P = 18 x 1016 watt
10% of this power is required to evaporate water
E = (10/100) x 18 x 1016 Watt = 1.8 x 1016 j/s
Energy required by m kg water at 30°C to evaporate 100°C.
E required to heat up water from 30°C to 100°C
+E required to evaporate water into vapour
= mSw(T2 - T1) + mL = m(Sw(T2 - T1) + L)
1.8 x 1016 = m[4180(100-30) + 22.6 x 105]
= m[4186 x 70 + 22.6 x 105]
m(2.93020 + 22.6) x 105 = 1.8 x 1016
m = 25.5 x 105 = 1.8 x 1016
m = 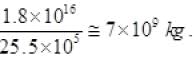
(c) Momentum per unit time p’ 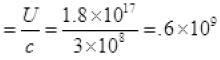
From (I) P' = 6 x 108 Kgms-2
P per unit time per unit at a distance 1 km 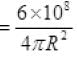
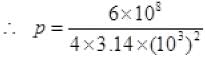
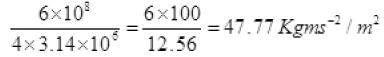
P per sec at 1 km away on m2 = 47.8 N/m2.
|
97 videos|378 docs|103 tests
|
FAQs on NCERT Exemplar: Thermal Properties of Matter - Physics Class 11 - NEET
| 1. What are the different units used to measure thermal conductivity? |  |
| 2. How does thermal expansion affect the dimensions of an object? |  |
| 3. What is specific heat capacity and how is it related to thermal properties? |  |
| 4. How does thermal conductivity affect the rate of heat transfer in different materials? |  |
| 5. What is the significance of the coefficient of linear expansion in thermal properties? |  |

|
Explore Courses for NEET exam
|

|

















