NCERT Exemplar: Thermodynamics - 2 | NCERT Exemplar & Revision Notes for NEET PDF Download
SHORT ANSWER TYPE QUESTION
Q.34. The molar enthalpy of vapourisation of acetone is less than that of water. Why?
Ans. Molar enthalpy of vapourisation is more for water due to hydrogen bonding between water molecules.
Q.35. Which quantity out of ∆rG and ∆rGΘ will be zero at equilibrium?
Ans. Gibbs energy for a reaction in which all reactants and products are in standard state. ΔrGΘ is related to the equilibrium constant of the reaction as follows
ΔrG = ArGΘ + RT In K
At equilibrium, 0 = ΔrGΘ + RT In A– (ΔrG = 0) or ΔrG° = -RT lnK
ΔrG° = 0 when K= 1
For all other values of K, ArG° will be non-zero.
Q.36. Predict the change in internal energy for an isolated system at constant volume.
Ans. For an isolated system w = 0, q = 0
Since ΔU= q + w = 0 + 0 = 0, ΔU= 0
Q.37. Although heat is a path function but heat absorbed by the system under certain specific conditions is independent of path. What are those conditions? Explain.
Ans.
At constant volume
q = ΔU + (-w)
-w = pΔ q = AU + pΔV
ΔV = 0 (at constant volume)
Hence,
qv = ΔU + 0 = ΔU= change in internal energy At constant pressure,
qp = AU + pΔV
Since ΔU + pΔV=ΔH
⇒ qp = ΔH change in enthalpy
Hence, at constant volume and at constant pressure, heat change is a state function because it is equal to ΔU and ΔH respectively which are state functions.
Q.38. Expansion of a gas in vacuum is called free expansion. Calculate the work done and the change in internal energy when 1 litre of ideal gas expands isothermally into vacuum until its total volume is 5 litre?
Ans. During free expansion, external pressure is zero, so Work done, w = -pextΔV
= -0(5 – 1) = 0
Since the gas is expanding isothermally, therefore, q = 0
ΔU = q + w = 0 + 0 = 0
Q.39. Heat capacity (Cp) is an extensive property but specific heat (c) is an intensive property. What will be the relation between Cp and c for 1 mol of water?
Ans.
For water, molar heat capacity = 18 × Specific heat or
Cp = 18 × c
But, specific heat,
C = 4.18 J g-1 K-1 Heat capacity,
Cp = 18 × 4.18 JK 1 = 75.24 JK-1
Q.40. The difference between CP and CV can be derived using the empirical relation H = U + pV. Calculate the difference between CP and CV for 10 moles of an ideal gas.
Ans. Given that, Cv = heat capacity at constant volume,
Cp = heat capacity at constant pressure Difference between Cp and Cv is equal to gas constant (R).
∴ Cp – Cv = nR (where, n = no. of moles)
= 10 × 8.314 = 83.14J
Q.41. If the combustion of 1g of graphite produces 20.7 kJ of heat, what will be molar enthalpy change? Give the significance of sign also.
Ans. Molar enthalpy change for graphite (ΔH)
= enthalpy change for 1 g × molar mass of C = -20.7 × 12 = -2.48 × 102 kJ mol-1
Since the sign of ΔH = -ve, it is an exothermic reaction.
Q.42. The net enthalpy change of a reaction is the amount of energy required to break all the bonds in reactant molecules minus amount of energy required to form all the bonds in the product molecules. What will be the enthalpy change for the following reaction.
H2(g) + Br2(g) → 2HBr(g)
Given that Bond energy of H2, Br2 and HBr is 435 kJ mol–1, 192 kJ mol–1 and 368 kJ mol–1 respectively.
Ans. ΔrHΘ ∑B.E.(reactants) -∑B.E.(products)
= B.E.H2 + B.E.Br2 - 2 × B.E. HBr
= 435 + 192 - (2 × 368)
= - 109 kJ mol-1
Q.43. The enthalpy of vapourisation of CCl4 is 30.5 kJ mol–1. Calculate the heat required for the vapourisation of 284 g of CCl4 at constant pressure. (Molar mass of CCl4 = 154 g mol–1).
Ans. Given that enthalpy of vaporization of 1 mole of CCI4 = 30.5 kJ/mol.
It means 1 mole of CCl4 = 154 g.
154 g requires heat of vaporization = 30.5 kJ/mol.
∴ Heat required for vapourisation of 284 g of CCl4
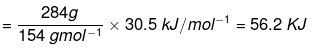
Q.44. The enthalpy of reaction for the reaction:
2H2(g) + O2(g) → 2H2O(l) is ∆rHΘ = – 572 kJ mol–1.
What will be standard enthalpy of formation of H2O(l) ?
Ans. The standard enthalpy change for the formation of one mole of a compound from its elements in their most stable states of aggregation (also known as reference states) is called Standard Molar Enthalpy of Formation. Its symbol is ∆fHΘ.
According to the definition of standard enthalpy of formation, the enthalpy change for the following reaction will be standard enthalpy of formation of H2O(l).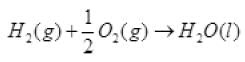
or the standard enthalpy of formation of H2O(l) will be half of the enthalpy of the given equation i.e., ∆rHΘ is also halved.
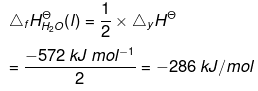
Q.45. What will be the work done on an ideal gas enclosed in a cylinder, when it is compressed by a constant external pressure, pext in a single step as shown in Figure. Explain graphically.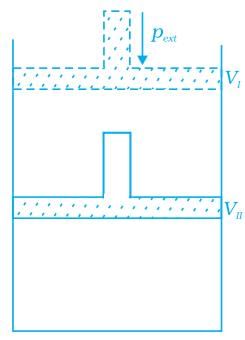 Ans. Let us consider a cylinder which contains one mole of an ideal gas fitted with a frictionless piston. Total volume of the gas is Vi and pressure of the gas inside is p. If external pressure is pext which is greater than p, piston is moved inward till the pressure inside becomes equal to pext. Let this change be achieved in a single step and the final volume be Vf. W = Pext (ΔV). Work done is equal to the shaded area ABVIVII.
Ans. Let us consider a cylinder which contains one mole of an ideal gas fitted with a frictionless piston. Total volume of the gas is Vi and pressure of the gas inside is p. If external pressure is pext which is greater than p, piston is moved inward till the pressure inside becomes equal to pext. Let this change be achieved in a single step and the final volume be Vf. W = Pext (ΔV). Work done is equal to the shaded area ABVIVII.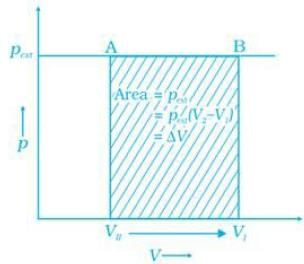
Q.46. How will you calculate work done on an ideal gas in a compression, when change in pressure is carried out in infinite steps?
Ans. A process or change is said to be reversible, if a change is brought out in such a way that the process could, at any moment, be reversed by an infinitesimal change.
Work done can be calculated from pV-plot when pressure is not constant and changes are in infinite steps (reversible conditions) during compression from initial volume, Vi to final volume, Vf. Work done on the gas is represented by the shaded area.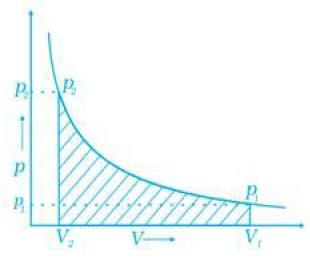
Q.47. Represent the potential energy/enthalpy change in the following processes graphically.
(a) Throwing a stone from the ground to roof
In which of the processes potential energy/enthalpy change is contributing factor to the spontaneity?
Ans. (a) On throwing stone from ground to the roof we need to supply energy to the stone. Graphically, it can be represented as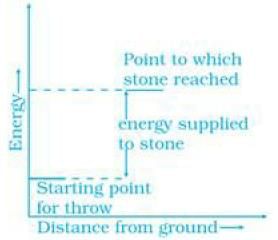 (b) In the reaction heat is evolved it means the process is followed by decrease in energy. It can be represented as
(b) In the reaction heat is evolved it means the process is followed by decrease in energy. It can be represented as
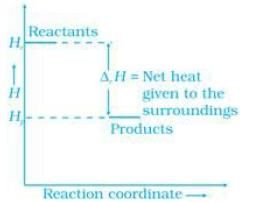
Energy increases in (a) part and decreases in (b). Hence, in process (b), the enthalpy change is the contributing factor to the spontaneity.
Q.48. Enthalpy diagram for a particular reaction is given in Figure. Is it possible to decide spontaneity of a reaction from given diagram. Explain.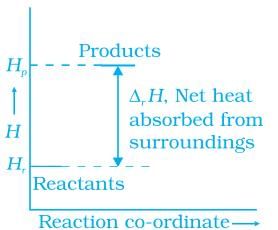 Ans. No, enthalpy is not the only criteria for spontaneity we need to consider enthalpy and entropy both.
Ans. No, enthalpy is not the only criteria for spontaneity we need to consider enthalpy and entropy both.
Q.49. 1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in Figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.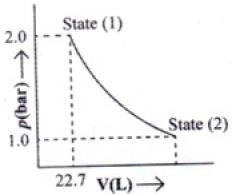 Ans. From the given diagram, it is very clear that it is a reversible change because the process is
Ans. From the given diagram, it is very clear that it is a reversible change because the process is
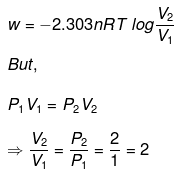
carried out in infinite no. of steps
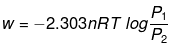
= - 2.303 x 1 mol x 8.314 J mol-1 K-1 x 298 K-1 x log 2
= - 2.303 x 8.314 x 298 x 0.3010 J = -1717.46 J
Q.50. An ideal gas is allowed to expand against a constant pressure of 2 bar from 10 L to 50 L in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work done be higher or lower than the earlier case? (Given that 1 L bar = 100 J)
Ans. Work done in the process can be calculated as
w = -Pex (Vf -Vt)= -2 × 40 = -80 bar = -8 kJ
The negative sign shows that work is done by the system on the surroundings. Work done will be more in the reversible expansion because internal pressure and external pressure are almost same at every step.
MATCHING ANSWER TYPE QUESTION
Q.51. In the following questions more than one correlation is possible between options of both columns.
Match the following :
| A | B |
| (i) Adiabatic process | (a) Heat |
| (ii) Isolated system | (b) At constant volume |
| (iii) Isothermal change | (c) First law of thermodynamics |
| (iv) Path function | (d) No exchange of energy and matter |
| (v) State function | (e) No transfer of heat |
| (vi) ∆U = q | (f) Constant temperature |
| (vii) Law of conservation of energy | (g) Internal energy |
| (viii) Reversible process | (h) pext = 0 |
| (ix) Free expansion | (i) At constant pressure |
| (x) ∆H = q | (j) Infinitely slow process which proceeds through a series of equilibrium states. |
| (xi) Intensive property | (k) Entropy |
| (xii) Extensive property | (l) Pressure |
| (m) Specific heat |
Ans. (i) → (e); (ii) → (d); (iii) → (f); (iv) → (a); (v) → (g), (k), (L); (vi) → (b); (vii) → (c); (viii) →(j); (ix) → (h); (x) → (i); (xi) → (a), (l), (m); (xii) → (g), (k)
Q.52. Match the following processes with entropy change:
| Reaction | Entropy change |
| (i) A liquid vapourises | (a) ∆S = 0 |
| (ii) Reaction is non-spontaneous at all temperatures and ∆H is positive | (b) ∆S = positive |
| (iii) Reversible expansion of an ideal gas | (c) ∆S = negative |
Ans.
| Reaction | Entropy change |
| (i) A liquid vapourises | When liquid changes into vapour, randomness of the molecules increases thus entropy increases. |
| (ii) Reaction is non-spontaneous at all temperatures and AH is positive. | When ΔH is positive, Energy factor opposes. ΔG is positive because the process is non-spontaneous so, ΔS =-ve |
| (iii) Reversible expansion of an ideal gas | The process remains in equilibrium at every stage. |
Q.53. Match the following parameters with description for spontaneity:
| ∆ (Parameters) ∆rHΘ ∆rSΘ ∆rGΘ | Description |
| (i) + – + | (a) Non-spontaneous at high temperature. |
| (ii) – – + at high T | (b) Spontaneous at all temperatures |
| (iii) – + – | (c) Non-spontaneous at all temperatures |
Ans. (i) → (c); (ii) → (a); (iii) → (b)
Solution.
| ∆ (Parameters) ∆rHΘ ∆rSΘ ∆rGΘ | Description |
| (i) + – + | (a) When enthalpy change is positive, ∆G is positive and ∆S is negative, then the process is non-spontaneous at all temperatures. |
| (ii) – – + at high T | (b) When enthalpy change is -ve and ∆G is +ve, then the process will be non-spontaneous at very high temperature. T ∆ S > ∆ H. |
| (iii) – + – | (c) When ∆ H = -ve, ∆S = +ve then ∆G = -ve and the process will be spontaneous at all temperatures. |
Q.54. Match the following :
| (i) Entropy of vapourisation | (a) decreases |
| (ii) K for spontaneous process | (b) is always positive |
| (iii) Crystalline solid state | (c) lowest entropy |
| (iv) ∆U in adiabatic expansion of ideal gas | (d) 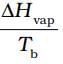 |
Ans. (i) → (b), (d); (ii) → (b); (iii) → (c); (iv) → (a)
Solution.
| Column I | Column II |
| (i) Entropy of vaporisation | ∆Hvap/Tb |
| (ii) K for spontaneous process | Since ∆rGΘ = ∆rHΘ - T ∆rSΘ = -RT |
| (iii) Crystalline solid state | Always has the lowest entropy because the molecules in solid crystal are in most ordered form. |
| (iv) ∆ U in adiabatic expansion of ideal gas | Since ∆U = q-w in case of expansion because work is done by the system and q = 0 and ∆U = -w |
ASSERTION AND REASON ANSWER TYPE QUESTION
Q.55. In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): Combustion of all organic compounds is an exothermic reaction.
Reason (R): The enthalpies of all elements in their standard state are zero.
(1) Both A and R are true and R is the correct explanation of A.
(2) Both A and R are true but R is not the correct explanation of A.
(3) A is true but R is false.
(4) A is false but R is true.
Ans. (2)
Solution.
In combustion reaction, enthalpy of the reactants is always greater than the enthalpy of the product.
Q.56. In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): Spontaneous process is an irreversible process and may be reversed by some external agency.
Reason (R): Decrease in enthalpy is a contributory factor for spontaneity.
(1) Both A and R are true and R is the correct explanation of A.
(2) Both A and R are true but R is not the correct explanation of A.
(3) A is true but R is false.
(4) A is false but R is true.
Ans. (2)
Solution.
For spontaneous process, energy factor should be favourable means ∆H = -ve and randomness should be positive.
Q.57. In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): A liquid crystallises into a solid and is accompanied by decrease in entropy.
Reason (R): In crystals, molecules organise in an ordered manner.
(1) Both A and R are true and R is the correct explanation of A.
(2) Both A and R are true but R is not the correct explanation of A.
(3) A is true but R is false.
(4) A is false but R is true.
Ans. (1)
Solution.
When a liquid crystallizes, its entropy decreases. Since in crystalline form, the molecules are more ordered.
LONG ANSWER TYPE QUESTION
Q.58. Derive the relationship between ∆H and ∆U for an ideal gas. Explain each term involved in the equation.
Ans. We know that the heat absorbed at constant volume is equal to change in the internal energy i.e., ∆U = qV. But most of chemical reactions are carried out not at constant volume, but in flasks or test tubes under constant atmospheric pressure ∆U = qp - p∆V at constant pressure, where qp is heat absorbed by the system and - p∆V represent expansion work done by the system.
Let us represent the initial state by subscript 1 and final state by 2.
We can rewrite the above equation as
U2 - U1 = p(V2 - V1)
On rearranging, we get
qp = (U2 + pV2) - (U1 + pV1) ....(1)
Now, we can define another thermodynamic function, the enthalpy H [Greek word enthalpie, to warm or heat content] as:
H = U + pV ...( 2)
So, equation (1) becomes
qp = H2 - H1 = AH
Although, q is a path dependent function, H is a state function because it depends on U, p and V, all of which are state functions. Therefore, ∆H is independent of path. Hence, qp is also independent of path.
For finite changes at constant pressure, we can write equation (2) as
∆H = ∆U + ∆pV
Since p is constant, we can write:
∆H = ∆U + p∆V ...(3)
It is important to note that when heat is absorbed by the system at constant pressure, we are actually measuring changes in the enthalpy.
Remember ∆H = qp, heat absorbed by the system at constant pressure.
∆H is negative for exothermic reactions which evolve heat during the reaction and ∆H is positive for endothermic reactions which absorb heat from the surroundings.
At constant volume (∆V = 0). ∆U = qv, therefore, equation (3) becomes
∆H = ∆U = qv
Let us consider a reaction involving gases. If VA is the total volume of the gaseous reactants, VB is the total volume of the gaseous products, nA is the number of moles of gaseous reactants and nB is the number of moles of gaseous products, all at constant pressure and temperature, then using the ideal gas law, we write,
pVA = nART
and pVB = nBRT
Thus, pVB - pVA = nBRT - nART = (nB - nA)RT
or p(VB -VA) = (nB - nA)RT
or p ∆V = ∆n gRT ... (4)
Here, ∆ng refers to the number of moles of gaseous products minus the number of moles of gaseous reactants.
Substituting the value of p∆V from equation (4) in equation (3), we get
∆H = ∆U + ∆ngRT ...(5)
Q.59. Extensive properties depend on the quantity of matter but intensive properties do not. Explain whether the following properties are extensive or intensive.
Mass, internal energy, pressure, heat capacity, molar heat capacity, density, mole fraction, specific heat, temperature and molarity.
Ans. In thermodynamics, a distinction is made between extensive properties and intensive properties. An extensive property is a property whose value depends on the quantity or size of matter present in the system. For example, the following are extensive properties: mass, volume, internal energy, enthalpy, heat capacity.
Those properties which do not depend on the quantity or size of matter present, are known as intensive properties.
For example, the following are intensive properties: temperature, density, pressure. A molar property, χm, is the value of an extensive property χ of the system for 1 mol of the substance. If n is the amount of matter, χm = χ/n , is independent of the amount of matter. The ratio of two extensive properties is always an intensive property.
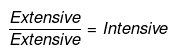
Example: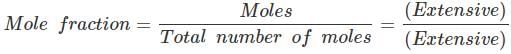
Q.60. Graphically show the total work done in an expansion when the state of an ideal gas is changed reversibly and isothermally from (pi , Vi) to (pf , Vf). With the help of a pV plot compare the work done in the above case with that carried out against a constant external pressure pf.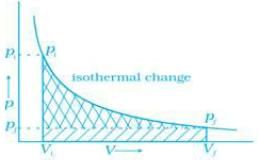 Ans. (i) Reversible work is represented by the combined areas
Ans. (i) Reversible work is represented by the combined areas and
and .
.
(ii) Work against constant pressure, pf is represented by the area  Work (i) > Work (ii).
Work (i) > Work (ii).





















