NCERT Exemplars: Atoms | Physics Class 12 - NEET PDF Download
MULTIPLE CHOICE QUESTIONS
Q.1. Taking the Bohr radius as a0 = 53 pm, the radius of Li++ ion in its ground state, on the basis of Bohr’s model, will be about
(a) 53 pm
(b) 27 pm
(c) 18 pm
(d) 13 pm
Ans. (c)
Solution.
Bohr's radius of orbit (for Hydrogen and H2-like atoms):
For an electron around a stationary nucleus, the electrostatics force of attraction provides the necessary centripetal force.
i.e., (1/4πε0)((Ze)e/r2) = mv2/r ...(i)
Also mvr = nh/2π ...(ii)
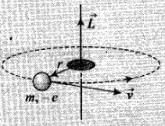
From equation (i) and (ii), radius of nth orbit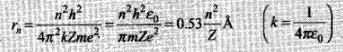
⇒ rn ∝ n2/Z or rn ∝ 1/Z
rn = a0(n2/Z), where a0 = the Bohr radius = 53 pm
The atomic number (Z) of lithium is 3.
As 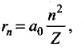
Therefore, the radius of Li++ ion in its ground state, on the basis of Bohr’s model, will be about 1/3 times to that of Bohr radius.
Therefore, the radius of lithium ion is near r = 53/3 ≈ 18pm.
Q.2. The binding energy of a H-atom, considering an electron moving around a fixed nuclei (proton), 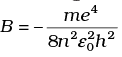 (m = electron mass).
(m = electron mass).
If one decides to work in a frame of reference where the electron is at rest, the proton would be moving arround it. By similar arguments, the binding energy would be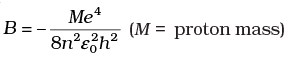
This last expression is not correct because
(a) n would not be integral.
(b) Bohr - quantisation applies only to electron
(c) The frame in which the electron is at rest is not inertial.
(d) The motion of the proton would not be in circular orbits, even approximately.
Ans. (c)
Solution.
As the mass of an electron is negligible as compared to proton. So the centripetal force cannot provide the electrostatic force, 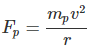 . So the given expression is not true, as it form non-inertial frame of reference due to me<<<mp or centripetal force on Fe <<< Fp. So verifies answer (c).
. So the given expression is not true, as it form non-inertial frame of reference due to me<<<mp or centripetal force on Fe <<< Fp. So verifies answer (c).
Q.3. The simple Bohr model cannot be directly applied to calculate the energy levels of an atom with many electrons. This is because
(a) Of the electrons not being subject to a central force
(b) Of the electrons colliding with each other
(c) Of screening effects
(d) The force between the nucleus and an electron will no longer be given by Coulomb’s law
Ans. (a)
Solution.
The simple Bohr model cannot be directly applied to calculate the energy levels of an atom with many electrons because when we derive the formula for radius/energy levels etc, we make the assumption that centripetal force is provided only by electrostatic force of attraction by the nucleus. Hence, this will only work for single electron atoms. In multi-electron atoms, there will also be repulsion due to other electrons. The simple Bohr model cannot be directly applied to calculate the energy levels of an atom with many electrons.
Q.4. For the ground state, the electron in the H-atom has an angular momentum = ћ, according to the simple Bohr model. Angular momentum is a vector and hence there will be infinitely many orbits with the vector pointing in all possible directions. In actuality, this is not true,
(a) Because Bohr model gives incorrect values of angular momentum
(b) Because only one of these would have a minimum energy
(c) Angular momentum must be in the direction of spin of electron
(d) Because electrons go around only in horizontal orbits
Ans. (a)
Solution.
According to Bohr’s second postulate of atomic model, angular momentum of revolving electron must be some integral multiple of h/2π. so the Bohr’s model does not give correct value of angular momentum. Hence verified answer (a).
Q.5. O2 molecule consists of two oxygen atoms. In the molecule, nuclear force between the nuclei of the two atoms
(a) is not important because nuclear forces are short-ranged.
(b) is as important as electrostatic force for binding the two atoms.
(c) cancels the repulsive electrostatic force between the nuclei.
(d) is not important because oxygen nucleus have equal number of neutrons and protons
Ans. (a)
Solution.
Nuclear forces is too much stronger. Only attractive force as compared to electrostatic repulsive force and nuclear force decreases to zero on increasing distance. So in case of oxygen molecule, the distance between atoms of oxygen is larger as compared to the distances between nucleons in a nucleus. So force between the nuclei of two oxygen atoms is not important as nuclear forces are short ranged forces. Hence verified answer (d).
Q.6. Two H atoms in the ground state collide inelastically. The maximum amount by which their combined kinetic energy is reduced is
(a) 10.20 eV
(b) 20.40 eV
(c) 13.6 eV
(d) 27.2 eV
Ans. (a)
Solution.
Total energy of two H-atom in ground state
=2(-13.6)=-27.2 eV
The maximum amount by which their combined kinetic energy is reduced when any one H-atom goes into first excited state after the inelastic collision i.e., the total energy of two H-atom after inelastic collision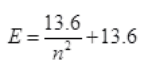
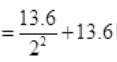 [ for excited state (n=2)]
[ for excited state (n=2)]
=3.4+13.6=17.0 eV
So loss in KE due to inelastic collision
=27.2-17.0=10.2 eV
Q.7. A set of atoms in an excited state decays.
(a) in general to any of the states with lower energy
(b) into a lower state only when excited by an external electric field
(c) all together simultaneously into a lower state
(d) to emit photons only when they collide
Ans. (a)
Solution. A set of atoms in an excited state decays in general to any of the states with lower energy.
Q.8. An ionised H-molecule consists of an electron and two protons.
The protons are separated by a small distance of the order of angstrom. In the ground state,
(a) The electron would not move in circular orbits
(b) The energy would be (2)4 times that of a H-atom
(c) The electrons, orbit would go around the protons
(d) The molecule will soon decay in a proton and a H-atom
Ans. (a, c)
Solution.
In H-molecule two nucleus of 2 H-atoms are separated of the order of angstrom, i.e. of order of nuclear forces. One electron will revolve around the protons. Hence verifies answer (a) and (c).
Q.9. Consider aiming a beam of free electrons towards free protons. When they scatter, an electron and a proton cannot combine to produce a H-atom,
(a) Because of energy conservation.
(b) Without simultaneously releasing energy in the from of radiation.
(c) Because of momentum conservation.
(d) Because of angular momentum conservation.
Ans. (a, b)
Solution.
The binding energy of H-atom is larger as compared to the energy of free electron. Large amount of energy is required so that electron can reach near the proton which is possible when nuclear force (attractive) acts between e and p become of order of nuclear force, it is not possible without energy conservation (a) and (b).
Q.10. The Bohr model for the spectra of a H-atom
(a) Will not be applicable to hydrogen in the molecular from
(b) Will not be applicable as it is for a He-atom
(c) Is valid only at room temperature
(d) Predicts continuous as well as discrete spectral lines
Ans. (a, b)
Solution.
Bohr proposed a-model for hydrogen atom which is also applicable for some lighter atoms in which a single electron revolves around a stationary nucleus of positive charge Ze (called hydrogen like atom, e.g.: H, He+, Li+2, Na+1 etc). It is not applicable to hydrogen in the molecular form and also, it will not be applicable as it is for a He-atom.
Q.11. The Balmer series for the H-atom can be observed
(a) If we measure the frequencies of light emitted when an excited atom falls to the ground state
(b) If we measure the frequencies of light emitted due to transitions between excited states and the first excited state
(c) In any transition in a H-atom
(d) As a sequence of frequencies with the higher frequencies getting closely packed
Ans. (b, d)
Solution.
When electron jumps from higher energy level to first energy level, the spectrum of light is called Balmer series. Spectrum lines become closer if electron jumps from higher energy level to ground level. Hence verifies answers (b) and (d).
Q.12. Let 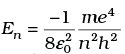 be the energy of the nth level of H-atom. If all the H-atoms are in the ground state and radiation of frequency (E2 - E1)/h falls on it,
be the energy of the nth level of H-atom. If all the H-atoms are in the ground state and radiation of frequency (E2 - E1)/h falls on it,
(a) It will not be absorbed at all
(b) Some of atoms will move to the first excited state
(c) All atoms will be excited to the n = 2 state
(d) No atoms will make a transition to the n = 3 state
Ans. (b,d)
Solution.
Let E2 and E1 be the energy corresponding to n = 2 and n = 1 respectively. If radiation of energy ∆E = (E2 – E1) = hf incident on a sample where all the H-atoms are in the ground state, according to Bohr model some of the atoms will move to the first excited state. As this energy is not sufficient for transition from n = 1 to n =3, hence no atoms will make a transition to the n = 3 state.
Q.13. The simple Bohr modle is not applicable to He4 atom because
(a) He4 is an inert gas.
(b) He4 has neutrons in the nucleus.
(c) He4 has one more electron.
(d) Electrons are not subject to central forces
Ans. (c, d)
Solution.
Bohr’s atomic model is applicable only for one electron and in He4 there are two electrons. Electrons are not subject to central forces due to longer distance than nuclear size verifies answer (c) and (d).
VERY SHORT ANSWER TYPE QUESTIONS
Q.14. The mass of a H-atom is less than the sum of the masses of a proton and electron. Why is this?
Ans. During formation of an atom with neucleon and electrons, it need the energy to bind the nucleons together in nucleus. This energy comes from Einstein mass- energy relation
E=ΔmC2
Where Δm=[Zmp+(A-Z)mn]-M
So the mass of a H atom is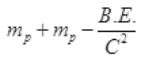
Where B.E. = 13.6 eV
Q.15. Imagine removing one electron from He4 and He3. Their energy levels, as worked out on the basis of Bohr model will be very close. Explain why.
Ans. Bohr model is applicable for hydrogen atom-and some lighter atoms in which a single electron revolves around a stationary nucleus of positive charge Ze (called hydrogen like atom). If we remove one electron from He4 and He3, atoms contain one electron and becomes hydrogen like atoms. Now we can apply Bohr model to define the energy levels.
Q.16. When an electron falls from a higher energy to a lower energy level, the difference in the energies appears in the form of electromagnetic radiation. Why cannot it be emitted as other forms of energy?
Ans. The electrons are charged particles. When an electron falls from a higher energy to a lower energy level, it accelerates. We know accelerating charged particle radiates energy in the form of electromagnetic radiation.
Q.17. Would the Bohr formula for the H-atom remain unchanged if proton had a charge (+4/3)e and electron a charge (−3/4)e, where e = 1.6 × 10–19C. Give reasons for your answer.
Ans. According to Bohr, for an electron around a stationary nucleus the electrostatics force of attraction provides the necessary centripetal force.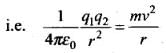 ..(i)
..(i)
Hence the magnitude of electrostatic force F ∞ q1 x q2
If proton had a charge (+4/3)e and electron a charge (-3/4)e, then the Bohr formula for the H-atom remains same, since the Bohr formula involves only the product of the charges which remain constant for given values of charges.
Q.18. Consider two different hydrogen atoms. The electron in each atom is in an excited state. Is it possible for the electrons to have different energies but the same orbital angular momentum according to the Bohr model?
Ans. Bohr postulated that an electron in an atom can move around the nucleus in a certain circular stable orbits without emitting radiations.
Bohr found that the magnitude of the electron’s angular momentum is
quantized i.e 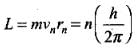
where n = 1 , 2, 3...... each value o f n corresponds to a permitted value o f the orbit radius.
rn = Radius of nth orbit, vn = corresponding speed
Thus, the angular momentum (L) of the orbiting electron is quantised
According to Bohr model electrons having different energies belong to different levels haying different values o f n. So, their angular momenta will be different, as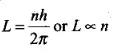
SHORT ANSWER TYPE QUESTIONS
Q.19. Positronium is just like a H-atom with the proton replaced by the positively charged anti-particle of the electron (called the positron which is as massive as the electron). What would be the ground state energy of positronium?
Ans. As in the new H-atom (positronium) proton is replaced by positron of mass m=me/2 as under
Mass of positronium=m = 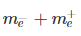
m=me+me=2me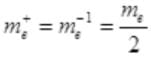
As En=-13.6 and so energy of positron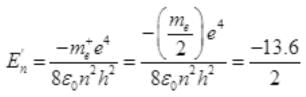

E'n = -6.8eV
Q.20. Assume that there is no repulsive force between the electrons in an atom but the force between positive and negative charges is given by Coulomb’s law as usual. Under such circumstances, calculate the ground state energy of a He-atom.
Ans. For H atom Z=1 and n=1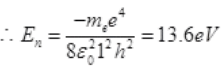
For He-atom, Z=4 and n=1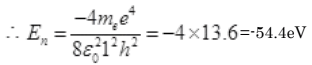
Q.21. Using Bohr model, calculate the electric current created by the electron when the H-atom is in the ground state.
Ans. Let for an electron of H atom velocity in orbit=v m/s
Radius of orbit=a0 = Bohr’s radius
So the number of revolutions per second 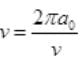
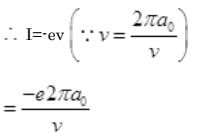
(-) sign shows that the direction of current is opposite to the direction of motion of electron.
Q.22. Show that the first few frequencies of light that is emitted when electrons fall to the nth level from levels higher than n, are approximate harmonics (i.e. in the ratio 1 : 2: 3...) when n >>1.
Ans.
Frequency of emitted radiation:
Wave number/wavelength:
Wave number is the number of waves in unit length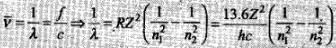
Number of spectral lines: If an electron jumps from higher energy orbit to lower energy orbit to lower energy orbit it emits radiations with various spectral lines.
If electron falls from orbit n2 to n1 then the number of spectral lines emitted is given by
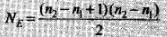
If electron falls from nth orbit to ground state (i.e. n2 = n and n1 = 1), then number of spectral lines emitted NE = n(n-1)/2
The frequency of any line in a series in the spectrum of hydrogen like atoms corresponding to the transition of electrons from (n + p) level to nth level can be expressed as a difference of two terms;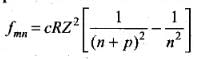
where, m = n + p, (p = 1, 2 , 3 , ...) and R is Rydberg constant.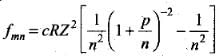
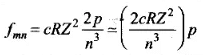
[By Binomial theorem (1 + x )n - 1 + nx if |x| < 1]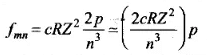
Hence, the first few frequencies of light that is emitted when electrons fall to the nth level from levels higher than n, are approximately harmonic (i.e., in the ratio 1 : 2 : 3 ...) when n » 1.
Q.23. What is the minimum energy that must be given to a H atom in ground state so that it can emit an Hγ line in Balmer series. If the angular momentum of the system is conserved, what would be the angular momentum of such Hγ photon?
Ans. Balmer series: Named after Johann Balmer, who discovered the Balmer formula, an empirical equation to predict the Balmer series, in 1885. Balmer lines are historically referred to as "H-alpha". corresponds to transition 3 → 2, "H-beta"
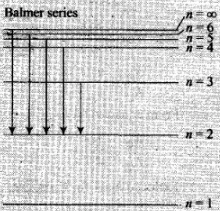
corresponds to transition 4 → 2, "H-gamma"
corresponds to transition 5 → 2 and so on.
where H is the element hydrogen. Four of the Balmer lines are in the technically "visible" part of the spectrum, with wavelengths longer than 400 nm and shorter than 700 nm. Parts of the Balmer series can be seen in the solar spectrum. H-alpha is an important line used in astronomy to detect the presence of hydrogen.
From above discussion it is clear that HY in Balmer series corresponds to transition n = 5 to n = 2. Initially the electron in ground state i.e., from n = 1 must first should be placed in state n = 5.
From above discussion it is clear that Hγ in Balmer series corresponds to transition n = 5 to n = 2. Initially the electron in ground state i.e., from n = 1 must first should be placed in state n = 5.
Energy required for the transition from n = 1 to n - 5 is given by
E = E5 - E1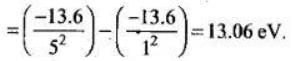
As angular momentum should be conserved, hence angular momentum corresponding to Hγ photon = change in angular momentum of electron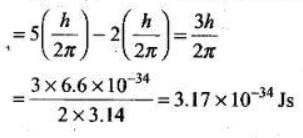
LONG ANSWER TYPE QUESTIONS
Q.24. The first four spectral lines in the L yman serics of a H-atom are λ = 1218 Å, 1028 Å, 974.3 Å and 951.4 Å. If instead of Hydrogen, we consider Deuterium, calculate the shift in the wavelength of these lines.
Ans. Reduced mass of H atom (mass defect) μH then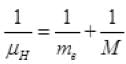 (M is mass of H atom)
(M is mass of H atom)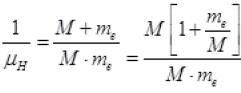 ( ∵ M>>>me)
( ∵ M>>>me)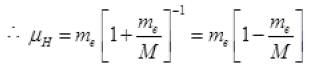
For Deuterium M = 2M
Reduced mass of Deuterium = μD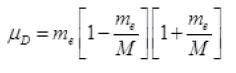
Total energy En of the electron revolving in an nth stationary orbit,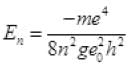
m is the reduced mass of the electron and proton in H atom.
So hv = Eni - Enf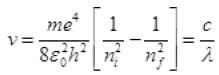
v ∝ m (reduced mass)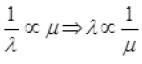
For hydrogen and deuterium 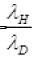
So, 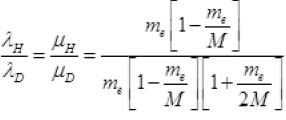
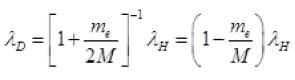
λD = λH(0.99973)
λH = Å, Å, Å and Å (Given)
λD1 = Å = 1214 Å
λD2 = 0.9973 x 1028 = 1025Å
λD3 = 0.9973 x 974 = Å
λD4 = 0.9973 x 954 = Å
Q.25. Deutrium was discovered in 1932 by Harold Urey by measuring the small change in wavelength for a particular transition in 1H and 2H. This is because, the wavelength of transition depend to a certain extent on the nuclear mass. If nuclear motion is taken into account then the electrons and nucleus revolve around their common centre of mass. Such a system is equivalent to a single particle with a reduced mass µ, revolving around the nucleus at a distance equal to the electron-nucleus separation. Here µ = meM /(me +M) where M is the nuclear mass and me is the electronic mass. Estimate the percentage difference in wavelength for the 1st line of the Lyman series in 1H and 2H. (Mass of 1H nucleus is 1.6725 × 10–27 kg, Mass of 2H nucleus is 3.3374 × 10–27 kg, Mass of electron = 9.109 × 10–31 kg.)
Ans. Total energy of electron in nth stable orbit in H or like atom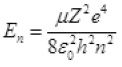
μ = reduced mass of electron, proton and neutron (mass defect)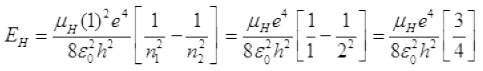
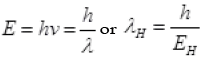
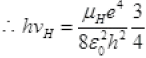
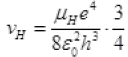
The percentage difference in the wavelength = 
Percent change in wavelength
% change 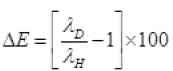
∵ ΔE = (E1 - E2) …(I)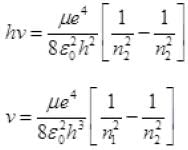
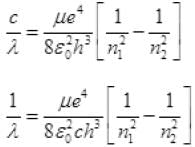
as μ = mass defect, e,ε, 0 c, and h are constants for an atom.
∴ λ ∝ 1/h
So eqn. Ist can be written as percentage change in the wavelength = 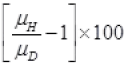
∵ 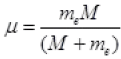 (Given)
(Given)
∴ Percentage change in wavelength = 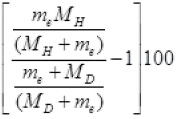
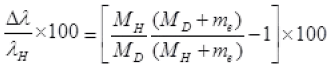
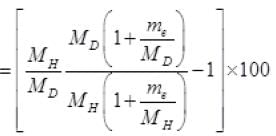
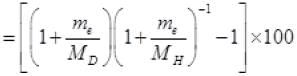
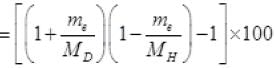
Me << MD so neglecting the higher degree term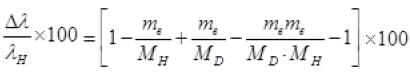
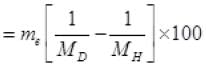
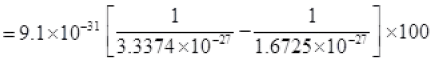
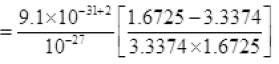
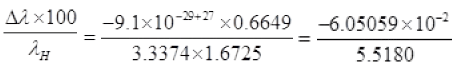
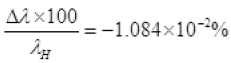 Decrease in wavelength.
Decrease in wavelength.
(-) sign shows that λD < λH.
Q.26. If a proton had a radius R and the charge was uniformly distributed, calculate using Bohr theory, the ground state energy of a H-atom when (i) R = 0.1 Å, and (ii) R = 10 Å.
Ans. (i) Consider in H atom nucleus as point charge electron is revolving around nucleus with speed v and radius rA. The Colombian force provides centripetal force to revolve around nucleus.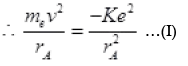
Here K = 1/4πε0
(-) sign shows the force of attraction.
By Bohr’s postulate, angular momentum= nh/2π
mvrA = nh/2π
v = nh/2πmrA [From I]
[From I]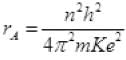 ...(II)
...(II)
For ground state n = 1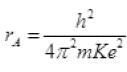
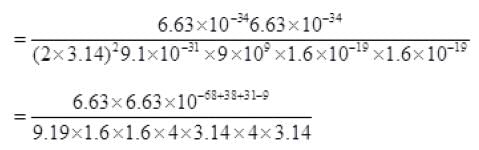
= rA=0.53 Å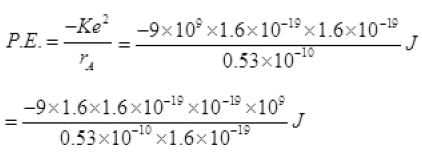

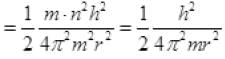 (n = 1 for ground state)
(n = 1 for ground state)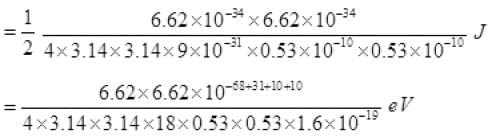
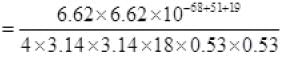
K.E. = 0.1373 × 102 eV = 13.7 eV
P.E. = 27.2 eV
(ii) Now for spherical nucleus of radius, R, electron moves charge inside the nucleus R>>rb then electron moves inside the nucleus. Then (rb is radius of new Bohr’s orbit of revolving electron)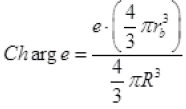
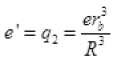
q1 = e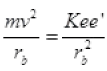 (By Coulomb’s law)
(By Coulomb’s law)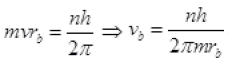 (By Bohr’s postulate)
(By Bohr’s postulate)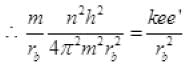
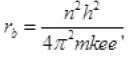
Now for ground state of H, n=1 and  then
then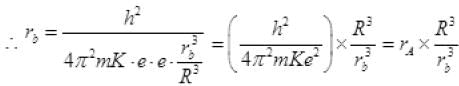
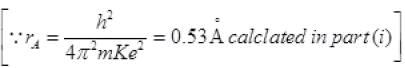
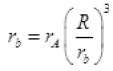
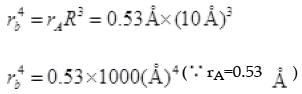
rb= [530A4]1/4 Å < R Å
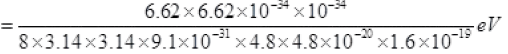
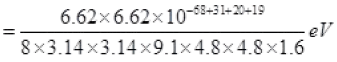
 = 0.001656 × 102 eV
= 0.001656 × 102 eV
K.E = 0.167eV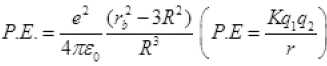

From part (i)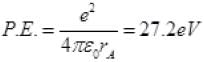
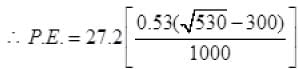
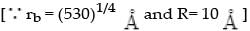
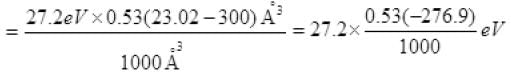
P.E. = 3992.9/1000 = -3.99eV
K.E. = 0.167 eV
Q.27. In the Auger process an atom makes a transition to a lower state without emitting a photon. The excess energy is transferred to an outer electron which may be ejected by the atom. (This is called an Auger electron). Assuming the nucleus to be massive, calculate the kinetic energy of an n = 4 Auger electron emitted by Chromium by absorbing the energy from a n = 2 to n = 1 transition.
Ans. The energy En of the nth state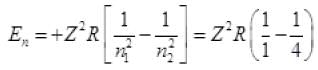 (for n1 = 1, n2 = 2)
(for n1 = 1, n2 = 2)
Z = 24
R = Rydberg constt.
∴ En = 3/4 Z2R
The energy required to eject an electron from n = 4 state is
E4 = Z2R 1/42 = 1/16 Z2R
Energy given to electron is converted into K.E. of ejected electron.
Hence, the K.E. of Auger (ejected) electron= En - E4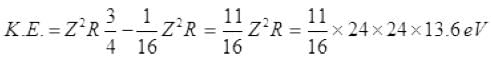
K.E. = 11 × 36 × 13.6 = 5385.6 eV
Q.28. The inverse square law in electrostatics is 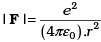 for the force between an electron and a proton. The (1/r) dependence of |F| can be understood in quantum theory as being due to the fact that the ‘particle’ of light (photon) is massless. If photons had a mass mp, force would be modified to
for the force between an electron and a proton. The (1/r) dependence of |F| can be understood in quantum theory as being due to the fact that the ‘particle’ of light (photon) is massless. If photons had a mass mp, force would be modified to 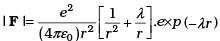 where
where 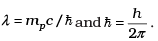 Estimate the change in the ground state energy of a H-atom if mp were 10-6 times the mass of an electron.
Estimate the change in the ground state energy of a H-atom if mp were 10-6 times the mass of an electron.
Ans. Mass of photon =9.1 × 10-31 × 10-6 kg
= 9.1 × 10-37 kg
Wavelength associated with a photon = h/mpc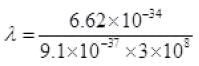
 =2.4×10-7>>rA
=2.4×10-7>>rA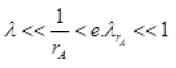
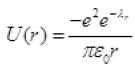
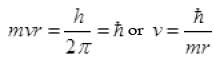 ...(I)
...(I)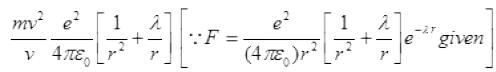
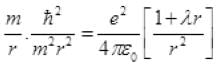
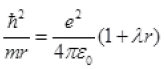
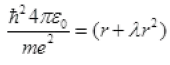
If λ=0, 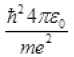 [neglecting r2]
[neglecting r2]
∵ λA>>rB and δ
Taking rA+r+λr2[∵ δ]
rA= (rA δ)+λ(rA δ) (put δ2)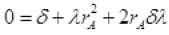 (neglecting small term δ2)
(neglecting small term δ2)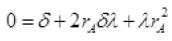
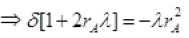
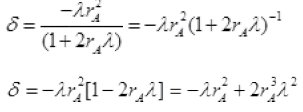
∴ λ and rA << 1 so 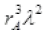 is very small so by neglecting it we get,
is very small so by neglecting it we get,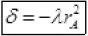
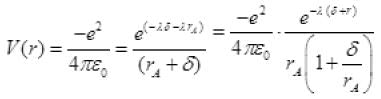
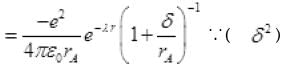
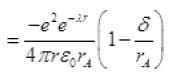
V(r) = -27.2 eV remains unchanged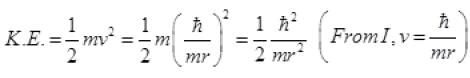
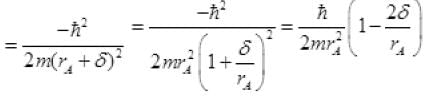
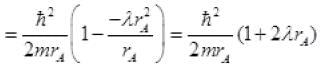
= 13.6 eV (1 + 2λrA)
Total energy = 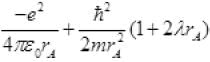
=[-27.2+13.6(1+2λrA)]eV
=-27.2+13.6+27.2λrA eV
Total E= -13.6+27.2 λrA
Change in energy =-13.6+27.2λrA-(-13.6)=27.2λrA eV
Q.29. The Bohr model for the H-atom relies on the Coulomb’s law of electrostatics. Coulomb’s law has not directly been verified for very short distances of the order of angstroms. Supposing Coulomb’s law between two opposite charge + q1, –q2 is modified to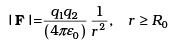
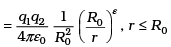
Calculate in such a case, the ground state energy of a H-atom, if ε = 0.1, R0 = 1Å.
Ans. Case I: when r ≤ R0 = 1 Å
Let ε = 2 + δ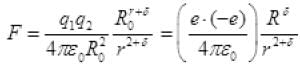 [q1=e, q2=-e]
[q1=e, q2=-e] [(-) ve sign shows force of attraction]
[(-) ve sign shows force of attraction]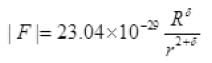
The electrostatic force of attraction between positively charged nucleus and negatively charged electron provides necessary centripetal force.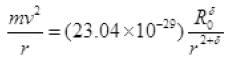
Let 23.04 × 10-29= 

By Bohr’s IInd postulate, angular momentum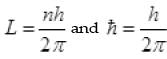 [Given in last Q.]
[Given in last Q.]
∴ L = nh
mvr = nh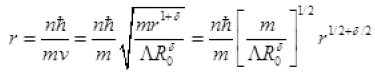
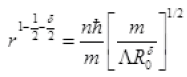
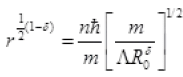
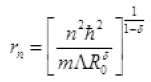
= 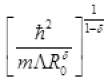 (n = 1 for ground state)
(n = 1 for ground state)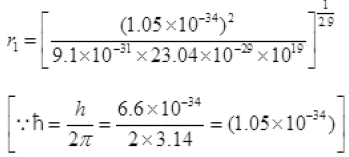
Where h = 1.05 × 10-34 JS-1
R0 = 1019 and 1 - δ = 2.9
R1 = 8 × 10-11 m= 0.08 nm
This is a radius of orbit of electron in ground state of hydrogen atom.
Velocity of electron in ground state
By IInd postulate of Bohr’s Atomic model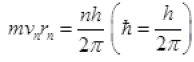
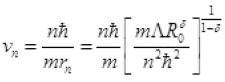
Case II: n=1, 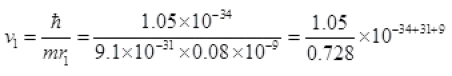
= 1.44 x 10-34+40 = 1.44 x 106 m/s
v1 = 1.44 x 106 m/s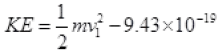
= 1/2 x 9.1 x 10-31 x (1.44 x 106)2 - 9.43 x 10-19J
= 5.9 eV
P.E. from R0 to 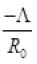
P.E from R0 to 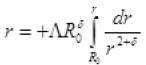
This is the P.E. of electron in ground state R0 to r = 
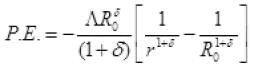
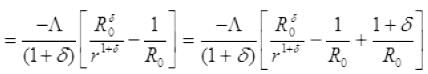
Put δ = -1.9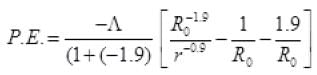
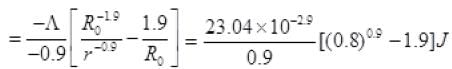
= -17.3 eV
Total E = P.E. + K.E.
=(-17.3 + 5.9) eV
Total energy = -11.4eV
This is the required total energy of electron in ground state of H-atom.
|
74 videos|314 docs|88 tests
|
FAQs on NCERT Exemplars: Atoms - Physics Class 12 - NEET
| 1. What are atoms? |  |
| 2. How are atoms formed? |  |
| 3. What are the different parts of an atom? |  |
| 4. What is the atomic number of an atom? |  |
| 5. How are atoms represented in chemical equations? |  |





















