NCERT Exemplars: Current Electricity | Physics Class 12 - NEET PDF Download
MULTIPLE CHOICE QUESTIONS - I
Q.1. Consider a current carrying wire (current I) in the shape of a circle. Note that as the current progresses along the wire, the direction of j (current density) changes in an exact manner, while the current I remain unaffected. The agent that is essentially responsible for is
(a) Source of emf.
(b) Electric field produced by charges accumulated on the surface of wire.
(c) The charges just behind a given segment of wire which push them just the right way by repulsion.
(d) The charges ahead.
Ans. (b)
Solution.
Current density (J) depends on conductivity 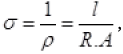 Electric field (J = σE), current and length and area of cross-section. In our options only E i.e., electric field can be varied by the charges accumulated on the surface of wire.
Electric field (J = σE), current and length and area of cross-section. In our options only E i.e., electric field can be varied by the charges accumulated on the surface of wire.
Q.2 Two batteries of emf ε1 and ε2 (ε2 > ε1) and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig 3.1.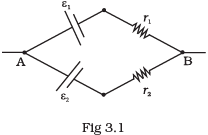 (a) The equivalent emf εeq of the two cells is between ε1 and ε2, i.e. ε1<εeq<ε2.
(a) The equivalent emf εeq of the two cells is between ε1 and ε2, i.e. ε1<εeq<ε2.
(b) The equivalent emf εeq is smaller than ε1 .
(c) The εeq is given by εeq = ε1 + ε2 always.
(d) εeq is independent of internal resistances r1 and r2.
Ans. (a)
Solution.
We know that equivalent emf εeq in parallel combination of cells is: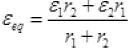
Clearly, part ‘c’ and ‘d’ are discarded by formula. This formula suggests that ε1 < εeq < ε2 . So verifies answer (a).
Q.3. A resistance R is to be measured using a meter bridge. Student chooses the standard resistance S to be 100Ω. He finds the null point at l1 = 2.9 cm. He is told to attempt to improve the accuracy.
Which of the following is a useful way?
(a) He should measure l1 more accurately.
(b) He should change S to 1000Ω and repeat the experiment.
(c) He should change S to 3Ω and repeat the experiment.
(d) He should give up hope of a more accurate measurement with a meter bridge.
Ans. (c)
Solution.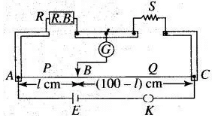 Key concept: In this problem, the concept of balanced Wheatstone bridge is to be used.
Key concept: In this problem, the concept of balanced Wheatstone bridge is to be used.
Condition of balanced wheatstone bridge: The bridge is said to be balanced if the ratio of the resistances in same branch is equal R/S =l1/(100-l1)
Wheatstone bridge is an arrangement of four resistances which can be used to measure one unknown resistance of them in terms of rest.
The percentage error in R can be minimised by adjusting the balance point near the middle of the bridge, i.e., when /, is close to 50 cm. This requires a suitable choice of S.
Since , R/S =l1/(100-l1)
Since here, R : S = 2.9 : 97.1
then the value of S is nearly 33 times to that of R. In order to make this ratio 1:1, it is necessary to reduce the value of S nearly 1/33 times, i.e., nearly 3 Ω.
Q.4. Two cells of emf’s approximately 5V and 10V are to be accurately compared using a potentiometer of length 400cm.
(a) The battery that runs the potentiometer should have voltage of 8V.
(b) The battery of potentiometer can have a voltage of 15V and R adjusted so that the potential drop across the wire slightly exceeds 10V.
(c) The first portion of 50 cm of wire itself should have a potential drop of 10V.
(d) Potentiometer is usually used for comparing resistances and not voltages.
Ans. (b)
Solution.
Key concept: The potential drop along the wires of potentiometer should be greater than emfs of cells.
In a potentiometer experiment, the emf of a cell can be measured if the potential drop along the potentiometer wire is more than the emf of the cell to be determined. Here,
values of emfs of two cells are given as 5 V and 10 V, therefore, the potential drop along
the potentiometer wire must be more than 10 V.
Q.5. A metal rod of length 10 cm and a rectangular cross-section of 1 cm x 1/2 cm is connected to a battery across opposite faces. The resistance will be
(a) Maximum when the battery is connected across 1 cm x 1/2 cm faces.
(b) Maximum when the battery is connected across 10 cm x 1 cm faces.
(c) Maximum when the battery is connected across 10 cm x 1/2 cm faces.
(d) Same irrespective of the three faces.
Ans. (a)
Solution.
As we know 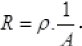 The maximum resistance will be when the value of 1/A is maximum, i.e., ‘A’ must be minimum, it is minimum when area of cross section is 1 cm x 1/2 cm. Verifies option (a).
The maximum resistance will be when the value of 1/A is maximum, i.e., ‘A’ must be minimum, it is minimum when area of cross section is 1 cm x 1/2 cm. Verifies option (a).
Q.6. Which of the following characteristics of electrons determines the current in a conductor?
(a) Drift velocity alone.
(b) Thermal velocity alone.
(c) Both drift velocity and thermal velocity.
(d) Neither drift nor thermal velocity.
Ans. (a)
Solution.
As I Anevd, So current I α vd i.e., verifies answer (a).
Although I also depends on n, the number of free electrons which increases on increasing temperature which makes more collision between electrons increases resistance or decrease current. So ans. ‘a’ verified.
MULTIPLE CHOICE QUESTIONS - II
Q.7. Kirchhoff’s junction rule is a reflection of
(a) Conservation of current density vector.
(b) Conservation of charge.
(c) The fact that the momentum with which a charged particle approaches a junction is unchanged (as a vector) as the charged particle leaves the junction.
(d) The fact that there is no accumulation of charges at a junction.
Ans. (b, d)
Solution.
Key concept: Junction rule: At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction.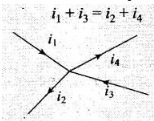 Or
Or
Algebraic sum of the currents flowing towards any point in an electric network is zero, i.e., charges are conserved in an electric network.
The proof of this rule follows from the fact that when currents are steady, there is no accumulation of charges at any junction or at any point in a line. Thus, the total current flowing in, (which is the rate at which charge flows into the junction), must equal the total current flowing out.
Kirchhoffs junction rule is also known as Kirchhoff’s current law.
So, Kirchhoffs junction rule is the reflection of conservation of charge
Important point: Sign convention of current from a junction: We are taking outgoing current from a junction as negative. And we are taking incoming current towards a junction as positive.
Q.8. Consider a simple circuit shown in Fig 3.2. stands for a variable resistance R ′. R ′ can vary from R0 to infinity. r is internal resistance of the battery (r<<R<<R0).
stands for a variable resistance R ′. R ′ can vary from R0 to infinity. r is internal resistance of the battery (r<<R<<R0).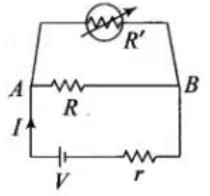 (a) Potential drop across AB is nearly constant as R ′ is varied.
(a) Potential drop across AB is nearly constant as R ′ is varied.
(b) Current through R′ is nearly a constant as R ′ is varied.
(c) Current I depends sensitively on R ′.
(d) 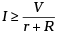 always.
always.
Ans. (a,d)
Solution.
As r << R << R0< R’ from question, R’> R and R’ and R are in parallel combination, so the equivalent resistance will be always less than R. So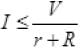 and potential across AB will remain nearly constant. It verifies answers (a) and (d).
and potential across AB will remain nearly constant. It verifies answers (a) and (d).
Q.9. Temperature dependence of resistivity ρ(T) of semiconductors, insulators and metals is significantly based on the following factors:
(a) Number of charge carriers can change with temperature T.
(b) Time interval between two successive collisions can depend on T.
(c) Length of material can be a function of T.
(d) Mass of carriers is a function of T.
Ans. (a) and (b)
Solution.
We know that resistivity (ρ) depends on mass of charge-carrier (m), relaxation time (τ). Length and mass cannot be function of T as the mass of a body is constant everywhere. So discards answer (d) and length of body changes negligibly with temperature discards answer (c).
As τ decreases on increasing T due to rise in speed of change-carriers and n increases on increasing temperature. So will affect the ρ or ρ is function of T verifies answers (a) and (b)
Q.10. The measurement of an unknown resistance R is to be carried out using Wheat stones bridge (see Fig. 3.25 of NCERT Book). Two students perform an experiment in two ways. The first students takes R2 = 1OQ and R1 = 5Ω The other student takes R2 = 1000Ω and R1 = 500Ω. In the standard arm, both take R3 = 5Ω.
Both find 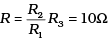 within errors.
within errors.
(a) The errors of measurement of the two students are the same.
(b) Errors of measurement do depend on the accuracy with which R2 and R1 can be measured.
(c) If the student uses large values of R2 and R1 the currents through the arms will be feeble. This will make determination of null point accurately more difficult.
(d) Wheatstone bridge is a very accurate instrument and has no errors of measurement.
Ans. (b) and (c)
Solution.
As the ratio of R2/R3 and standard resistance are same, so value of unknown resistance for both students are 10 Ω. So we can say the Wheatstone Bridge is most sensitive. The results of both students depend on the accuracy of resistances used. So answer (b) is verified.
When R1 and R2 is larger, the current through galvanometer becomes weak. It will make difficult to find out null point more accurately. So answer (c) is verified.
Q.11. In a meter bridge the point D is a neutral point (Fig 3.3).
(a) The meter bridge can have no other neutral point for this set of resistances.
(b) When the jockey contacts a point on meter wire left of D, current flows to B from the wire.
(c) When the jockey contacts a point on the meter wire to the right of D, current flows from B to the wire through galvanometer.
(d) When R is increased, the neutral point shifts to left.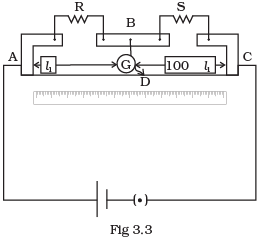 Ans. (a, c)
Ans. (a, c)
Solution.
Key concept: Meter bridge: In case of meter bridge, the resistance wire AC is 100 cm long. Varying the position of tapping point B, bridge is balanced. If in balanced position of bridge AB = l, BC = (100 – l) so that Q/P= (100-l)/l. Also P/Q=R/S=>S=(100-l)/l R When there is no deflection in galvanometer there is no current across the galvanometer, then points B and D are at same potential. That point at which galvanometer shows no deflection is called null point, then potential at B and neutral point D are same. When the jockey contacts a point on the meter wire to the right of D, the potential drop across AD is more than potential drop across AB, which brings the potential of point D less than that of B, hence current flows from B to D in the galvanometer wire.
VERY SHORT ANSWER TYPE QUESTIONS
Q.12. Is the momentum conserved when charge crosses a junction in an electric circuit? Why or why not?
Ans. In the circuit when an electron approaches a junction, in addition to the uniform E that faces it normally (which keep the drift velocity fixed), as drift velocity (vd) is directly proportional to Electric field (E). That’s why there are accumulation of charges on the surface of wires at the junction.
These produce additional electric fields. These fields alter the direction of momentum. Thus, the motion of a charge across junction is not momentum conserving.
Q.13. The relaxation time τ is nearly independent of applied E field whereas it changes significantly with temperature T. First fact is (in part) responsible for Ohm’s law whereas the second fact leads to variation of ρ with temperature. Elaborate why?
Ans. As the drift velocity increases, the relaxation time (τ) (average time between successive collision) decreases which increases the ρ by formula: p = 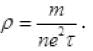
The drift velocity (vd) changes of the order of one mm on increasing electric field, whereas
the drift velocity increases of the order of 102m/s when the number of free electrons (n)
increases on increasing temperature (T). So, due to increase in vd the relaxation time (τ) considerably decreases in metal or conductor.
Q.14. What are the advantages of the null-point method in a Wheat stone bridge? What additional measurements would be required to calculate Runknown by any other method?
Ans. In a Wheatstone bridge the main advantage of null point method is that the resistance of galvanometer does not affect the balance point, there is no need to determine current in resistances and the internal resistance of a galvanometer. It is convenient and easy method for observer.
The R unknown can calculated applying Kirchhoff’s rules to the circuit. We would need additional accurate measurement of all the currents in resistances and galvanometer and internal resistance of the galvanometer.
Important point: The necessary and sufficient condition for balanced Wheatstone bridge is P/Q = R/S
where P and Q are ratio arms and R is known resistance and S is unknown resistance.
Q.15. What is the advantage of using thick metallic strips to join wires in a potentiometer?
Ans. Metallic strips have negligible resistance and need not to be counted in the length l1, of the null point of potentiometer. That’s why the thick metallic strips are used in potentiometer. It is for the convenience of experimenter as he measures only their lengths along the straight segments each of lengths 1 m.
This measurements is done with the help of a centimetre scale or metre scale and leads to the accurate measurements.
Q.16. For wiring in the home, one uses Cu wires or Al wires. What considerations are involved in this?
Ans. For the selection of metal for wiring in home the main criterion are: the availability, conductivity and the cost of the metal.
The Cu wires or Al wires are used for wiring in the home. The main considerations are involved in this process are cost of metal and good conductivity of metal.
Q.17. Why are alloys used for making standard resistance coils?
Ans. Alloys are used for making standard resistance coil because they have low temperature coefficient of resistance with less temperature sensitivity. This keeps the resistance of the wire almost constant even in small temperature change. The alloys also have high resistivity and hence high resistance, because for given length and cross-section area of conductor (L and A are constant).
This keeps the resistance of the wire almost constant even in small temperature change. The alloys also have high resistivity and hence high resistance, because for given length and cross-section area of conductor (L and A are constant).
R α p
Q.18. Power P is to be delivered to a device via transmission cables having resistance RC. If V is the voltage across R and I the current through it, find the power wasted and how can it be reduced.
Ans. As we know that p=VI so, to transmit a constant power P through transmission cable there are two ways:
(i) If a constant power p is transmitted at low voltage (V) and high current (I). In this method high current will produce higher heat by H = I2R and power loss through cable is higher.
(ii) If a constant or same power be transmitted at high voltage (V) and low current. It gives lower loss of power as heat. But need thicker insulation during transmission.
So to transmit high power at long distance, we use low current and high (132 kV) voltage to minimize heat losses through towers and thicket (long) insulator.
To transmit power supply at short distance, we can transmit power at low 440V, 220V, 11KV with higher current.
Q.19. AB is a potentiometer wire (Fig 3.4). If the value of R is increased, in which direction will the balance point J shift?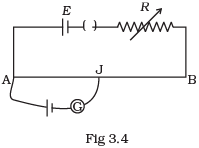 Ans. If the value of R is increased, the current through the wire will decrease which in turn decreases the potential difference across AB, and hence potential gradient (k) across AB decreases.
Ans. If the value of R is increased, the current through the wire will decrease which in turn decreases the potential difference across AB, and hence potential gradient (k) across AB decreases.
Since, at neutral point, for given emf of cell, l increases as potential gradient (k) across AB has decreased because E’ = kl
Thus, with the increase of l, which will result in increase in balance length. So, jockey J will shift towards B.
Q.20. While doing an experiment with potentiometer (Fig 3.5) it was found that the deflection is one sided and (i) the deflection decreased while moving from one end A of the wire to the end B; (ii) the deflection increased. while the jockey was moved towards the end B.
(i) Which terminal +or –ve of the cell E1, is connected at X in case (i) and how is E1 related to E ?
(ii) Which terminal of the cell E1 is connected at X in case (ii)?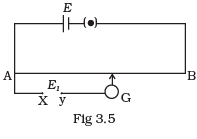 Ans. (i) If the current in auxiliary circuit (lower circuit containing primary cell) decreases, and potential difference across A and jockey/increases. Then deflection in galvanometer is one sided and the deflection decreased, while moving from one end ‘A ’ of the wire to the end ‘S’.
Ans. (i) If the current in auxiliary circuit (lower circuit containing primary cell) decreases, and potential difference across A and jockey/increases. Then deflection in galvanometer is one sided and the deflection decreased, while moving from one end ‘A ’ of the wire to the end ‘S’.
And clearly this is possible only when positive terminal of the cell E1 is connected at X and E1>E.
(ii) If the current in auxiliary circuit increases, and potential difference across A and jockey J increases. Then also deflection in galvanometer is one sided.
And this is possible only when negative terminal of the cell E1 is connected at X.
Q.21. A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation of P.D. across R, verses R.
Ans. We know that 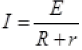 and V=IR.
and V=IR.
So 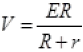 ...(I)
...(I)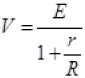 ...(II)
...(II)
Here E, r are constants. So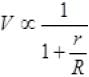 (from II)
(from II)
and V ∝ R (from I)
With increase in R, P.D. across R is increased upto maximum value E.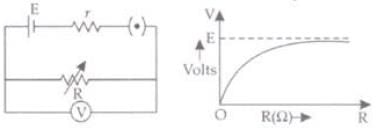
SHORT ANSWER TYPE QUESTIONS
Q.22. First a set of n equal resistors of R each are connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then the n resistors are connected in parallel to the same battery. It is observed that the current is increased 10 times. What is ‘n’?
Ans. When n resistance of each R Ω are connected in series and parallel then
RS = R+R+R+.... n times ⇒ RS = nR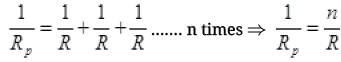
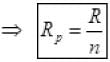
When n resistors are connected in series connected with battery of emf E then current (I) flows. So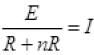 ...(I)
...(I)
And now n resistance are connected in parallel combination then current in circuit increased to 10 times of I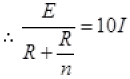
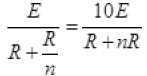
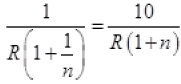
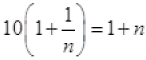
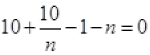
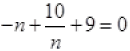 [Multiply by –n to both sides]
[Multiply by –n to both sides]
n2 - 10 - 9n = 0
n2 - 9n - 10 = 0
n2 - 10n + 1n - 10 = 0
n(n-10) + 1(n-10) = 0
So, (n+1) (n-10) = 0
Or n = -1 is not possible or n = 10.
So, there are 10 resistors in combination.
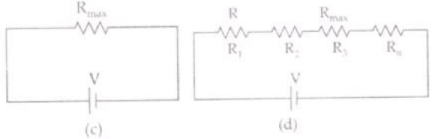
Q.23. Let there be n resistors R1 ............Rn with Rmax = max (R1......... Rn) and Rmin = min {R1 ..... Rn}. Show that when they are connected in parallel, the resultant resistance RP< Rmin and when they are connected in series, the resultant resistance RS > Rmax. Interpret the result physically.
Ans. Let Rmin and Rmax are the minimum and maximum resistances among all resistance R1,R2….Rn.
When resistors are connected in parallel then equivalent resistance
Rp is 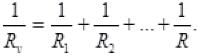
Multiplying both sides by Rmin we get,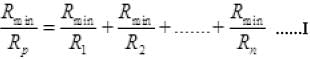
Among R1 R2...., Rn, there must be a resistor which is minimum. So there must be a term 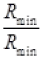 in R.H.S. of equation (I). So R.H.S. in equation (I) must be greater than 1 as all other terms are also positive.
in R.H.S. of equation (I). So R.H.S. in equation (I) must be greater than 1 as all other terms are also positive.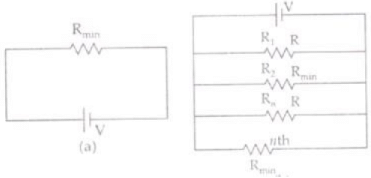
Or 
Or 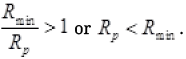
So in parallel combination, the equivalent resistance Rp is always less than any smallest resistance in the combination.
When n resistance are connected in series then equivalent resistance-Rs=R1+R2+R3+.......+Rn. ...(II)
Here, in R.H.S. there must be a term Rmax which has maximum value among R1,R1,........Rn. As all terms R.H.S. of equation II are positive so
RS=R1+R2+R3+..........Rmax +.......+ Rn>Rmax
Or Rs > Rmax
So in series combination equivalent resistance is always greater than the maximum resistance (Rmax) among R1, R2, Rn.
Q.24. The circuit in Fig 3.6 shows two cells connected in opposition to each other. Cell E1 is of emf 6V and internal resistance 2Ω; the cell E2 is of emf 4V and internal resistance 8Ω. Find the potential difference between the points A and B.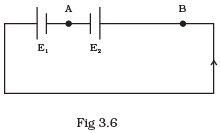 Ans. The above figure can be redrawn as given here. The direction of current in circuit will be as shown in the figure. So point B is at higher potential than A. So VB>VA.
Ans. The above figure can be redrawn as given here. The direction of current in circuit will be as shown in the figure. So point B is at higher potential than A. So VB>VA.
Current (I) in circuit, 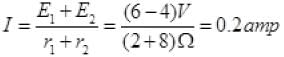
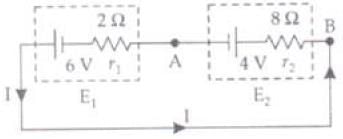
For positive potential A is near to positive terminal of E2 so has +4 V. So potential across E1 and E2: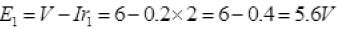
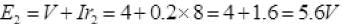
So potential between A and B = E2=5.6 Volt.
As current is flowing from B to A. So potential at B is larger than A.
Q.25. Two cells of same emf E but internal resistance r1 and r2 are connected in series to an external resistor R (Fig 3.7). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.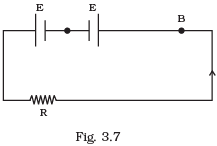 Ans. Current I flowing in the circuit
Ans. Current I flowing in the circuit 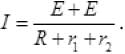
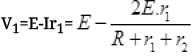
The net potential difference across 1st cell V1 = 0 (Given)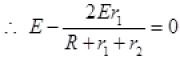
Or 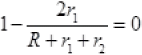
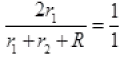
Or 2r1=r1+r2+R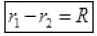
It is the required condition for the potential difference across 1st cell to be zero.
Q.26. Two conductors are made of the same material and have the same length. Conductor A is a solid wire of diameter 1 mm. Conductor B is a hollow tube of outer diameter 2 mm and inner diameter 1 mm. Find the ratio of resistance RA to RB.
Ans.
⇒ 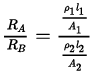
⇒ 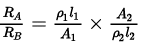
⇒ 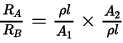
⇒ 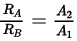
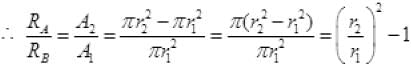
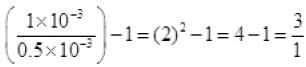
∴ RA : RB = 3:1.
Q.27. Suppose there is a circuit consisting of only resistances and batteries and we have to double (or increase it to n -times) all voltages and all resistances. Show that currents are unaltered. Do this for circuit of Example 3.7 in the NCERT Text Book for Class XII.
Ans. Case I: Consider a circuit having external R1, R2,........, connected with some batteries E1,E2, E3, having their internal resistance r1,r2,r3,
Let the equivalent resistance, emf and internal resistance of above combination is Req, Eeq, and req respectively. So the current passing in the circuit, 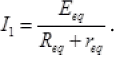
Now the resistance and cells are again connected in a manner that their equivalent resistance, emf and internal resistance are nReq, nEeq and nreq respectively. So again current in new circuit 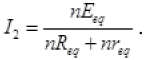
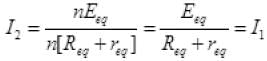
So the current remains same if the R, E and r of a circuits is increased by n times, i.e. nR, nE, nr.
LONG ANSWER TYPE QUESTIONS
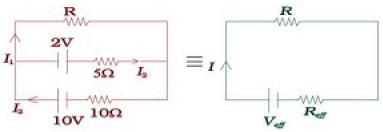
Q.28. Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively, are connected in parallel with the positive end of 10V battery connected to negative pole of 2V battery (Fig 3.8). Find the effective voltage and effective resistance of the combination.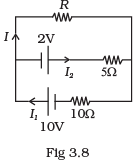 Ans. Applying junction rule at A
Ans. Applying junction rule at A
I1 = I + I2 .................(i)
Apply Kirchhoff’s loop rule on loop BCEF and loop ADEF
10 = IR + 10I1 ...............(2)
2 = 5I2 — IR............(3)
⇒ 2 = 5(I1 — 7) — IR [using (1)]............(4)
multiply (4) by 2, we get
4 = 10I1 - 10I - 2I R ..............(5)
Subtract (5) from (2), we get
⇒ 6 = 3IR + 10I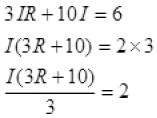
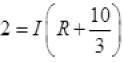 ...........(6)
...........(6)
Let the effective potential difference due to both batteries is Veq. It will be be across resistance R. So
Veq=I(R+Req) ...........(7)
Where Req is the resistance of circuit except R
Comparing (6) and (7)
Veq = 2 Volts and Req =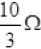
Q.29. A room has AC run for 5 hours a day at a voltage of 220V. The wiring of the room consists of Cu of 1 mm radius and a length of 10 m. Power consumption per day is 10 commercial units. What fraction of it goes in the joule heating in wires? What would happen if the wiring is made of aluminium of the same dimensions?
[ρcu = 1.7 × 10Ωm–8 , ρAl = 2.7 × 10–8 Ωm]
Ans. Total energy consumed in 5 hrs a day by AC and wiring =10 kWh .
∴ Energy consumed in 1 hr by AC and wiring =2 kWh
So total power of AC and wire = 2000 W
P=VI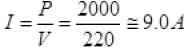
Let P0 is power of wiring then,
P0= I2Rw [Rw=resistance of wiring]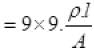
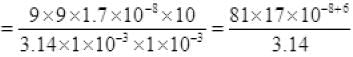
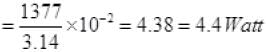
So loss of energy in wiring ≅ 4.4J/sec
The fractional loss due to heating of wires 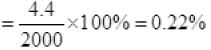
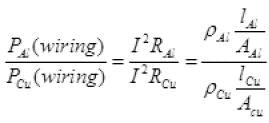 as lAl=lCu and AAl=ACu
as lAl=lCu and AAl=ACu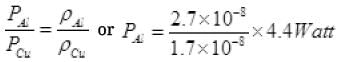
So power loss in Al wiring =7 Watt
The fractional loss due to Al wiring =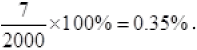
Q.30. In an experiment with a potentiometer, VB = 10V. R is adjusted to be 50Ω (Fig. 3.9). A student wanting to measure voltage E1 of a battery (approx. 8V) finds no null point possible. He then diminishes R to 10Ω and is able to locate the null point on the last (4th) segment of the potentiometer. Find the resistance of the potentiometer wire and potential drop per unit length across the wire in the second case.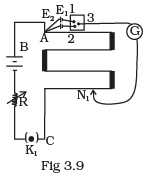
Ans. Let R’ be the resistance of potentiometer wire.
∴ Variable resistance, R=50 Ω
I is the current in primary circuit which is at EB=10V.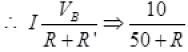 =I (in primary circuit) …I
=I (in primary circuit) …I
Potential difference across the wire of potentiometer
V’=IR’
From I 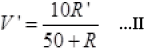
As with R=50 Ω resistance, null point cannot be obtained by 8 Volt.
So, V’< 8 Volt.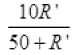 (No balance point)
(No balance point)
As 50+R’ is positive so we can multiply above equation by positive number and we get 10R’<400+8R’
2R’ < 400
R’ < 200 ...III
Similarly, null point obtained by R=10 Ω . Then V”>8 at balance point So it is possible when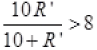 (as from I, R=10)
(as from I, R=10)
Similarly, multiply above equation by positive number 10+R’ to both sides
10R’ > 80 + 8R
2R’ > 80
R’ > 40 ...IV
As the null point is obtained on 4th segment or at 3/4 of total length So at 3/4 R’ (No balance point)
Or 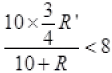 (At balance point)
(At balance point)
So, 7.5R’ < 80+8R
-0.5R’< 80
-R’< 160
R’ > -160
R’ can never be negative so, -160 Ω is considered 160 Ω
So ...V
...V
Any R’ between 160 Ω and 200 Ω will achieve null point. Since the null point is on last 4th segment of potentiometer wire, sothe potential drop across 400cm wire > 8 Volt.
So, k.400cm> 8V (At balance point)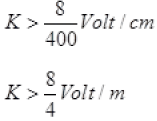
K > 2 Volt/m
As balance point is at 4th wire, so no balance point at 3m,
K.3<8 (No balance point)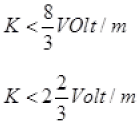
So,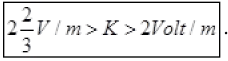
Q.31. (a) Consider circuit in Fig 3.10. How much energy is absorbed by electrons from the initial state of no current (ignore thermal motion) to the state of drift velocity?
(b) Electrons give up energy at the rate of RI2 per second to the thermal energy. What time scale would one associate with energy in problem (a)?
n = no of electron/volume = 1029/m3,
length of circuit = 10 cm,
cross-section = A = (1mm)2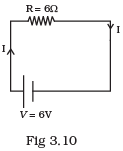 Ans. A = 1 mm2 = 10-6m2
Ans. A = 1 mm2 = 10-6m2
R = 6Ω
n = 1029/m3
V = 6V
e = 1.6 x 10-19C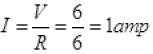
me = 9.1 x 10-31Kg
L = 10cm = 10-1m
(a) ∵ I = Anevd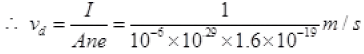
⇒ 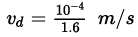
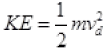 per electron
per electron
Number of electrons (free) in wire = n (volume of wire)
= n x Al
∴ KE of all electrons 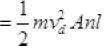
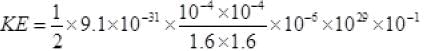
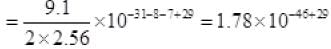
=1.78×10-17J.
So, to start flow of current I, the electrons will take energy from cell
= KE of all electrons= 1.78 x 10-17J
Ans. (b) Loss of energy during current flowing =I2R.
P= 1 x 1 x 6=6 Joule per second
∵ Energy = P.t
Or 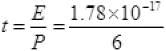
≌ 0.29 x 10-17 sec ≌ 0.3x10-17
= 3 x 10-18 second.
|
74 videos|314 docs|88 tests
|
FAQs on NCERT Exemplars: Current Electricity - Physics Class 12 - NEET
| 1. What is current electricity? |  |
| 2. What is the difference between AC and DC current? |  |
| 3. How is electric current measured? |  |
| 4. What is the relationship between current, voltage, and resistance? |  |
| 5. What are the factors that affect the resistance of a conductor? |  |





















