Measurement of Length and Motion NCERT Solutions | Science for Class 6 PDF Download
Let us enhance our learning
Q1: Some lengths are given in Column I of Table 5.5. Some units are given in Column II. Match the lengths with the units suitable for measuring those lengths.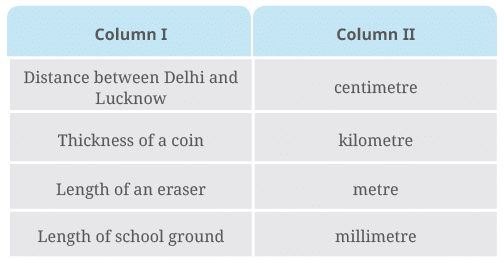 Table 5.5
Table 5.5
Ans:
Q2: Read the following statements and mark True (T) or False (F) against each.
(i) The motion of a car moving on a straight road is an example of linear motion.
Ans: True
(ii) Any object which is changing its position with respect to a reference point with time is said to be in motion.
Ans: True
(iii) 1 km = 100 cm
Ans: False
Q3: Which of the following is not a standard unit of measuring length?
(i) millimetre
(ii) centimetre
(iii) kilometre
(iv) handspan
Ans: (iv) handspan
Q4: Search for the different scales or measuring tapes at your home and school. Find out the smallest value that can be measured using each of these scales. Record your observations in a tabular form.
Ans: Observations of Different Scales or Measuring Tapes: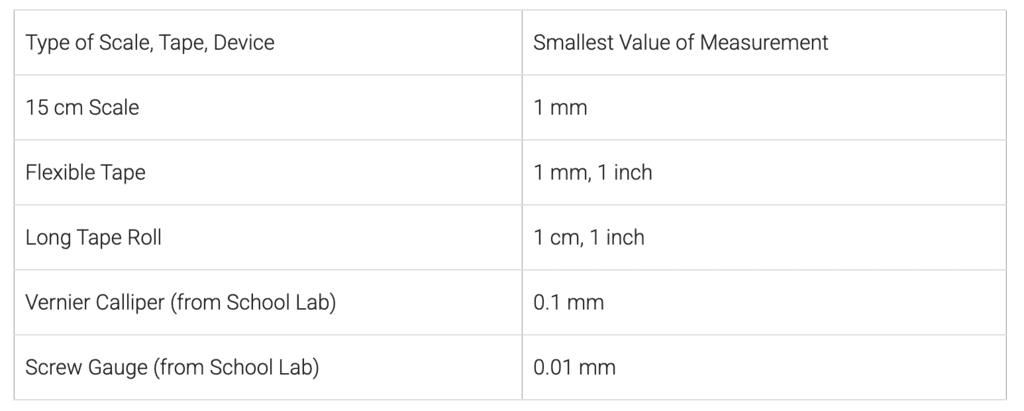
Q5: Suppose the distance between your school and home is 1.5 km. Express it in metres.
Ans: 1.5 km = 1.5 × 1000 = 1500 metres
Q6: Take a tumbler or a bottle. Measure the length of the curved part of the base of glass or bottle and record it.
Ans: Measuring Curved Part of Tumbler/Bottle: Measure the length of the curved part of the base of the tumbler or bottle using a flexible measuring tape and record the value in centimetres or millimetres as per the tape.

Q7: Measure the height of your friend and express it in (i) metres (ii) centimetres and (iii) millimetres.
Ans: If the height of your friend is 1.45 metres:
(i) Metres: 1.45 m
(ii) Centimetres: 145 cm
(iii) Millimetres: 1450 mm
Q8: You are given a coin. Estimate how many coins are required to be placed one after the other lengthwise, without leaving any gap between them, to cover the whole length of the chosen side of a notebook. Verify your estimate by measuring the same side of the notebook and the size of the coin using a 15-cm scale.
Ans:
- Estimate: If the side of the notebook is 30 cm and the coin diameter is 2 cm, you need approximately 15 coins.
- Verification: Measure the actual length of the side of the notebook and the diameter of one coin. Divide the length of the side of the notebook by the diameter of the coin to find the exact number of coins needed.
Q9: Give two examples each for linear, circular and oscillatory motion.
Ans:
- Linear Motion: A car moving on a straight road, a person walking in a straight line.
- Circular Motion: The motion of a fan blade, the motion of a merry-go-round.
- Oscillatory Motion: The swinging of a pendulum, the motion of a child on a swing.
Q10: Observe different objects around you. It is easier to express the lengths of some objects in mm, some in cm and some in m. Make a list of three objects in each category and enter them in the Table 5.6. Ans:
Ans:
Q11: A rollercoaster track is made in the shape shown in Fig. 5.19. A ball starts from point A and escapes through point F. Identify the types of motion of the ball on the rollercoaster and corresponding portions of the track.
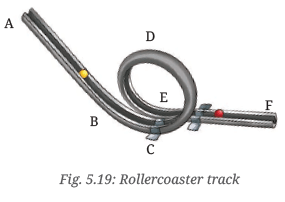 Ans:
Ans:- From A to B: Linear Motion
- From B to C: Curved Motion
- From C to D: Circular Motion
- From D to E: Circular Motion
- From E to F: Linear Motion
Q12: Tasneem wants to make a metre scale by herself. She considers the following materials for it - plywood, paper, cloth, stretchable rubber and steel. Which of these should she not use and why?
Ans: Tasneem should not use stretchable rubber because it can change length when stretched, leading to inaccurate measurements. Plywood, cloth, paper, and steel are more suitable as they maintain consistent lengths.
Q13: Think, design and develop a card game on conversion of units of length to play with your friends.
Ans: Create cards with different lengths and corresponding units (mm, cm, m, km). Each card can have a length in one unit and players must match it to its equivalent in another unit. For example, a card with “100 cm” would match with “1 m”
Intext Questions
Q1. Would it be convenient to use the unit metre to measure larger lengths, such as the length of a railway track between two cities, or to measure smaller lengths, such as the thickness of a page of a book? (Page 83)
Ans: Length and distance measurements are given in units and the number of units. For long distances, if small units like meters are used, the number of units will be very large. This becomes inconvenient. Therefore, long distances like distances among two cities are measured in kilometres.
Small thicknesses or lengths like the thickness of a page of a book are measured in very small units like mm. If this is measured in metres or km then several units become a very small fraction, inconvenient to handle.
Q2. What do such kilometre stones indicate? How could Padma conclude that she was getting closer to her destination? (Page 89)
Ans: Kilometre stones on the roads between cities and places indicate the distance left to reach a place or city (the reference point). Padma saw that the earlier kilometre stone showed the distance to Delhi as 70 km and the next kilometre stone showed the distance to Delhi as 60 km. She concluded that she was in motion and moving towards Delhi (the reference point concerning which she was changing her position with time).
Q3.Does this mean that the position of Padma, with respect to the reference point, is changing with time? When does the position of an object change with respect to a reference point? Does it change when an object is moving? (Page 89)
Ans:
- Padma saw from the kilometre stones that the distance to Delhi is decreasing with time. This means that with respect to Delhi (reference point here), she was changing position with time.
- When the position of an object changes with time with respect to a reference point, the object is said to be in a state of motion or is moving.
- Padma was changing her position with time with respect to Delhi, means that she was moving closer and closer to Delhi with time.
|
68 videos|260 docs|27 tests
|
FAQs on Measurement of Length and Motion NCERT Solutions - Science for Class 6
| 1. How can we measure length accurately? |  |
| 2. What is the difference between distance and displacement? |  |
| 3. How do we calculate speed using the formula? |  |
| 4. What is the difference between speed and velocity? |  |
| 5. Why is it essential to measure length accurately in scientific experiments? |  |

















