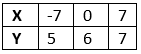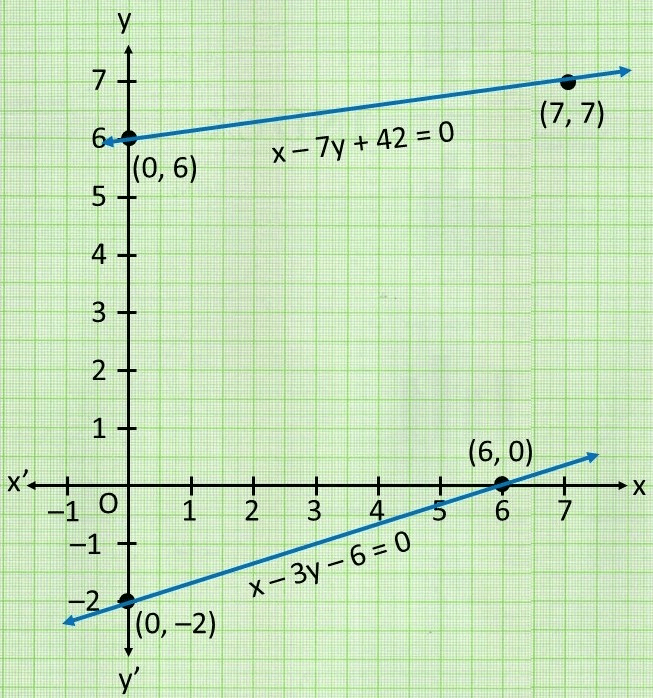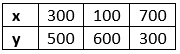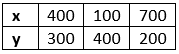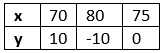NCERT Solutions for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables (Exercise 3.1)
Q1. Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting?) Represent this situation algebraically and graphically.
Let the present age of Aftab be ‘x’.
And, the present age of his daughter be ‘y’.
Now, we can write, seven years ago,
- Age of Aftab = x - 7
- Age of his daughter = y - 7
According to the question, x − 7 = 7(y − 7)
⇒ x − 7 = 7y − 49
⇒ x − 7y = −42 ………………………(i)
Also, three years from now or after three years:
- Age of Aftab will become = x + 3.
- Age of his daughter will become = y + 3
According to the situation given:
x + 3 = 3(y + 3)
⇒ x + 3 = 3y + 9
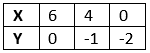
⇒ x − 3y = 6 …………..…………………(ii)
Subtracting equation (i) from equation (ii) we have:
(x − 3y) − (x − 7y) = 6 − (−42)
⇒ −3y + 7y = 6 + 42
⇒ 4y = 48
⇒ y = 12
The algebraic equation is represented by:
x − 7y = −42
x − 3y = 6
For, x − 7y = −42 or x = −42 + 7y
The solution table is
For, x − 3y = 6 or x = 6 + 3y
The solution table is
The graphical representation is:
Q2. The coach of a cricket team buys 3 bats and 6 balls for Rs.3900. Later, she buys another bat and 3 more balls of the same kind for Rs.1300. Represent this situation algebraically and geometrically.
Let us assume that the cost of a bat be ‘Rs x’
And, the cost of a ball be ‘Rs y’
According to the question, the algebraic representation is:
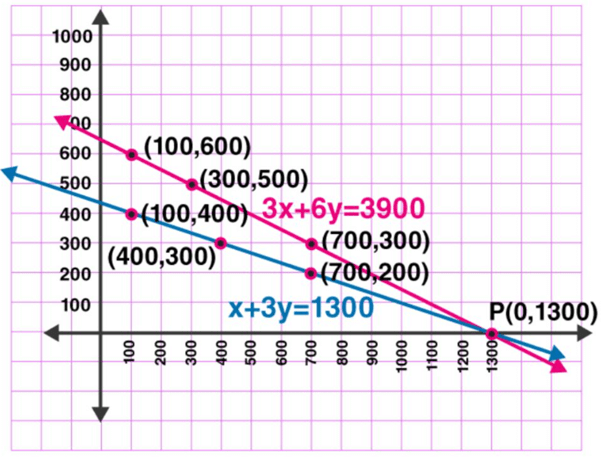
3x + 6y = 3900
And x + 3y = 1300
For, 3x + 6y = 3900
Or x = (3900 - 6y) / 3
The solution table is:
For, x + 3y = 1300
Or x = 1300 - 3y
The solution table is:
The graphical representation is as follows:
Q3. The cost of 2 kg of apples and 1kg of grapes on a day was found to be Rs.160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs.300. Represent the situation algebraically and geometrically.
Let the cost of 1 kg of apples be ‘Rs. x’
And, cost of 1 kg of grapes be ‘Rs. y’
According to the question, the algebraic representation is:
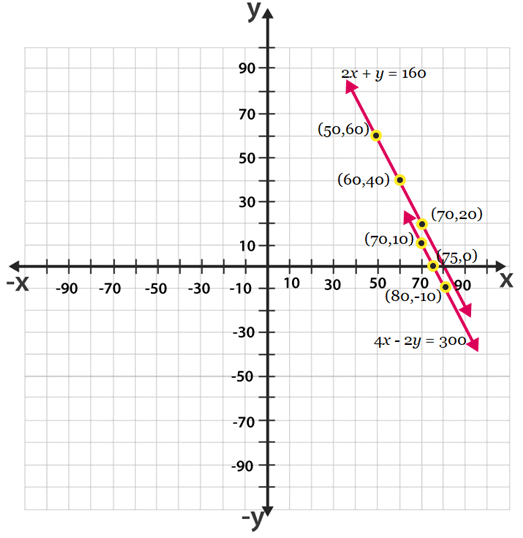
2x + y = 160 And 4x + 2y = 300
For, 2x + y = 160 or y = 160 − 2x, the solution table is:
For 4x + 2y = 300 or y = (300 - 4x) / 2, the solution table is:
The graphical representation is as follows:
Check out the NCERT Solutions of all the exercises of Linear Equations in Two Variables:
- Ex 3.2 NCERT Solutions: Pair of Linear Equations in Two Variables
- Ex 3.3 NCERT Solutions: Pair of Linear Equations in Two Variables
- Ex 3.4 NCERT Solutions: Pair of Linear Equations in Two Variables
- Ex 3.5 NCERT Solutions: Pair of Linear Equations in Two Variables
- Ex 3.6 NCERT Solutions: Pair of Linear Equations in Two Variables
|
70 videos|242 docs|187 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables (Exercise 3.1)
| 1. What are linear equations in two variables? |  |
| 2. How do we solve a pair of linear equations in two variables? |  |
| 3. What is the importance of linear equations in two variables in real-life applications? |  |
| 4. Can a pair of linear equations in two variables have more than one solution? |  |
| 5. How does the graphical method of solving a pair of linear equations work? |  |