NCERT Solutions Class 12 Chemistry Chapter 1 - Solutions
Q1.3: Define the following terms:
(a) Mole fraction
(b) Molality
(c) Molarity
(d) Mass percentage.
Ans:
(a) Mole fraction
The mole fraction of a component in a mixture is defined as the ratio of the number of moles of the component to the total number of moles of all the components in the mixture.
i.e.,
Mole fraction of a component
Mole fraction is denoted by ‘x’.
If in a binary solution, the number of moles of the solute and the solvent are nA and nB respectively, then the mole fraction of the solute in the solution is given
by,
Similarly, the mole fraction of the solvent in the solution is given as:
(b) Molality
Molality (m) is defined as the number of moles of the solute per kilogram of the
solvent. It is expressed as:
Molality (m)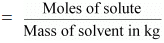
(c) Molarity
Molarity (M) is defined as the number of moles of the solute dissolved in one Litre of the solution.
It is expressed as:
Molarity (M)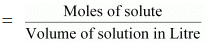
(d) Mass percentage
The mass percentage of a component of a solution is defined as the mass of the solute in grams present in 100 g of the solution. It is expressed as:
Mass % of a component
Q1.4: Concentrated nitric acid used in laboratory work is 68% nitric acid by mass in aqueous solution. What should be the molarity of such a sample of the acid if the density of the solution is 1.504 g mL−1?
Ans: Concentrated nitric acid used in laboratory work is 68% nitric acid by mass in an aqueous solution. This means that 68 g of nitric acid is dissolved in 100 g of the solution.
Molar mass of nitric acid (HNO3) = 1 × 1 + 1 × 14 + 3 × 16 = 63 g mol−1
Then, number of moles of HNO3 = 68/63 mol = 1.079 mol
Given,
Density of solution = 1.504 g mL−1
Volume of 100 g solution = 100 / 1.504 mL
= 66.49 mL
= 66.49 × 10-3 mL
Molarity of solution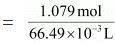
= 16.23 M
Q1.5: A solution of glucose in water is labelled as 10% w/w, what would be the molality and mole fraction of each component in the solution? If the density of solution is 1.2 g mL−1, then what shall be the molarity of the solution?
Ans: 10% w/w solution of glucose in water means that 10 g of glucose in present in 100 g of the solution i.e., 10 g of glucose is present in (100 − 10) g = 90 g of water.
Molar mass of glucose (C6H12O6) = 6 × 12 + 12 × 1 + 6 × 16 = 180 g mol−1
Then, number of moles of glucose = 10/180 mol = 0.056 mol
Molality of solution = 0.056 mol / 0.09 kg = 0.62 m
Number of moles of water = 90g / 18g mol-1 = 5 mol
Mole fraction of glucose (xg)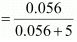
= 0.011
And, mole fraction of water xw = 1 - xg
= 1 − 0.011 = 0.989
If the density of the solution is 1.2 g mL−1, then the volume of the 100 g solution can be given as:
∴ Molarity of the solution
= 0.67 M
Q1.6: How many mL of 0.1 M HCl are required to react completely with 1 g mixture of Na2CO3 and NaHCO3 containing equimolar amounts of both?
Ans: 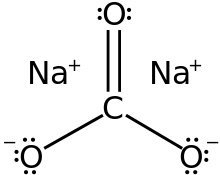 Structure of Na2CO3
Structure of Na2CO3
Let the amount of Na2CO3 in the mixture be x g.
Then, the amount of NaHCO3 in the mixture is (1 − x) g.
Molar mass of Na2CO3 = 2 × 23 + 1 × 12 + 3 × 16 = 106 g mol−1
Number of moles Na2CO3 = x / 106 mol
Molar mass of NaHCO3 = 1 × 23 + 1 × 12 + 3 × 16 = 84 g mol−1
Number of moles of NaHCO3 = 1 -x /84 mol
According to the question,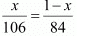
⇒ 84x = 106 − 106x
⇒ 190x = 106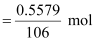
⇒ x = 0.5579
Therefore, number of moles of Na2CO3 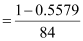
= 0.0053 mol
And, number of moles of NaHCO3
= 0.0053 mol
HCl reacts with Na2CO3 and NaHCO3 according to the following equation.
1 mol of Na2CO3 reacts with 2 mol of HCl.
Therefore, 0.0053 mol of Na2CO3 reacts with 2 × 0.0053 mol = 0.0106 mol.
Similarly, 1 mol of NaHCO3 reacts with 1 mol of HCl.
Therefore, 0.0053 mol of NaHCO3 reacts with 0.0053 mol of HCl.
Total moles of HCl required = (0.0106 + 0.0053) mol
= 0.0159 mol
In 0.1 M of HCl,
0.1 mol of HCl is present in 1000 mL of the solution.
Therefore, 0.0159 mol of HCl is present in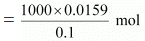
= 159 mL of the solution
Hence, 159 mL of 0.1 M of HCl is required to react completely with 1 g mixture of Na2CO3 and NaHCO3, containing equimolar amounts of both.
Q1.7: A solution is obtained by mixing 300 g of 25% solution and 400 g of 40% solution by mass. Calculate the mass percentage of the resulting solution.
Ans: Total amount of solute present in the mixture is given by,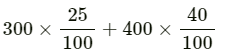
= 75 + 160
= 235g
Total amount of solution = 300 + 400 = 700 g
Therefore, mass percentage (w/w) of the solute in the resulting solution = 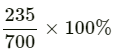
= 33.57%
And, mass percentage (w/w) of the solvent in the resulting solution,
= (100 − 33.57)%
= 66.43%
Q1.8: An antifreeze solution is prepared from 222.6 g of ethylene glycol (C2H6O2) and 200 g of water. Calculate the molality of the solution. If the density of the solution is 1.072 g mL−1, then what shall be the molarity of the solution?
Ans: Molar mass of ethylene glycol [C2H4(OH)2] = 2 × 12 + 6 × 1 + 2 ×16 = 62 gmol−1
Number of moles of ethylene glycol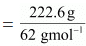
= 3.59 mol
Therefore, molality of the solution = 3.59 MOL / 0.200 kg = 17.95 m
Total mass of the solution = (222.6 + 200) g = 422.6 g
Given,
Density of the solution = 1.072 g mL−1
Volume of the solution = 422.6 g / 1.072g mL-1
= 394.22 mL
= 0.3942 × 10−3 L
⇒ Molarity of the solution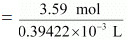
= 9.11 M
Q1.9: A sample of drinking water was found to be severely contaminated with chloroform (CHCl3) supposed to be a carcinogen. The level of contamination was 15 ppm (by mass):
(a) express this in percent by mass
(b) determine the molality of chloroform in the water sample.
Ans:
(a) 15 ppm (by mass) means 15 parts per million (106) of the solution.
Therefore, percent by mass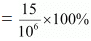
= 1.5 × 10−3 %
(b) Molar mass of chloroform (CHCl3) = 1 × 12 + 1 × 1 + 3 × 35.5
= 119.5 g mol−1
Now, according to the question,
15 g of chloroform is present in 106 g of the solution.
i.e., 15 g of chloroform is present in (106 − 15) ≈ 106 g of water.
Molality of the solution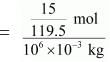
= 1.26 × 10−4 m
Q1.10: What role does the molecular interaction play in a solution of alcohol and water?
Ans: In pure alcohol and water, the molecules are held tightly by a strong hydrogen bonding. The interaction between the molecules of alcohol and water is weaker than alcohol−alcohol and water−water interactions. As a result, when alcohol and water are mixed, the intermolecular interactions become weaker and the molecules can easily escape. This increases the vapour pressure of the solution, which in turn lowers the boiling point of the resulting solution.
Q1.11: Why do gases always tend to be less soluble in liquids as the temperature is raised?
Ans: Solubility of gases in liquids decreases with an increase in temperature. This is because dissolution of gases in liquids is an exothermic process.
Gas + Liquid → Solution + Heat
Therefore, when the temperature is increased, heat is supplied and the equilibrium shifts backwards, thereby decreasing the solubility of gases.
Q1.12: State Henry’s law and mention some important applications?
Ans: Henry’s law states that partial pressure of a gas in the vapour phase is proportional to the mole fraction of the gas in the solution. If p is the partial pressure of the gas in the vapour phase and x is the mole fraction of the gas, then Henry’s law can be expressed as:
p = KH x
Where,
KH is Henry’s law constant
Some important applications of Henry’s law are mentioned below.
(a) Bottles are sealed under high pressure to increase the solubility of CO2 in soft drinks and soda water.
(b) Henry’s law states that the solubility of gases increases with an increase in pressure. Therefore, when a scuba diver dives deep into the sea, the increased sea pressure causes the nitrogen present in air to dissolve in his blood in great amounts. As a result, when he comes back to the surface, the solubility of nitrogen again decreases and the dissolved gas is released, leading to the formation of nitrogen bubbles in the blood. This results in the blockage of capillaries and leads to a medical condition known as ‘bends’ or ‘decompression sickness’.
Hence, the oxygen tanks used by scuba divers are filled with air and diluted with helium to avoid bends.
(c) The concentration of oxygen is low in the blood and tissues of people living at high altitudes such as climbers. This is because at high altitudes, partial pressure of oxygen is less than that at ground level. Low-blood oxygen causes climbers to become weak and disables them from thinking clearly. These are symptoms of anoxia.
Q1.13: The partial pressure of ethane over a solution containing 6.56 × 10−3 g of ethane is 1 bar. If the solution contains 5.00 × 10−2 g of ethane, then what shall be the partial pressure of the gas?
Ans:
Molar mass of ethane (C2H6) = 2 × 12 + 6 × 1 = 30 g mol−1
Number of moles present in 6.56 × 10−2 g of ethane = 6.56 × 10-3 / 30
= 2.187 × 10−3 mol
Let the number of moles of the solvent be x.
According to Henry’s law,
p = KHx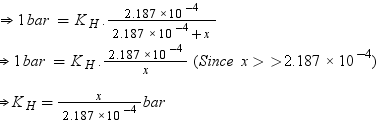
Number of moles present in 5.00 × 10−2 g of ethane = 5.00 × 10-2 /30 mol
= 1.67 × 10−3 mol
According to Henry’s law,
p = KHx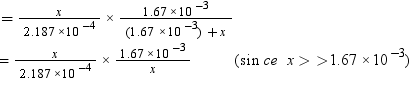
= 7.636 bar
Hence, partial pressure of the gas shall be 7.636 bar.
Q1.14: What is meant by positive and negative deviations from Raoult's law and how is the sign of Δsol H related to positive and negative deviations from Raoult's law?
Ans: According to Raoult’s law, the partial vapour pressure of each volatile component in any solution is directly proportional to its mole fraction. The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The solutions that do not obey Raoult’s law (non-ideal solutions) have vapour pressures either higher or lower than that predicted by Raoult’s law. If the vapour pressure is higher, then the solution is said to exhibit positive deviation, and if it is lower, then the solution is said to exhibit negative deviation from Raoult’s law.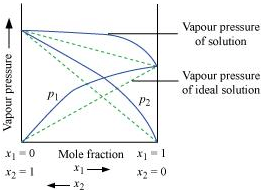 Vapour pressure of a two-component solution showing positive deviation from Raoult’s law
Vapour pressure of a two-component solution showing positive deviation from Raoult’s law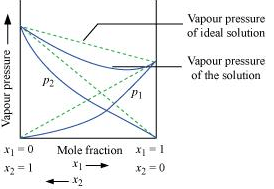 Vapour pressure of a two-component solution showing negative deviation from Raoult’s law
Vapour pressure of a two-component solution showing negative deviation from Raoult’s law
In the case of an ideal solution, the enthalpy of the mixing of the pure components for forming the solution is zero.
ΔsolH = 0
In the case of solutions showing positive deviations, absorption of heat takes place.
∴ ΔsolH = Positive
In the case of solutions showing negative deviations, evolution of heat takes place.
∴ ΔsolH = Negative
Q1.15: An aqueous solution of 2% non-volatile solute exerts a pressure of 1.004 bar at the normal boiling point of the solvent. What is the molar mass of the solute?
Ans: Here,
Vapour pressure of the solution at normal boiling point (p1) = 1.004 bar
Vapour pressure of pure water at normal boiling point (p°1) = 1.013 bar
Mass of solute, (w2) = 2 g
Mass of solvent (water), (w1) = 98 g
Molar mass of solvent (water), (M1) = 18 g mol−1
According to Raoult’s law,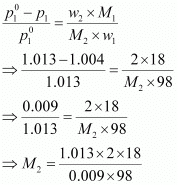
= 41.35 g mol−1
Hence, the molar mass of the solute is 41.35 g mol−1.
Q1.16: Heptane and octane form an ideal solution. At 373 K, the vapour pressures of the two liquid components are 105.2 kPa and 46.8 kPa respectively. What will be the vapour pressure of a mixture of 26.0 g of heptane and 35 g of octane?
Ans: Vapour pressure of heptane (p°1) = 105.2 kPa
Vapour pressure of octane (p°2) = 46.8 kPa
We know that,
Molar mass of heptane (C7H16) = 7 × 12 + 16 × 1
= 100 g mol−1
Number of moles of heptane = 26 / 100 mol
= 0.26 mol
Molar mass of octane (C8H18) = 8 × 12 + 18 × 1
= 114 g mol−1
Number of moles of octane = 35/114 mol
= 0.31 mol
Mole fraction of heptane, x1 = 0.26 /(0.26 + 0.31)
= 0.456
And, mole fraction of octane, x2 = 1 − 0.456
= 0.544
Now, partial pressure of heptane, p1 = x1p10
= 0.456 × 105.2
= 47.97 kPa
Partial pressure of octane,
= 0.544 × 46.8
= 25.46 kPa
Hence, vapour pressure of solution, ptotal = p1 + p2
= 47.97 + 25.46
= 73.43 kPa
Q1.17: The vapour pressure of water is 12.3 kPa at 300 K. Calculate vapour pressure of 1 molal solution of a non-volatile solute in it.
Ans: 1 molal solution means 1 mol of the solute is present in 1000 g of the solvent (water).
Molar mass of water = 18 g mol−1
Number of moles present in 1000 g of water = 1000/18
= 55.56 mol
Therefore, mole fraction of the solute in the solution is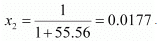
It is given that,
Vapour pressure of water, p°1 = 12.3 kPa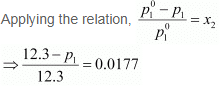
⇒ 12.3 − p1 = 0.2177
⇒ p1 = 12.0823
= 12.08 kPa (approximately)
Hence, the vapour pressure of the solution is 12.08 kPa.
Q1.18: Calculate the mass of a non-volatile solute (molar mass 40 g mol−1) which should be dissolved in 114 g octane to reduce its vapour pressure to 80%.
Ans: Let the vapour pressure of pure octane be p°1
Then, the vapour pressure of the octane after dissolving the non-volatile solute is 80/100 p°1 = 0.8 p°1.
Molar mass of solute, M2 = 40 g mol−1
Mass of octane, w1 = 114 g
Molar mass of octane, (C8H18), M1 = 8 × 12 + 18 × 1
= 114 g mol−1
Applying the relation,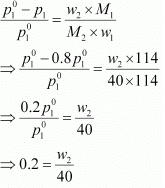
⇒ w2 = 8 g
Hence, the required mass of the solute is 8 g.
Q1.19: A solution containing 30 g of non-volatile solute exactly in 90 g of water has a vapour pressure of 2.8 kPa at 298 K. Further, 18 g of water is then added to the solution and the new vapour pressure becomes 2.9 kPa at 298 K. Calculate:
(i) molar mass of the solute
(ii) vapour pressure of water at 298 K.
Ans:
(i) Let, the molar mass of the solute be M g mol−1
Now, the no. of moles of solvent (water), 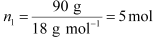
And, the no. of moles of solute, 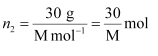
p1 = 2.8kPa
Applying the relation:
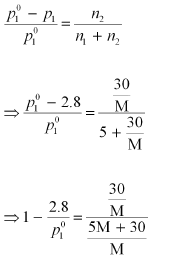
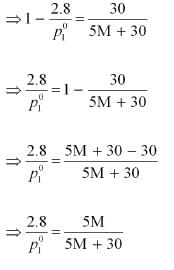
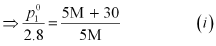
After the addition of 18 g of water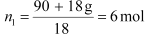
p1 = 2.9kPa
Again, applying the relation: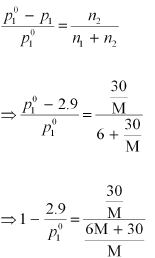
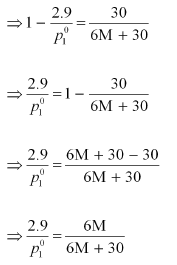
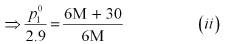
Dividing equation (i) by (ii), we have: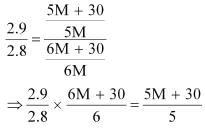
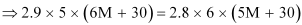
⇒ 87 M + 435 = 84 M + 504
⇒ 3 M = 69
⇒ M = 23 u
Therefore, the molar mass of the solute is 23 g mol−1.
(ii) Putting the value of ‘M’ in equation (i), we have:
Hence, the vapour pressure of water at 298 K is 3.53 kPa.
Q1.20: A 5% solution (by mass) of cane sugar in water has freezing point of 271 K. Calculate the freezing point of 5% glucose in water if freezing point of pure water is 273.15 K.
Ans:
 Fig: Structure of sugarcane
Fig: Structure of sugarcane
Here, ΔTf = (273.15 − 271) K = 2.15 K
Molar mass of sugar (C12H22O11) = 12 × 12 + 22 × 1 + 11 × 16 = 342 g mol−1
5% solution (by mass) of cane sugar in water means 5 g of cane sugar is present in (100 − 5)g = 95 g of water.
Now, number of moles of cane sugar = 5 / 342 mol = 0.0146 mol
Therefore, molality of the solution, m = 0.0146 mol / 0.095 kg = 0.1537 mol kg−1
Applying the relation,
ΔTf = Kf × m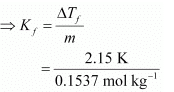
= 13.99 K kg mol−1
Molar of glucose (C6H12O6) = 6 × 12 + 12 × 1 + 6 × 16 = 180 g mol−1
5% glucose in water means 5 g of glucose is present in (100 − 5) g = 95 g of water.
Number of moles of glucose = 5 / 180 mol = 0.0278 mol
Therefore, molality of the solution, m = 0.0278 mol / 0.095 kg = 0.2926 mol kg−1
Applying the relation,
ΔTf = Kf × m
= 13.99 K kg mol−1 × 0.2926 mol kg−1
= 4.09 K (approximately)
Hence, the freezing point of 5% glucose solution is (273.15 − 4.09) K= 269.06 K.
Q1.21: Two elements A and B form compounds having formula AB2 and AB4. When dissolved in 20 g of benzene (C6H6), 1 g of AB2 lowers the freezing point by 2.3 K whereas 1.0 g of AB4 lowers it by 1.3 K. The molar depression constant for benzene is 5.1 Kkg mol−1. Calculate atomic masses of A and B.
Ans: We know that,
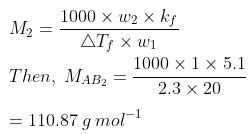
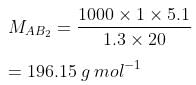
Now, we have the molar masses of AB2 and AB4 as 110.87 g mol−1 and 196.15 g mol−1 respectively.
Let the atomic masses of A and B be x and y respectively.
Now, we can write
x + 2y = 110.81 .... (1)
x + 4y = 196.15 .... (2)
Subtracting equation (i) from (ii), we have
2y = 85.28
⇒ y = 42.64
Putting the value of ‘y’ in equation (1), we have
x + 2 × 42.64 = 110.87
⇒ x = 25.59
Hence, the atomic masses of A and B are 25.59 u and 42.64 u respectively.
Q1.22: At 300 K, 36 g of glucose present in a litre of its solution has an osmotic pressure of 4.98 bar. If the osmotic pressure of the solution is 1.52 bars at the same temperature, what would be its concentration?
Ans: Here,
T = 300 K
π = 1.52 bar
R = 0.083 bar L K−1 mol−1
Applying the relation,
π = CRT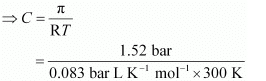
= 0.061 mol
Since the volume of the solution is 1 L, the concentration of the solution would be 0.061 M.
Q1.23: Suggest the most important type of intermolecular attractive interaction in the following pairs.
(i) n-hexane and n-octane
(ii) I2 and CCl4
(iii) NaClO4 and water
(iv) methanol and acetone
(v) acetonitrile (CH3CN) and acetone (C3H6O).
Ans:
(i) Van der Waal’s forces of attraction.
(ii) Van der Waal’s forces of attraction.
(iii) Ion-dipole interaction.
(iv) Dipole-dipole interaction.
(v) Dipole-dipole interaction.
Q1.24: Based on solute-solvent interactions, arrange the following in order of increasing solubility in n-octane and explain. Cyclohexane, KCl, CH3OH, CH3CN.
Ans: n-octane is a non-polar solvent. Therefore, the solubility of a non-polar solute is more than that of a polar solute in the n-octane.
The order of increasing polarity is:
Cyclohexane < CH3CN < CH3OH < KCl
Therefore, the order of increasing solubility is:
KCl < CH3OH < CH3CN < Cyclohexane
Q1.25: Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?
(i) Phenol
(ii) Toluene
(iii) Formic acid
(iv) Ethylene glycol
(v) Chloroform
(vi) Pentanol.
Ans:
(i) Phenol (C6H5OH) has the polar group −OH and non-polar group −C6H5. Thus, phenol is partially soluble in water.
(ii) Toluene (C6H5−CH3) has no polar groups. Thus, toluene is insoluble in water.
(iii) Formic acid (HCOOH) has the polar group −OH and can form H-bond with water. Thus, formic acid is highly soluble in water.
(iv) Ethylene glycol 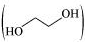 has polar −OH group and can form H−bond. Thus, it is highly soluble in water.
has polar −OH group and can form H−bond. Thus, it is highly soluble in water.
(v) Chloroform is insoluble in water.
(vi) Pentanol (C5H11OH) has polar −OH group, but it also contains a very bulky non-polar −C5H11 group. Thus, pentanol is partially soluble in water.
Q1.26: If the density of some lake water is 1.25 g mL−1 and contains 92 g of Na ions per kg of water, calculate the molality of Na ions in the lake.
Ans: Number of moles present in 92 g of Na+ ions = 92g / 23g mol-1 = 4 mol
Therefore, molality of Na + ions in the lake = 4 mol / 1 kg = 4 m
Q1.27: If the solubility product of CuS is 6 × 10−16, calculate the maximum molarity of CuS in aqueous solution.
Ans: Solubility product of CuS, Ksp = 6 × 10−16
Let s be the solubility of CuS in mol L−1.
CuS ↔ Cu2+ + S2-
s s
Now K_(sp) = [Cu2+][S2-]
= sxs
=s2
Then, we have, Ksp = s2 = 6 x10-16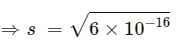
= 2.45 × 10−8 mol L−1
Hence, the maximum molarity of CuS in an aqueous solution is 2.45 × 10−8 mol L−1.
Q1.28: Calculate the mass percentage of aspirin (C9H8O4) in acetonitrile (CH3CN) when 6.5 g of C9H8O4 is dissolved in 450 g of CH3CN.
Ans: 6.5 g of C9H8O4 is dissolved in 450 g of CH3CN.
Then, total mass of the solution = (6.5 + 450) g = 456.5 g
Therefore, mass percentage of C9H8O4 = (6.5/456.5) × 100% = 1.424%
Q1.29: Nalorphene (C19H21NO3), similar to morphine, is used to combat withdrawal symptoms in narcotic users. Dose of nalorphene generally given is 1.5 mg. Calculate the mass of 1.5 × 10−3m aqueous solution required for the above dose.
Ans: The molar mass of nalorphene (C19H21NO3) is given as
19 x 12 + 21 x 1 + 1 x 14 + 3 x 16 = 311 gmol-1
In 1.5 × 10−3m aqueous solution of nalorphene,
1 kg (1000 g) of water contains 1.5 × 10−3 mol = 1.5 x 10-3 x 311 g
= 0.4665 g
Therefore, total mass of the solution = (1000 + 0.4665)g
= 1000.4665 g
This implies that the mass of the solution containing 0.4665 g of nalorphene is 1000.4665 g.
Therefore, mass of the solution containing 1.5 mg of nalorphene is: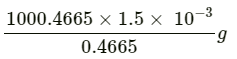
= 3.22 g
Hence, the mass of aqueous solution required is 3.22 g.
Q1.30: Calculate the amount of benzoic acid (C6H5COOH) required for preparing 250 mL of 0.15 M solution in methanol.
Ans: 0.15 M solution of benzoic acid in methanol means,
1000 mL of solution contains 0.15 mol of benzoic acid
Therefore, 250 mL of solution contains =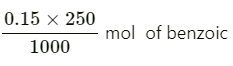
= 0.0375 mol of benzoic acid
Molar mass of benzoic acid (C6H5COOH) = 7 × 12 + 6 × 1 + 2 × 16
= 122 g mol−1
Hence, required benzoic acid = 0.0375 mol × 122 g mol−1
= 4.575 g
Q1.31: The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the order given above. Explain briefly.
Ans: Among H, Cl, and F, H is least electronegative while F is most electronegative. Then, F can withdraw electrons towards itself more than Cl and H. Thus, trifluoroacetic acid can easily lose H ions i.e., trifluoroacetic acid ionizes to the largest extent. Now, the more ions produced, the greater is the depression of the freezing point. Hence, the depression in the freezing point increases in the order:
Acetic acid < trichloroacetic acid < trifluoroacetic acid
Q1.32: Calculate the depression in the freezing point of water when 10 g of CH3CH2CHClCOOH is added to 250 g of water. Ka = 1.4 × 10−3, Kf = 1.86 K kg mol−1.
Ans: Molar mass of CH3CH2CHClCOOH = 15 + 14 + 13 + 35.5 + 12 + 16 + 16 + 1 = 122.5 g mol-1
∴ No. of moles present in 10 g of CH3CH2CHClCOOH
= 0.0816mol
It is given that 10 g of CH3CH2CHClCOOH is added to 250 g of water.
∴ Molality of the solution,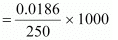
= 0.3264 mol kg-1
Let α be the degree of dissociation of CH3CH2CHClCOOH undergoes dissociation according to the following equation: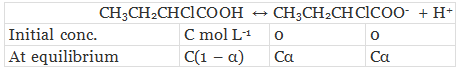
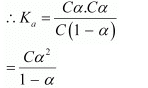
Since α is very small with respect to 1, 1 − α ≈ 1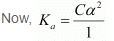
⇒ Ka = Cα2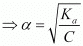

= 0.0655
Again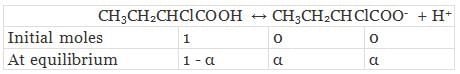
Total moles of equilibrium = 1 − α + α + α
= 1 + α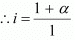
Hence, the depression in the freezing point of water is given as:
ΔTf = i.Kfm
= 1.0655 × 1.86 K kg mol-1 × 0.3264 mol kg-1
= 0.65 K
Q1.33: 19.5 g of CH2FCOOH is dissolved in 500 g of water. The depression in the freezing point of water observed is 1.0°C. Calculate the van’t Hoff factor and dissociation constant of fluoroacetic acid.
Ans: It is given that: w1 = 500g
w2 = 19.5g
Kf = 1.86 K kg mol-1
ΔTf = 1 K
We know that:
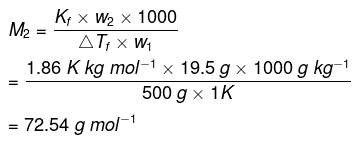
Therefore, observed molar mass of
CH2FCOOH, (M2)obs = 72.54 g mol
The calculated molar mass of CH2FCOOH is:
(M2)cal = 14 + 19 + 12 + 16 + 16 + 1
=78 g mol-1
Therefore,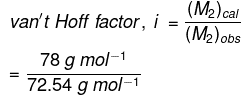
=1.0753
Let α be the degree of dissociation of CH2FCOOH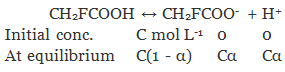
Total = C(1 + α)
⇒ i = 1 + α
⇒ α = i - 1
= 1.0753 - 1
= 0.0753
Now, the value of Ka is given as:
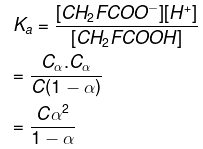
Taking the volume of the solution as 500 mL, we have the concentration: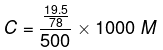
= 0.5 M
Therefore,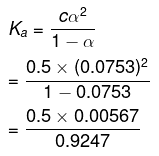
= 0.00307 (approximately)
= 3.07 × 10-3
Q1.34: Vapour pressure of water at 293 K is 17.535 mm Hg. Calculate the vapour pressure of water at 293 K when 25 g of glucose is dissolved in 450 g of water.
Ans: Vapour pressure of water, p°1 = 17.535 mm of Hg
Mass of glucose, w2 = 25 g
Mass of water, w1 = 450 g
We know that,
Molar mass of glucose (C6H12O6), M2 = 6 × 12 + 12 × 1 + 6 × 16
= 180 g mol−1
Molar mass of water, M1 = 18 g mol−1
Then, number of moles of glucose,
= 0.139 mol
And, number of moles of water,
= 25 mol
We know that,
⇒ p1 = 17.44 mm of Hg
Hence, the vapour pressure of water is 17.44 mm of Hg.
Q1.35: Henry’s law constant for the molality of methane in benzene at 298 Kis 4.27 × 105 mm Hg. Calculate the solubility of methane in benzene at 298 Kunder 760 mm Hg.
Ans: Here,
p = 760 mm Hg
kH = 4.27 × 105 mm Hg
According to Henry’s law,
p = kHx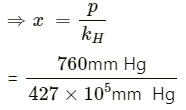
= 177.99 × 10−5
= 178 × 10−5 (approximately)
Hence, the mole fraction of methane in benzene is 178 × 10−5.
Q1.36: 100 g of liquid A (molar mass 140 g mol−1) was dissolved in 1000 g of liquid B (molar mass 180 g mol−1). The vapour pressure of pure liquid B was found to be 500 torr. Calculate the vapour pressure of pure liquid A and its vapour pressure in the solution if the total vapour pressure of the solution is 475 Torr.
Ans: Number of moles of liquid A, 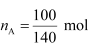
= 0.714 mol
Number of moles of liquid B, 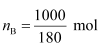
= 5.556 mol
Then, mole fraction of A,
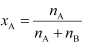
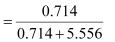
= 0.114
And, mole fraction of B, xB = 1 − 0.114
= 0.886
Vapour pressure of pure liquid B, pbo = 500 torr
Therefore, vapour pressure of liquid B in the solution,
pb = pboxb
= 500 × 0.886
= 443 torr
Total vapour pressure of the solution, ptotal = 475 torr
Vapour pressure of liquid A in the solution,
pA = ptotal − pB
= 475 − 443
= 32 torr
Now,
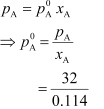
= 280.7 torr
Hence, the vapour pressure of pure liquid A is 280.7 torr.
Q1.37: Vapour pressure of pure acetone and chloroform at 328 K are 741.8 mm Hg and 632.8 mm Hg respectively. Assuming that they form ideal solution over the entire range of composition, plot ptotal’ pchloroform’ and pacetone as a function of xacetone. The experimental data observed for different compositions of mixture is. Ans: From the question, we have the following data
Ans: From the question, we have the following data
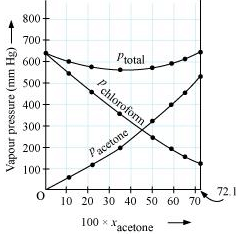 It can be observed from the graph that the plot for the ptotal of the solution curves downwards. Therefore, the solution shows negative deviation from the ideal behaviour.
It can be observed from the graph that the plot for the ptotal of the solution curves downwards. Therefore, the solution shows negative deviation from the ideal behaviour.
Q1.38: Benzene and toluene form ideal solution over the entire range of composition.The vapour pressure of pure benzene and naphthalene at 300 K are 50.71 mm Hg and 32.06 mm Hg respectively. Calculate the mole fraction of benzene in vapour phase if 80 g of benzene is mixed with 100 g of toluene.
Ans: Molar mass of benzene (C6H6) = 6 × 12 + 6 × 1 = 78 g mol-1
Molar mass of toluene (C6H5CH3) = 7 × 12 + 1 × 8 = 98 g mol-1
Now, no. of moles present in 80 g of benzene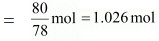
And, no. of moles present in 100 g of toluene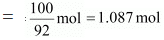
∴ Mole fraction of benzene,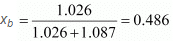
And, mole fraction of toluene, xt = 1 - 0.486 = 0.514
It is given that vapour pressure of pure benzene, P°b= 50.71 mm Hg
And, vapour pressure of pure toluene, P°t = 32.06 m Hg
Therefore, partial vapour pressure of benzene, pb = xb × p°t
= 0.486 × 50.71
= 24.645 mm Hg
Hence, mole fraction of benzene in vapour phase is given by:
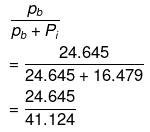
= 0.599
= 0.6
Q1.39: The air is a mixture of a number of gases. The major components are oxygen & nitrogen with approximate proportion of 20% is to 79% by volume at 298 K. The water is in equilibrium with air at a pressure of 10 atm. At 298 K if the Henry’s law constants for oxygen and nitrogen are 3.30 × 107 mm & 6.51 × 107 mm respectively, calculate the composition of these gases in water.
Ans: Percentage of oxygen (O2) in air = 20 %
Percentage of nitrogen (N2) in air = 79%
Also, it is given that water is in equilibrium with air at a total pressure of 10 atm,
that is, (10 × 760) mm Hg = 7600 mm Hg
Therefore,
Partial pressure of oxygen,

= 1520 mm Hg
Partial pressure of nitrogen,

= 6004 mmHg
Now, according to Henry’s law:
p = KH.x
For oxygen:
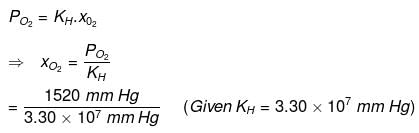
= 4.61 x 10-5
For nitrogen:
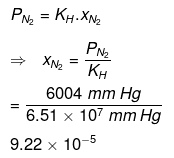
Hence, the mole fractions of oxygen and nitrogen in water are 4.61 × 10−5 and 9.22 × 10−5 respectively.
Q1.40: Determine the amount of CaCl2 (i = 2.47) dissolved in 2.5 litre of water such that its osmotic pressure is 0.75 atm at 27°C.
Ans: Structure of CaCl2We know that,
Structure of CaCl2We know that,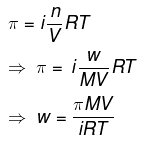
π = 0.75 atm
V = 2.5 L
i = 2.47
T = 300 K
Here,
R = 0.0821 L atm K-1mol-1
M = 1 × 40.2 × 35.5
= 111 g mol-1
Therefore,
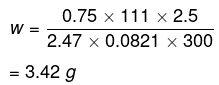
Hence, the required amount of CaCl2 is 3.42 g.
Q1.41: Determine the osmotic pressure of a solution prepared by dissolving 25 mg of K2SO4 in 2 liter of water at 25° C, assuming that it is completely dissociated.
Ans: When K2SO4 is dissolved in water, K+ and SO42- ions are produced.
K2SO4 → 2K+ + SO42-
Total number of ions produced = 3
i =3
Given,
w = 25 mg = 0.025 g
V = 2 L
T = 250C = (25 + 273) K = 298 K
Also, we know that:
R = 0.0821 L atm K-1mol-1
M = (2 × 39) (1 × 32) (4 × 16) = 174 g mol-1
Appling the following relation,
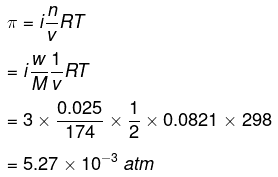
|
75 videos|349 docs|78 tests
|
FAQs on NCERT Solutions Class 12 Chemistry Chapter 1 - Solutions
| 1. What are the different types of solutions? |  |
| 2. How are solutions formed? |  |
| 3. What is solubility? |  |
| 4. How can the concentration of a solution be expressed? |  |
| 5. What is a saturated solution? |  |






















