NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism | Physics Class 12 PDF Download
2024
Q1: A tightly wound 100 turns coil of radius
(a) 44 mT
(b) 4.4 T
(c) 4.4 mT
(d) 44 T [2024]
Ans: (c)
The magnitude of magnetic field due to circular coil of N turns is given by
Q2: A sheet is placed on a horizontal surface in front of a strong magnetic pole. A force is needed to:
A. hold the sheet there if it is magnetic.
B. hold the sheet there if it is non-magnetic.
C. move the sheet away from the pole with uniform velocity if it is conducting.
D. move the sheet away from the pole with uniform velocity if it is both, non-conducting and non-polar.
Choose the correct statement(s) from the options given below:
(a) B and D only
(b) A and C only
(c) A, C and D only
(d) C only [2024]
Ans: (b)
To understand which statement(s) is/are correct, we must explore the interactions between the magnetic field and different types of materials (magnetic, non-magnetic, conducting, non-conducting)
Statement A: If a sheet is magnetic and placed near a strong magnetic pole, it will experience a magnetic force due to the magnetic field. This force could either attract or repel the sheet depending on the polarity of the magnetic pole and the induced or inherent poles in the sheet. A force is needed to hold the sheet stationary against this magnetic force. Hence, statement A is true
Statement B: If the sheet is non-magnetic, it will not experience any magnetic force because non-magnetic materials do not respond to magnetic fields in a manner where a force would be exerted on them. Thus, no external force is needed to hold a non-magnetic sheet in place near a magnetic pole. Statement B is false
Statement C: If the sheet is conducting and you move it away from the magnetic pole, it will experience a change in the magnetic flux through it. According to Faraday's Law of Electromagnetic Induction, a change in magnetic flux induces an electromotive force (EMF) and consequently, currents known as eddy currents in the conductor. These induced currents produce their own magnetic fields, which interact with the original magnetic field, leading to a force (Lenz's Law). To move the sheet away with uniform velocity, a force must counteract this magnetic interaction. Therefore, statement C is true
Statement D: If the sheet is non-conducting and non-polar, it will neither induce currents (since it's non-conducting) nor experience magnetic forces (since it's non-magnetic). Thus, moving such a sheet away from a magnetic pole with uniform velocity does not require overcoming any electromagnetic forces. Statement D is false
Given these explanations, the correct statements are A and C only
The correct choice is: Option B: A and C only.
2023
Q1: A long straight wire of length 2 m and mass 250 g is suspended horizontally in a uniform horizontal magnetic field of 0.7 T. The amount of current flowing through the wire will be (g = 9.8 ms-2)
(a) 2.45 A
(b) 2.25 A
(c) 2.75 A
(d) 1.75 A
Ans: (d)
Q2: A uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected in the region such that its velocity is pointed along the direction of fields, then the electron:
(a) will turn towards right of direction of motion
(b) will turn towards left of direction of motion
(c) speed will decrease
(d) speed will increase
Ans: (c)
Speed of electron will decrease due to electric force magnetic force of electron is zero.
Q3: A very long conducting wire is bent in a semi-circular shape from A to B as shown in the figure. The magnetic field at point P for steady current configuration is given by 
(a)
(b)
(c)
(d)
Ans: (c)
Pointed away from the page.
Q4: A wire carrying a current I along the positive x-axis has length L. It is kept in a magnetic field 
The magnitude of the magnetic force acting on the wire is
(a)3 lL
(b)√5 lL
(c)5 lL
(d)√3 lL
Ans: (c)
Magnetic force acting on a current-carrying wire is
2022
Q1: The shape of the magnetic field lines due to an infinite long, straight current carrying conductor is
(a) a plane
(b) a straight line
(c) circular
(d) elliptical
Ans: (c)
From the right hand curl rule, the shape of magnetic field lines due to long current carrying wire is circular (concentric circles)
Q2: Two very long, straight, parallel conductors A and B carry current of 5 A and 10 A respectively and are at a distance of 10 cm from each other. The direction of current in two conductors is same. The force acting per unit length between two conductors is : 
(a) 1 x 10-4 Nm-1 and is repulsive
(b) 2 x 10-4 Nm-1 and is attractive
(c) 2 x 10-4 Nm-1 and is repulsive
(d) 1 x 10-4 Nm-1 and is attractive
Ans: (d)
Q3: The magnetic field on the axis of a circular loop of radius 100 cm carrying current I = √2 A, at point 1 m away from the centre of the loop is given by :
(a) 6.28 x 10-4 T
(b) 3.14 x 10-7 T
(c) 6.28 x 10-7 T
(d) 3.14 x 10-4 T
Ans: (b)
Q4: A long solenoid of radius 1 mm has 100 turns per mm. If 1 A current flows in the solenoid, the magnetic field strength at the center of the solenoid is
(a)12.56 × 10–2 T
(b)12.56 × 10–4 T
(c)6.28 × 10–4 T
(d)6.28 × 10–2 T
Ans: (a)
We know, the magnetic field at the center of the solenoid
Q5: From Ampere’s circuital law for a long straight wire of circular cross-section carrying a steady current, the variation of the magnetic field in the inside and outside region of the wire is
(a)A linearly increasing function of distance up to the boundary of the wire and then linearly decreasing for the outside region.
(b)A linearly increasing function of distance r up to the boundary of the wire and then decreasing one with 1/r dependence for the outside region.
(c)A linearly decreasing function of distance up to the boundary of the wire and then a linearly increasing one for the outside region.
(d)Uniform and remains constant for both regions.
Ans: (b)
Q6: Given below are two statements
Statement I: Biot-Savart’s law gives us the expression for the magnetic field strength of an infinitesimal current element (Idl) of a current-carrying conductor only.
Statement II: Biot-Savart’s law is analogous to Coulomb’s inverse square law of charge q, with the former being related to the field produced by a scalar source, Idl while the latter being produced by a vector source, q. In light of the above statements choose the most appropriate answer from the options given below
(a)Both Statement I and Statement II are incorrect
(b)Statement I is correct and Statement II is incorrect
(c)Statement I is incorrect and Statement II is correct
(d)Both Statement I and Statement II are correct
Ans: (b)
According to Biot-Savart’s law
which applies to infinitesimal elements. It is analogous to Coulomb’s law, where IdI is the vector source and the electric field is produced by scalar source q. Here, statement I is correct and statement II is incorrect.
Q7: A square loop of side 1 m and resistance 1 Ω is placed in a magnetic field of 0.5 T. If the plane of loop is perpendicular to the direction of magnetic field, the magnetic flux through the loop is
(a) 2 weber
(b) 0.5 weber
(c) 1 weber
(d) Zero weber
Ans: (b)
2021
Q1: Two toroids 1 and 2 have total number of turns 200 and 100 respectively with average radii 40 cm and 20 cm respectively. If they carry same current i, the ratio of the magnetic fields along the two loops is
(a) 1 : 1
(b) 4 : 1
(c) 2 : 1
(d) 1 : 2
Ans: (a)
Q2: A thick current-carrying cable of radius 'R' carries current 'I' uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance 'r' from the axis of the cable is represented by:
A:
B:
C:
D:
Ans: (a)
Inside a current-carrying cylindrical conductor
Q3: An infinitely long straight conductor carries a current of 5 A as shown. An electron is moving with a speed of 105 m/s parallel to the conductor. The perpendicular distance between the electron and the conductor is 20 cm at an instant. Calculate the magnitude of the force experienced by the electron at that instant. 
(a)4π× 10–20 N
(b)8 × 10–20 N
(c)4 × 10–20 N
(d)8π× 10–20 N
Ans: (b)
f = 8 × 10–20 Newton.
Q4: Uniform conducting wire of length 12a and resistance 'R' is wound up as a current-carrying coil in the shape of,
(i) an equilateral triangle of side 'a'
(ii) a square of side 'a'
The magnetic dipole moments of the coil in each case respectively are:
(a)3Ia2 and 4Ia2
(b)4Ia2 and 3Ia2
(c)√3Ia2 and 3Ia2
(d)3Ia2 and Ia2
Ans: (c)
(no. of turns = 4)
M2 = a2I × 3 = 3Ia2
(no. of turns = 3)
Q9. In the product
What will be the complete expression for 
?
(a)
B:
(c)
(d)
Ans: (d)
Let the expression of B= Bii+Bjj+Bkk
Let's first find the cross-product of v and B.
We get three equations:
On solving the above equations we get,
Bi =-6
Bj =-6
Bk =-8
Thus the magnetic field vector is, B= -6i-6j-8k
2020
Q1: A spherical conductor of radius 10 cm has a charge of 3.2 × 10-7 C distributed uniformly. what is the magnitude of the electric field at a point 15 cm from the center of the sphere? 
Ans: (d)
Q2: A long solenoid of 50 cm in length having 100 turns carries a current of 2.5 A. The magnetic field at the center of the solenoid is : (μ0 = 4π × 10-7 Tm A-1)
(a)6.28×10-5 T
(b)3.14×10-5 T
(c)6.28×10-4 T
(d)3.14×10-4 T
Ans: (c)
The magnetic field for the solenoid is given by
B = μ0 nI
n = N/ℓ
= 4π × 10-7 × 200 × 2.5
= 4 × 3.14 × 10–7 × 500
= 2000 × 3.14 × 10–7
= 6.14 × 10–4 T
2019
Q1: A straight conductor carrying current i splits into two parts as shown in the figure. The radius of the circular loop is R. The total magnetic field at the centre P at the loop is
Ans: (a)
The magnetic field at the centre of an arc subtended at an angle θ is given by
Then, the magnetic field due to larger arc AB is
which acts in inward direction according to right hand thumb rule. And magnetic field due to smaller arc AB is
which acts in outward direction.
The resultant magnetic field
which acts in inward direction as B1> B2.
Two arcs can also be seen as the two resistances in parallel combination.
So, the potential across them will be same i.e.
From Eq. (iii) and (v), we get
Q2: A cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field. B with the distance d from the center of the conductor, is correctly represented by the figure :
A:
B:
C:
D:
Ans: (c)
Solution:
Inside (d < R) Magnetic field inside the conductor
or B = Kd ...(i)
A straight line passing through the origin
At surface (d = R)
...(ii)
Maximum at surface Outside (d > R)
Q3: Ionized hydrogen atoms and α-particles with the same momenta enter perpendicular to a constant magnetic field, B. The ratio of the radii of their paths rH : ra will be :
(a)2 : 1
(b)1 : 2
(c)4 : 1
(d)1 : 4
Ans: (a)
Solution:
Q4: Ionized hydrogen atoms and? a-particles with the same momenta enter perpendicular to a constant magnetic field, B. The ratio of the radii of their paths will be:
(a)2:1
(b)1:2
(c)4:1
(d)1:4
Ans: (a)
Q5: At point A on the earth's surface the angle of dip, δ = +25°. At a point B on the earth's surface the angle of dip, δ = −25°. We can interpret that:
(a)A and B are both located in the northern hemisphere.
(b)A is located in the southern hemisphere and B is located in the northern hemisphere.
(c)A is located in the northern hemisphere and B is located in the southern hemisphere.
(d)A and B are both located in the southern hemisphere.
Ans: (c)
The angle of dip is the angle between the earth's resultant magnetic field from the horizontal. The dip is zero at the equator and positive in the northern hemisphere.
In the southern hemisphere, the dip angle is considered negative.
Q6: A cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field. B with the distance d from the center of the conductor, is correctly represented by the figure :
(a)
(b)
(c) 
(d)
Ans: (c)
Inside (d < R)
The magnetic field inside the conductor
A straight line passing through the origin at the surface (d = R)
Maximum at surface
Outside (d > R)
2018
Q1: A metallic rod of mass per unit length 0.5 kgm-1 is lying horizontally on a smooth inclined plane which makes an angle of 30° with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of induction 0.25 T is acting on it in the vertical direction. The current flowing in the rod to keep it stationary is-
(a)14.76 A
(b)5.98 A
(c)7.14 A
(d)11.32 A
Ans: (d)
For Equilibrium,
mg sin 30° =1lBcos30°
2017
Q1: A 250-turn rectangular coil of length 2.1 cm and width 1.25 cm carries a current of 85 µA and is subjected to a magnetic field of strength 0.85 T. Work done for rotating the coil by 180º against the torque is:
(a)4.55 µJ
(b)2.3 µJ
(c)1.15 µJ
(d)9.1 µJ
Ans: (d)
Solution:
W = MB (cosθ1– cosθ2)
When it is rotated by an angle of 180º then
W = 2MB
W = 2 (NIA)B
= 2 x 250 x 85 x 10-6[1.25 x 2.1 x 10-4] x 85 x 10-2
= 9.1μJ
Q2: An arrangement of three parallel straight wires placed perpendicular to the plane of paper carrying the same current 'I' along the same direction is shown in Fig. The magnitude of force per unit length on the middle wire 'B' is given by:
A:
B:
C:
D:
Ans: (c)
Solution:
2016
Q1: A long straight wire of radius a carries a steady current I. The current is uniformly distributed over its cross-section. The ratio of the magnetic fields B and B ′ at radial distances a /2 and 2a respectively, from the axis of the wire is
(a) 1/2
(b) 1
(c) 4
(d) 1/4
Ans: (b)
Consider two amperian loops of radius a / 2 and 2a as shown in the diagram.Applying Ampere’s circuital law for these loops we get,
Similarly, for bigger amperian loop.
Q2: A long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. It is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
(a) nB
(b) n2B
(c) 2nB
(d) 2n2B
Ans: (b)
(For a circular coil) where, n : Number of turns in circular coil
Q3: A square loop ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be
(a) 
(b) 
(c) 
(d) 
Ans: (d)
Consider the given figure,
From the above figure, it can be seen that the direction of currents in a long straight conductor XY and arm AB of a square loop ABCD are in the same direction. So, there exist a force of attraction between the two, which will be experienced by FBA as
In the case of XY and arm CD, the direction of currents are in the opposite direction. So, there exist a force of repulsion which will be experienced by CD as
Therefore, net force on the loop ABCD will be
Q4: A long straight wire of radius a carries a steady current I. The current is uniformly distributed over its cross-section. The ratio of the magnetic fields B and B`, at radial distances a/2 and 2a respectively, from the axis of the wire is:
(a)4
(b)1/4
(c)1/2
(d)1
Ans: (d)
Solution:
Consider two amperian loops of radius a/2 and 2a as shown in the diagram.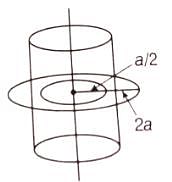
Applying Ampere's circuital law for these loops, we get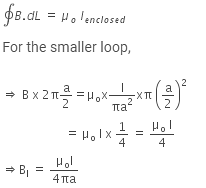
B1 acts at a distance a/2 from the axis of the wire.
Similarly, for a bigger amperian loop,
Total current enclosed by amperian loop 2.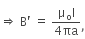
at a distance 2a from the axis of the wire.
2015
Q1: An electron moving in a circular orbit of radius r makes n rotations per second. The magnetic field produced at the centre has magnitude
(a) 
(b) Zero
(c) 
(d) 
Ans: (d)
As I = q/t. So, for an electron revolving in a circular orbit of radius r
q = e and t = T
The magnetic field produced at the centre is
Q2: An electron is moving in a circular path under the influence of a transverse magnetic field of 3. 57 × 10−2 T. If the value of e/m is 1.76 × 1011 C/kg, the frequency of revolution of the electron is
(a) 1 GHz
(b) 100 MHz
(c) 62.8 MHz
(d) 6.28 MHz
Ans: (a)
As we know that, radius of a charged particle in a magnetic field B is given by
where, r = charge on the particle
v = speed of the particle
∴The time taken to complete the circle,
2014
Q1: In an ammeter 0.2% of main current passes through the galvanometer. If resistance of galvanometer is G, the resistance of ammeter will be
(a) 1/499 G
(b) 499/500 G
(c) 1/500 G
(d) 500 / 499 G
Ans: (c)
For ammeter,
Equivalent resistance of ammeter,
Q2: Two identical long conducting wires AOB and COD are placed at a right angle to each other, with one above the other such that ‘O’ is their common point for two. The wires carry I1 and I2 currents, respectively. Point ‘P’ is lying at a distance ‘d’ from ‘O’ along a direction perpendicular to the plane containing the wires. The magnetic field at the point ‘P’ will be :
A:
B:
C:
D:
Ans: (b)
Solution:
The point P is lying at a distance d along the z-axis.
|
97 videos|336 docs|104 tests
|
FAQs on NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism - Physics Class 12
| 1. What is the relationship between moving charges and magnetism? |  |
| 2. How does the magnetic field around a moving charge differ from a stationary charge? | |
| 3. How does the force on a moving charge in a magnetic field change with the angle between the velocity and magnetic field? | |
| 4. What is the Lorentz force law and how does it relate to moving charges and magnetism? | |
| 5. How can the direction of the magnetic field around a current-carrying wire be determined using the right-hand rule? | |
|
1.9K Views |
|
4.92/5 Rating |
|
Dec 22, 2024 Last updated |
|
Explore Courses for NEET exam
|
|
shortcuts and tricks
,past year papers
,ppt
,study material
,Objective type Questions
,Semester Notes
,Exam
,Previous Year Questions with Solutions
,NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism | Physics Class 12
,mock tests for examination
,Summary
,NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism | Physics Class 12
,MCQs
,Important questions
,video lectures
,NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism | Physics Class 12
,Viva Questions
,Sample Paper
,Free
,practice quizzes
,Extra Questions
,
NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism Free PDF Download
Importance of NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism
NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism Notes
NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism NEET
Study NEET Previous Year Questions (2014-2024): Moving Charges & Magnetism on the App
|
© EduRev
|
Education Revolution
|
|
