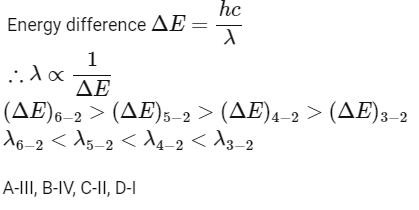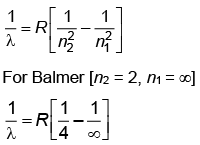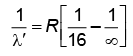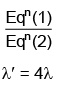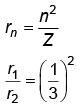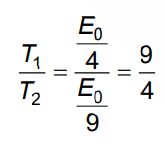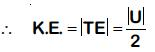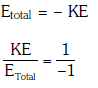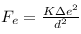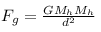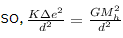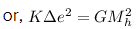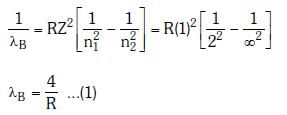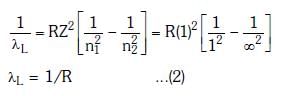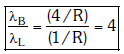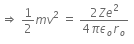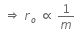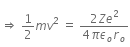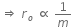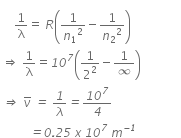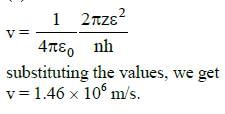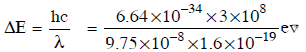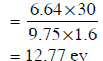NEET Previous Year Questions (2014-2025): Atoms | Physics Class 12 PDF Download
2025
Q1: A particle of mass m is moving around the origin with a constant force F pulling it towards the origin. If Bohr model is used to describe its motion, the radius r of the nth orbit and the particle's speed v in the orbit depend on n as: (NEET 2025)
(a) 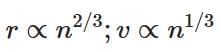
(b) 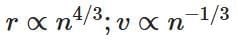
(c) 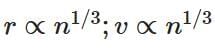
(d) 
Ans: (a)
Given, force is constant
F = mv2 / r
⇒ v2 / r = constant
⇒ r ∝ v2 ...(1)
L = mvr = nh / 2π ...(2)
On solving equation (1) and equation (2):
v ∝ n1/3 and r ∝ n2/3
2024
Q1: Given below are two statements: (NEET 2024)
Statement I: Atoms are electrically neutral as they contain equal number of positive and negative charges.
Statement II: Atoms of each element are stable and emit their characteristic spectrum.
In the light of the above statements, choose the most appropriate answer from the options given below.
(a) Both Statement I and Statement II are correct
(b) Both Statement I and Statement II are incorrect
(c) Statement I is correct but Statement II is incorrect
(d) Statement I is incorrect but Statement II is correct
Ans: (c) Statement I is correct but Statement II is incorrect
Let's analyze each statement one by one to determine the correctness:
- Statement I: "Atoms are electrically neutral as they contain equal number of positive and negative charges."
This statement is correct. Atoms are composed of protons, neutrons, and electrons. Protons have a positive charge, electrons have a negative charge, and neutrons have no charge. In a neutral atom, the number of protons (positive charges) equals the number of electrons (negative charges), thus making the atom electrically neutral. The positive and negative charges balance each other, resulting in no overall charge.- Statement II: "Atoms of each element are stable and emit their characteristic spectrum."
This statement requires modification for accuracy. Atoms emit their characteristic spectrum when they are excited and then return to a lower energy state. The emission of a spectrum is not linked directly to the stability of an atom; it is linked to the electronic transitions within the atom. The term "stable" in relation to atoms typically refers to the overall energy state of an atom being at its lowest or in a ground state. However, atoms can emit radiation whether they are in a stable ground state or in an excited state. Moreover, not all atoms are inherently stable; some may be radioactive and unstable. The part that atoms emit their characteristic spectrum under certain conditions (like excitation) is correct, but linking this property strictly to stability is misleading.Based on the analysis:
Statement I is correct.
Statement II is partially correct, as it is accurate that each element can emit a characteristic spectrum when excited, but incorrect in generalizing that all such atoms are stable.
Therefore, the correct option is:
Option C: Statement I is correct but Statement II is incorrect.
Q2: Match List I with List II: (NEET 2024)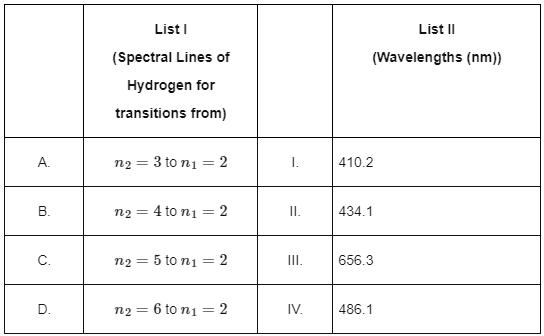 Choose the correct answer from the options given below:
Choose the correct answer from the options given below:
(a) A-II, B-I, C-IV, D-III
(b) A-III, B-IV, C-II, D-I
(c) A-IV, B-III, C-I, D-II
(d) A-I, B-II, C-III, D-IV [2024]
Ans: (b) A-III, B-IV, C-II, D-I
Q3: Match List-I (Spectral Series) with List-II (corresponding wave number expressions). (NEET 2024)
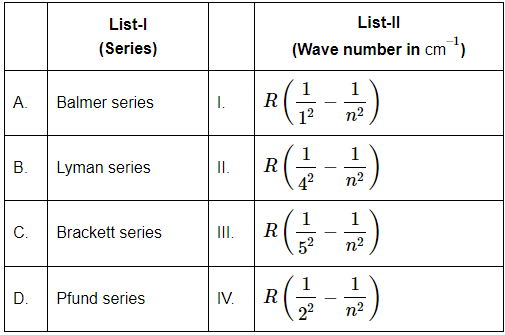
Choose the correct answer from the options given below:
(a) A-I, B-IV, C-III, D-II
(b) A-II, B-III, C-IV, D-I
(c) A-IV, B-I, C-II, D-III
(d) A-III, B-II, C-I, D-IV
Ans: (c)
Spectral Series and Corresponding Wave Number Expressions:
Lyman series (B):
The wave number expression for the Lyman series corresponds to transitions where the electron falls to the n=1 energy level.
The correct formula for this is: R (1 - 1/n²).
This corresponds to Option I in List-II.
Balmer series (A):
The Balmer series corresponds to transitions where the electron falls to the n=2 energy level.
The correct formula for this is: R (1/4 - 1/n²).
This corresponds to Option II in List-II.
Brackett series (C):
The Brackett series corresponds to transitions where the electron falls to the n=4 energy level.
The correct formula for this is: R (1/16 - 1/n²).
This corresponds to Option III in List-II.
Pfund series (D):
The Pfund series corresponds to transitions where the electron falls to the n=5 energy level.
The correct formula for this is: R (1/25 - 1/n²).
This corresponds to Option IV in List-II.
Matching the Options:
A: Balmer series → II. R (1/4 - 1/n²)
B: Lyman series → I. R (1 - 1/n²)
C: Brackett series → III. R (1/16 - 1/n²)
D: Pfund series → IV. R (1/25 - 1/n²)
Correct Answer: (c) A-IV, B-I, C-II, D-III
Q4:The spectral series which corresponds to the electronic transition from the levels n₂ = 5, 6, … to the level n₁ = 4 is: (NEET 2024)
(a) Pfund series
(b) Brackett series
(c) Lyman series
(d) Balmer series
Ans: (b)
The spectral series corresponds to electronic transitions where electrons move from higher energy levels (n₂) to a specific lower energy level (n₁). The series are defined as follows:
- Lyman series: n₁ = 1 (ultraviolet region).
- Balmer series: n₁ = 2 (visible region).
- Brackett series: n₁ = 4 (infrared region).
- Pfund series: n₁ = 5 (infrared region).
For the given transition from n₂ = 5, 6, … to n₁ = 4, the series is determined by the lower energy level n₁. Since n₁ = 4, this corresponds to the Brackett series.
The correct answer is (b) Brackett series.
Q5: Some energy levels of a molecule are shown in the figure with their wavelengths of transitions. (NEET 2024)
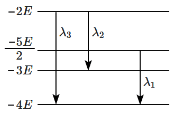
Then, choose the correct relation between the wavelengths:
(a) λ₃ > λ₂, λ₁ = 2λ₂
(b) λ₃ > λ₂, λ₁ = 4λ₂
(c) λ₁ > λ₂, λ₂ = 2λ₃
(d) λ₂ > λ₁, λ₂ = 2λ₃
Ans: (a)
Solution:
2023
Q.1. The minimum wavelength of X-rays produced by an electron accelerated through a potential difference of V volts is proportional to (NEET 2023)(a) √V
(b) 1/V
(c) 1/√V
(d) V2
Ans: (b) 1/V
Q.2. In hydrogen spectrum, the shortest wavelength in the Balmer series is λ. The shortest wavelength in the Bracket series is (NEET 2023)
(a) 2λ
(b) 4λ
(c) 9λ
(d) 16λ
Ans: (b) 4λ
λ = 4/R ...(1)
For Bracket, (n2 = 4, n1 = ∞)
λ' = 16/R ...(2)
Q.3. The radius of inner most orbit of hydrogen atom is 5.3 × 10 –11 m. What is the radius of third allowed orbit of hydrogen atom? (NEET 2023)
(a) 0.53 Å
(b) 1.06 Å
(c) 1.59 Å
(d) 4.77 Å
Ans: (d) 4.77 Å
r2 = 9r1 = 5.3 x 10-11 x 9
= 47.7 × 10–11
= 4.77 Å
Q4: The ground state energy of a hydrogen atom is −13.6eV. The energy needed to ionize the hydrogen atom from its second excited state will be: (NEET 2023)
(a) 13.6eV
(b) 6.8eV
(c) 1.51eV
(d) 3.4eV
Ans: (c)
Key Concept:
The ground state energy of a hydrogen atom is -13.6 eV.
The energy levels of a hydrogen atom are given by the formula:
En = -13.6 eV / n²
where n is the principal quantum number.
Steps:
Energy of the second excited state (n = 3): The second excited state corresponds to n = 3. Using the formula for energy levels:
E3 = -13.6 eV / (3)² = -13.6 eV / 9 = -1.51 eV
Energy required to ionize the atom: To ionize the atom, we need to take the atom from its second excited state (n = 3) to the continuum, where the energy is 0 eV (since ionization means the electron is completely removed from the atom).
The energy required to ionize is the difference between the energy of the second excited state and the energy at infinity (ionized state, 0 eV):
Energy required = 0 eV - (-1.51 eV) = 1.51 eV
Correct Answer: (c) 1.51 eV.
Q5: The wavelength of the Lyman series of the hydrogen atom appears in the: (NEET 2023)
(a) visible region
(b) far infrared region
(c) ultraviolet region
(d) infrared region
Ans: (c)
The Lyman series of the hydrogen atom corresponds to electronic transitions where the electron falls to the n = 1 energy level from higher energy levels (n = 2, 3, 4, ...).
The wavelengths of light emitted during these transitions lie in the ultraviolet (UV) region of the electromagnetic spectrum. This is because the energy difference between the levels involved in the Lyman series is large, resulting in higher energy photons, which correspond to shorter wavelengths.
Correct Answer: (c) ultraviolet region.
Q6: The angular momentum of an electron moving in an orbit of a hydrogen atom is 1.5(h/π). The energy in the same orbit is nearly: (NEET 2023)
(a) -1.5 eV
(b) -1.6 eV
(c) -1.3 eV
(d) -1.4 eV
Ans: (a)
Angular momentum equation:
The angular momentum of an electron in a hydrogen atom orbit is given by the quantum mechanical condition:
L = nh / 2πWhere:
- L is the angular momentum,
- n is the principal quantum number,
- h is Planck's constant.
Given that the angular momentum is 1.5 h / π, we can equate it to the above formula:
1.5 h / π = nh / 2π
Simplifying by canceling h (assuming h ≠ 0):
1.5 / π = n / 2π
Multiplying both sides by π:
1.5 = n / 2Solving for n:
n = 1.5 × 2 = 3
So, the principal quantum number n = 3.Energy Calculation:
The energy of an electron in a hydrogen atom is given by:
En = -13.6 eV / n²For n = 3:
E3 = -13.6 eV / 3² = -13.6 eV / 9 ≈ -1.511 eV
The value -1.511 eV is closest to -1.5 eV among the given options.
Conclusion: The correct answer is (a) -1.5 eV.
2022
Q.4. Let T1 and T2 be the energy of an electron in the first and second excited states of hydrogen atoms, respectively. According to Bohr’s model of an atom, the ratio T1 : T2 is (2022)
(a) 4 : 1
(b) 4 : 9
(c) 9 : 4
(d) 1 : 4
Ans: (c) 9 : 4
En = Eo / n2
For first excited state: n = 2
For second excited state n = 3
2020
Q.5. For which one of the following, Bohr model is not valid? (2020)
(a) Deuteron atom
(b) Singly ionised neon atom (Ne+)
(c) Hydrogen atom
(d) Singly ionised helium atom (He+)
Ans: (b) Singly ionised neon atom (Ne+)
Bohr Model is valid only for those atoms which have one electron in orbit.
Bohr Model
2019
Q.6. The total energy of an electron in an atom in an orbit is –3.4 eV. Its kinetic and potential energies are, respectively: (2019)
(a) –3.4 eV, –3.4 eV
(b) –3.4 eV, –6.8 eV
(c) 3.4 eV, –6.8 eV
(d) 3.4 eV, 3.4 eV
Ans: (c) 3.4 eV, –6.8 eV
In Bohr's model of H atom
∴ K.E. = 3.4 eV
U = –6.8 eV
Q.7. α-particle consists of : (2019)
(a) 2 protons and 2 neutrons only
(b) 2 electrons, 2 protons and 2 neutrons
(c) 2 electrons and 4 protons only
(d) 2 protons only
Ans: (a) 2 protons and 2 neutrons only
α-particle is nucleus of Helium which has two protons and two neutrons.
2018
Q.8. The ratio of kinetic energy to the total energy of an electron in a Bohr orbit of the hydrogen atom,is :- (2018)
(a) 1 : 1
(b) 1 : –1
(c) 2 : –1
(d) 1 : –2
Ans: (b) 1 : –1
2017
Q.9. Suppose the charge of a proton and an electron differ slightly. One of them is – e, the other is(e + De). If the net of electrostatic force and gravitational force between two hydrogen atoms placed at a distance d (much greater than atomic size) apart is zero, then De is of the order of [Given mass of hydrogen mh = 1.67 × 10–27 kg] (2017)
(a) 10–23 C
(b) 10–37 C
(c) 10–47 C
(d) 10–20 C
Ans: (b) 10–37 C
We know, a hydrogen atom has one electron and one proton
so, net charge on each hydrogen atom = (e + ∆e - e) = ∆e
so, electrostatic force ,
gravitational force,
where Mh denotes mass of hydrogen
a/c to question,
gravitational force = electrostatic force
we know, K = 9 × 109 Nm²/C², G = 6.67 × 10-11 Nm²/Kg² , Mh = 1.67 × 10-27 Kg
so, 9 × 109 × ∆e² = 6.67 × 10-11 × (1.67 × 10-27)²
or, ∆e² = 6.67 × 10-11 × 1.67 × 1.67 × 10-54/9 × 109
or, ∆e = 1.43767 × 10-37 C
Q.10. The ratio of wavelengths of the last line of Balmer series and the last line of Lyman series is :- (2017)
(a) 1
(b) 4
(c) 0.5
(d) 2
Ans: (b) 4
For last line of Balmer : n1 = 2 & n2 = ∞
For last line Lyman series : n1 = 1 & n2 = ∞
2016
Q.11. When an α-particle of mass 'm' moving with velocity 'v' bombards on a heavy nucleus of charge 'Ze' its distance of closet approach from the nucleus depends on m as : (2016)
(a) m
(b) 1/m
(c) 1/√m
(d) 1/m2
Ans: (b) 1/m
When an alpha particle moving with velocity v bombards on a heavy nucleus of charge Ze, then there will be no loss of energy.
Initial Kinetic energy of the alpha particle = Potential energy of alpha particle at closest approach.
That is,
This is the required distance of closest approach to alpha particle from the nucleus.
When an alpha particle moving with velocity v bombards on a heavy nucleus of charge Ze, then there will be no loss of energy.
Initial Kinetic energy of the alpha particle = Potential energy of alpha particle at closest approach.
That is,
This is the required distance of closest approach to alpha particle from the nucleus.
Q.12. Given the value of Rydberg constant is 107 m-1, the wave number of the last line of the Balmer series in hydrogen spectrum will be : (2016)
(a) 2.5 x 107m-1
(b) 0.025 x 104m-1
(c) 0.5 x 107m-1
(d) 0.25 x 107m-1
Ans: (d) 0.25 x 107m-1
Rydberg constant, r = 107 m-1
For last line in Balmer series,
n2 = ∞; n1 = 2
We know,
2015
Q.13. Consider 3rd orbit of He+ (Helium), using non-relativistic approach, the speed of electron in this orbit will be [given K = 9 x 109 constant, Z = 2 and h(Planck's Constant) = 6.6 x 10-34 J s] (2015)
(a) 3.0 x 108 m/s
(b) 2.92 x 106 m/s
(c) 1.46 x 106 m/s
(d) 0.73 x 106 m/s
Ans: (c) 1.46 x 106 m/s
Q.14. If radius of the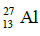 nucleus is taken to be RAl, then the radius of
nucleus is taken to be RAl, then the radius of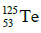 nucleus is nearly : (2015)
nucleus is nearly : (2015)
(a) 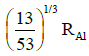
(b)
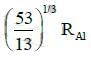
(c)

(d)
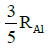
Ans: (c) 5 / 3 RAI
Radius of the nucleus goes as R ∝ A1/3, where A is the atomic mass. If RTe is the radius of the nucleus of telurium atom and RAl is the radius of the nucleus of aluminium atom we have
2014
(a) 6
(b) 10
(c) 3
(d) 2
Ans: (a) 6
There is no Question for NEET 2021
|
88 videos|421 docs|88 tests
|
FAQs on NEET Previous Year Questions (2014-2025): Atoms - Physics Class 12
| 1. What is an atom? |  |
| 2. How many electrons can each shell of an atom hold? |  |
| 3. What is the atomic number of an element? |  |
| 4. What is an isotope? |  |
| 5. How do electrons move in different energy levels around the nucleus of an atom? |  |