NEET Previous Year Questions (2014-2024): Ray Optics & Optical Instruments | Physics Class 12 PDF Download
2024
Q1: A light ray enters through a right angled prism at point P with the angle of incidence 30∘ as shown in figure. It travels through the prism parallel to its base BC and emerges along the face AC. The refractive index of the prism is: (a) √5/4
(a) √5/4
(b) √5/2
(c) √3 /4
(d) √3/2 [2024]
Ans: (b)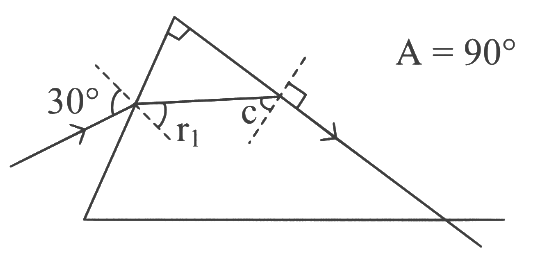 In prism, r1 + c = A
In prism, r1 + c = A
Apply Snell's law, on incidence surface
On squaring, 

Q2: A small telescope has an objective of focal length 140cm and an eye piece of focal length 5.0cm. The magnifying power of telescope for viewing a distant object is:
(a) 34
(b) 28
(c) 17
(d) 32 [2024]
Ans: (b)
The magnifying power of a telescope when viewing distant objects can be calculated using the formula:
Given in the problem:
Focal Length of Objective Lens, f0 = 140cm
Focal Length of Eyepiece Lens,
Substituting these values into the formula gives:
Thus, the magnifying power of the telescope is 28. The correct answer is Option B.
2023
Q1: Light travels a distance x in time t1 in air and 10x in time t2 in another denser medium. What is the critical angle for this medium?
(a) 
(b) 
(c) 
(d) 
Ans: (d)
Q2: Two thin lenses are of the same focal lengths (f), but one is convex and the other one is concave. When they are placed in contact with each other, the equivalent focal length of the combination will be
(a) Zero
(b) f/4
(c) f/2
(d) Infinite
Ans: (d)
Convex lens f1 > 0, concave lens f2 < 0
Q3: In the figure shown here, what is the equivalent focal length of the combination of lenses (Assuming that all layers are thin)?  (a)40 cm
(a)40 cm
(b) –40 cm
(c) –100 cm
(d) –50 cm
Ans: (c)

Q4: A lens is made up of 3 different transparent media as shown in figure. ! point object O is placed on its axis beyond 2f. How many real images will be obtained on the other side?

(a) 2
(b) 1
(c) No image will be formed
(d) 3
Ans: (d)
Since lens is made of three materials so three μ and hence three images.
Q5: εo and μo are the electric permittivity and magnetic permeability of free space respectively. If the corresponding quantities of a medium are 2 εo and 1.5 μo respectively, the refractive index of the medium will nearly be :
(a) √2
(b) √3
(c) 3
(d) 2
Ans: (b)
The refractive index n of a medium is related to the electric permittivity (ϵ) and magnetic permeability (μ) of the medium as follows:
Given:
- The electric permittivity of the medium is ϵ=2ϵ0,
- The magnetic permeability of the medium is μ=1.5μ0.
Substitute these values into the equation:
Simpifying, 
Q6: A horizontal ray of light is incident on the right-angled prism with prism angle 6∘. If the refractive index of the material of the prism is 1.5, then the angle of emergence will be:

(a) 9o
(b) 10o
(c) 4o
(d) 6o
Ans: (a)

Q7: Which set of colors will come out in air for a situation shown in figure?
 (a) Yellow, Orange and Red
(a) Yellow, Orange and Red
(b) All
(c) Orange, Red and Violet
(d) Blue, Green and Yellow
Ans: (a)

Q8: An object is mounted on a wall. Its image of equal size is to be obtained on a parallel wall with the help of a convex lens placed between these walls. The lens is kept at distance x in front of the second wall. The required focal length of the lens will be:
(a) less than x/4
(b) more than x/44 but less than x/2
(c) x/2
(d) x/4
Ans: (c)

When of an equal size image is formed the
magnifi cation is unity.
i.e., v = u
image distance = object distance
Here, v = x
but according to lens formula,
1/u + 1/v = 1/f
2/v = 1/f
f =v/2 = x/2 = focal length of the lens is x/2.
Q9: For Young's double slit experiment, two statements are given below :
Statement I : If screen is moved away from the plane of slits, angular separation of the fringes remains constant.
Statement II : If the monochromatic source is replaced by another monochromatic source of larger wavelength, the angular separation of fringes decreases.
In the light of the above statements, choose the correct answer from the options given below :
(a) Both Statement I and Statement II are false
(b) Statement I is true but Statement II is false
(c) Statement I is false but Statement II is true
(d) Both Statement I and Statement II are true
Ans: (b)
In Young's double slit experiment, the angular separation of the fringes (θ) is given by :

where m is the fringe order, λ is the wavelength of the light, and d is the distance between the slits.
Now, let's analyze both statements: Statement I: If the screen is moved away from the plane of the slits, the angular separation of the fringes remains constant.
This statement is true because the angular separation of the fringes (θ) does not depend on the distance between the screen and the slits. It only depends on the fringe order (m), the wavelength of the light (λ), and the distance between the slits (d).
Statement II: If the monochromatic source is replaced by another monochromatic source of larger wavelength, the angular separation of fringes decreases.
This statement is false because if the wavelength (λ) increases, the angular separation of the fringes (θ) also increases according to the formula :

So, the correct answer is : Option (b) Statement I is true but Statement II is false.
2022
Q1: During a cloudy day, a primary and a secondary rainbow may be created, then the :
(a) secondary rainbow is due to single internal reflection and is formed above the primary one.
(b) primary rainbow is due to double internal reflection and is formed above the secondary one.
(c) primary rainbow is due to double internal reflection and is formed below the secondary one.
(d) secondary rainbow is due to double internal reflection and is formed above the primary one.
Ans: (d)
Primary rainbow is result of three-step process, that is, refraction, internal reflection and refraction.
Secondary rainbow is result of four step process, that is, refraction, internal reflection, internal reflection and refraction.
Secondary rainbow appears above the primary rainbow.
Q2: If the screen is moved away from the plane of the slits in a Young's double slit experiment, then the :
(a) linear separation of the fringes decreases
(b) angular separation of the fringes increases
(c) angular separation of the fringes decreases
(d) linear separation of the fringes increase
Ans: (d)
In YDSE,
Separation between fringes is
Related to fringed width 
If D is increased ft increases while
Angular separation is independent of distance between slits and screen (D)
As angular separation = 
Q3: After passing through a polariser a linearly polarised light of intensity I is incident on an analyser making an angle of 30∘ with that of the polariser. The intensity of light emitted from the analyser will be
(a) 2I / 3
(b) I/ 2
(c) I / 3
(d) 3I / 4
Ans: (d)
According to the Malu's Law

Q4: An astronomical refracting telescope is being used by an observer to observe planets in normal adjustment. The focal lengths of the objective and eye piece used in the construction of the telescope are 20 m and 2 cm respectively. Consider the following statements about the telescope :
(a) The distance between the objective and eye piece is 20.02 m
(b) The magnification of the telescope is (−) 1000
(c) The image of the planet is erect and diminished
(d) The aperture of eye piece is smaller than that of objective
The correct statements are :
(a) (a), (b) and (d)
(b) (a), (b) and (c)
(c) (b), (c) and (d)
(d) (c) , (d) and (a)
Ans: (a)
Given fo = 20 m = 2000 cm, fe = 2 cm
Distance between objective and eye piece I = f0 + fe
= 20 m + 2 cm = 20.02 cm
Magnification of telescope

Image formed by telescope is inverted.
Aperture of eye piece is smaller than that of objective.
So, statements (a), (b) and (c) are correct.
Q5: In a Young's double slit experiment, a student observes 8 fringes in a certain segment of screen when a monochromatic light of 600 nm wavelength is used. If the wavelength of light is changed to 400 nm, then the number of fringes he would observe in the same region of the screen is
(a) 6
(b) 8
(c) 9
(d) 12
Ans: (d)
Q6: When light propagates through a material medium of relative permittivity εr and relative permeability μr, the velocity of light, v is given by (c-velocity of light in vacuum)
(a) v = c
(b) 
(c) 
(d) 
Ans: (d)
The speed of light in a vacuum is denoted as c, which is approximately 3×108 m/s. When light travels through a medium, its speed is affected by the medium's properties, specifically its permittivity and permeability.
The speed of light v in a medium can be expressed using the formula:
where:
- c is the speed of light in vacuum,
- μr is the relative permeability of the medium,
- ϵr is the relative permittivity of the medium.
If we know the values of μr and ϵr, we can substitute them into the formula to calculate v.
The final expression for the speed of light in a medium with given relative permittivity and permeability is:
Q7: Two transparent media A and B are separated by a plane boundary. The speed of light in those media are 1.5 × 108 m/s and 2.0 × 108 m/s, respectively. The critical angle for a ray of light for these two media is
(a) sin–1 (0.750)
(b) tan–1 (0.500)
(c) tan–1 (0.750)
(d) sin–1 (0.500)
Ans: (a)
For TIR, ray of light should travel from denser to rarer medium

Q8: A biconvex lens has radii of curvature, 20 cm each. If the refractive index of the material of the lens is 1.5, the power of the lens is
(a) +20 D
(b) +5 D
(c) Infinity
(d) +2 D
Ans: (b)
Q9: A light ray falls on a glass surface of refractive index √3, at an angle 60°. The angle between the refracted and reflected rays would be
(a) 60°
(b) 90°
(c) 120°
(d) 30°
Ans: (b)
Given i = 60° and μ= √3
Here, angle of incidence i = tan–1 (μ)
Hence, reflected and refracted rays would be perpendicular to each other
2021
Q1: A lens of large focal length and large aperture is best suited as an objective of an astronomical telescope, since [NEET 2021]
(a) a large aperture contributes to the quality and visibility of the images
(b) a large area of the objective ensures better light gathering power
(c) a large aperture provides a better resolution
(d) All of the above
Ans: (d)
The objective of an astronomical telescope has large focal length and large aperture. Because the lens used is convex lens and the magnification of an astronomical telescope is directly proportional to the focal length of the objective lens.
This large aperture also contributes to the better quality and visibility of the images. Thus, it provides better resolution.
Due to large focal length of the objective, it covers large area which ensures better light gathering power.
Thus, all options (a), (b) and (c) are correct.
Q2: A convex lens A with a focal length of 20 cm and a concave lens B with a focal length of 5 cm are kept along the same axis with the distance d between them. If a parallel beam of light falling on A leaves B as a parallel beam, then distance d in cm will be
(a) 25
(b) 15
(c) 30
(d) 50
Ans: (b)
In the absence of a concave lens, the parallel beam will be focussed at F2 i.e. at a distance of 20 cm. from lens A.
The focal length of the concave lens is 5 cm. i.e. if this lens is placed at 5 cm from F2, then the beam will become parallel. So d = 15 cm.
Q3: Find the value of the angle of emergence from the prism. The refractive index of the glass is √3. 
(a) 45°
(b) 90°
(c) 60°
(d) 30°
Ans: (c) r1 + r2 = A = 30°
r1 + r2 = A = 30°
r2 = 30° (r1 = 0°)
From Snell's law,
√3sinr2 = 1 x sine
√3sin30° = sine
e = 60°
Q4: A lens of large focal length and large aperture is best suited as an objective of an astronomical telescope since:
(a) a large aperture contributes to the quality and visibility of the images.
(b) a large area of the objective ensures better light-gathering power.
(c) a large aperture provides a better resolution.
(d) all of the above.
Ans: (d)
The large aperture(a) of the objective lens provides a better resolution
∴ A good quality image is formed and also it gathers more light.
Q5: A point object is placed at a distance of 60 cm from a convex lens of focal length 30 cm. If a plane mirror were put perpendicular to the principal axis of the lens and at a distance of 40 cm from it, the final image would be formed at a distance of: 
(a) 30 cm from the plane mirror, it would be a virtual image.
(b) 20 cm from the plane mirror, it would be a virtual image.
(c) 20 cm from the lens, it would be a real image.
(d) 30 cm from the lens, it would be a real image.
Ans: (b)
first, for image formation from the lens
u = – 60 cm
f = + 30 cm
⇒ 
this real image formed by the lens acts as a virtual object for the mirror
A real image from the plane mirror is formed 20 cm in front of the mirror, hence at a 20 cm distance from the lens.
Now, for second refraction from lens,u = – 20 cm
f = +30 cm
So, the Final virtual image is 60 cm from the lens or 20 cm behind the mirror.
2020
Q1: An object is placed on the principal axis of a concave mirror at a distance of 1.5 f (f is the focal length). The image will be at
(a) −3f
(b) 1.5 f
(c) −1.5 f
(d) 3f
Ans: (a)
Object distance, u = − 1.5f
By mirror formula,

Q2: If the critical angle for total internal reflection from a medium to vacuum is 45°, then velocity of light in the medium is
(a) 1.5 × 108 m/s
(b) 3/√2× 108 m/s
(c) √2 × 108 m/s
(d) 3 × 108 m/s
Ans: (b)

Q3: A plano-convex lens of unknown material and unknown focal length is given. With the help of a spherometer we can measure the
(a) focal length of the lens
(b) radius of curvature of the curved surface
(c) aperture of the lens
(d) refractive index of the material
Ans: (b)
Spherometer is used to measure the radius of curvature of an item such as a lens and curved mirrors that are spherical in shape.
Q4: The power of a biconvex lens is 10 D and the radius of curvature of each surface is 10 cm. Then, the refractive index of the material of the lens is
(a) 4/3
(b) 9/8
(c) 5/3
(d) 3/2
Ans: (d)
Power of biconvex lens, P = 10D

Q5: A ray is an incident at an angle of incidence i on one surface of a small angle prism (with the angle of prism A) and emerges normally from the opposite surface. If the refractive index of the material of the prism is m, then the angle of incidence is nearly equal to:
(a) μA
(b) μA/2
(c) A/2μ
(d) 2A/μ
Ans: (a)
Light ray emerges from another surface normally, hence e(angle of emergence) = 0

Q6: Light with an average flux of 20 W/cm2 falls on a non-reflecting surface at normal incidence having a surface area of 20 cm2. The energy received by the surface during time span of 1 minute is:
(a) 24 × 103 J
(b) 48 × 103 J
(c) 10 × 103 J
(d) 12 × 103 J
Ans: (a)

= 400 w
∴ in 1 minute = 400 × 60
= 24000
2019
Q1: An equi-convex lens has power P it is cut into two symmetrical halves by a plane containing the principal axis. The power of one part will be (a) 0
(b) P/2
(c) P/4
(d) P
Ans: (d)
When the lens is cut along its principal axis, the focal length of the two halves will remain same because the radius of curvature of both the surfaces are still same. So, the power also remains same as

Q2: A double convex lens has focal length 25 cm. The radius of curvature of one of the surfaces is doubled of the other. Find the radii, if the refractive index of the material of the lens is 1.5.
(a) 100 cm, 50 cm
(b) 25 cm, 50 cm
(c) 18.75 cm, 37.5 cm
(d) 50 cm, 100 cm
Ans: (c)

Q3: Which colour of the light has the longest wavelength?
(a) Blue
(b) Green
(c) Violet
(d) Red
Ans: (d)
Different colours of white light have different wavelengths.
The descending order of the wavelength of the component of white light is

Q4: Pick the wrong answer in the context of the rainbow.
(a) When the light rays undergo two internal reflections in a water drop, a secondary rainbow is formed
(b) The order of colors is reversed in the secondary rainbow
(c) An observer can see a rainbow when his front is towards the sun
(d) Rainbow is a combined effect of dispersion refraction and reflection of sunlight
Ans: (c)
Solution:
Rainbows can't be observed when the observer faces toward the sun.
Q5: Two similar thin equi-convex lenses, of focal length f each, are kept coaxially in contact with each other such that the focal length of the combination is F1. When the space between the two lenses is filled with glycerine (which has the same refractive index (μ = 1.5) as that of glass) then the equivalent focal length is F2. The ratio F1 : F2 will be :
(a) 2 : 1
(b) 1 : 2
(c) 2 : 3
(d) 3 : 4
Ans: (b)
Solution:


Equivalent focal length in air 
When glycerin is filled inside, the glycerin lens behaves like a diverging lens of focal length (-f)

Q6: In total internal reflection when the angle of incidence is equal to the critical angle for the pair of media in contact, what will be the angle of refraction?
(a) 180°
(b) 0°
(c) Equal to the angle of incidence
(d) 90°
Ans: (d)
Solution:
At i = ic, the refracted ray grazes with the surface. So the angle of refraction is 90°.
So the angle of refraction is 90°.
2018
Q1: The refractive index of the material of a prism is √2 and the angle of the prism is 30°. One of the two refracting surfaces of the prism is made a mirror inwards, by silver coating. A beam of monochromatic light entering the prism from the other face will retrace its path (after reflection from the silvered surface) if its angle of incidence on the prism is:
(a) 60°
(b) 45°
(c) 30°
(d) zero
Ans: (b)
Solution:

Q2: An object is placed at a distance of 40 cm from a concave mirror of a focal length of 15 cm. If the object is displaced through a distance of 20 cm towards the mirror, the displacement of the image will be:
(a) 30 cm away from the mirror
(b) 36 cm away from the mirror
(c) 30 cm towards the mirror
(d) 36 cm towards the mirror
Ans:(b)
Solution:

Q3: An astronomical refracting telescope will have large angular magnification and high angular resolution, when it has an objective lens of:
(a) small focal length and large diameter
(b) large focal length and small diameter
(c) large focal length and large diameter
(d) small focal length and small diameter
Ans: (c)
Solution:
For astronomical refracting telescope
Angular magnification is for large focal length

2017
Q1: A beam of light from a source L is incident normally on a plane mirror fixed at a certain distance x from the source. The beam is reflected as a spot on a scale placed just above the source I. When the mirror is rotated through a small angle q, the spot of the light is found to move through a distance on the scale. The angle q is given by:
(a) y/x
(b) x/2y
(c) x/y
(d) y/2x
Ans: (d)
Solution:

Q2: The ratio of resolving powers of an optical microscope for two wavelengths λ1 = 4000 Å and λ2 = 6000 Å is :
(a) 9 : 4
(b) 3 : 2
(c) 16 : 81
(d) 8 : 27
Ans: (b)
Solution:

Q3: A thin prism having a refracting angle of 10° is made of glass with a refractive index of 1.42. This prism is combined with another thin prism of glass with a refractive index of 1.7. This combination produces dispersion without deviation. The refracting angle of the second prism should be:
(a) 6°
(b) 8°
(c) 10°
(d) 4°
Ans: (a)
Solution:
Dispersion without deviation this means that ray which is entering and the ray which is going out both are parallel,
As given,
A1=refracting angle of first prism=10o,
μ1=1.42, μ2=1.7
A2=refracting angle of second prism
As, δ=(μ−1)A
So, δTotal = δ1− δ2=0
where δ is the daviation and in this case total deviation is zero.
δ1=δ2
A2(μ2−1)=A1(μ1−1)
A2(0.7)=10(0.42)
A2=60
2016
Q1: The angle of incidence for a ray of light at a refracting surface of a prism is 45°. The angle of prism is 60°. If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are
(a) 30°; √2
(b) 45°; √2
(c) 30°; 1/√2
(d) 45°; 1/√2
Ans: (a)
Consider a ray of light PQ incident an the surface AB and moves along RS, after passing through the prism ABC.
It is given that the incident ray suffers minimum deviation. Therefore, the ray inside the prism must be parallel to the base BC of the prism.

From the geometry of the prism and the ray diagram, it is clear that
angle of incidence, i = 45°
angle of refraction r = r ′ = 30 °
angle of emergence, e = 45°
Therefore, minimum deviation suffered by the ray is


Q2: An air bubble in a glass slab with refractive index 1.5 (near normal incidence) is 5 cm deep when viewed from one surface and 3 cm deep when viewed from the opposite face. The thickness (in cm) of the slab is
(a) 8
(b) 10
(c) 12
(d) 16
Ans: (c)
Let thickness of the given slab is t.
According to the question, when viewed from both the surfaces


Q3: A beam of light consisting of red, green and blue colours is incident on a right angled prism. The refractive index of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively.

The prism will
(a) separate the blue colour part from the red and green colours
(b) separate all the three colours from one another
(c) not separate the three colours at all
(d) separate the red colour part from the green and blue colours
Ans: (d)
For refractive index of a index,



Thus, only red colour do not suffer total internal reflection.
Q4: The angle of a prism is A. One of its refracting surfaces is silvered. Light rays falling at an angle of incidence 2A on the first surface returns back through the same path after suffering reflection at the silvered surface. The refractive index µ , of the prism is
(a) 2 sin A
(b) 2 cos A
(c) 1/2cos A
(d) tan A
Ans: (b)
According to question, diagram is shown below.


Q5: Two identical glass (µg) = 3/2 equi-convex lenses of focal length f each are kept in contact. The space between the two lenses is filled with water ( µw ) = 4 3 The focal length of the combination is
(a) f/3
(b) f
(c) 4f/3
(d) 3f/4
Ans: (d)
Consider the situation shown is figure.Let radius of curvature of lens surfaces is R. The combination is equivalent to three lenses in contact.



Q6: A astronomical telescope has objective and eyepiece of focal lengths 40 cm 4 cm respectively.
To view an object 200 cm away from the objective, the lenses must be separated by a distance
(a) 46.0 cm
(b) 50.0 cm
(c) 54.0 cm
(d) 37.3 cm
Ans: (c)
According to question, Focal length of objective lens (F0 ) = + 40 cm
Focal length of eyepiece lens (Fe) = 4 cm
Object distance for objective lens (u0)= − 200 cm
Applying lens formula for objective lens


Image will be form at first focus of eyepiece lens.
So, for normal adjustment distance between objectives and eye piece lense (length of tube) will be
v + Fe ⇒ 50 + 4 ⇒ 54 cm
Q7: An astronomical telescope has an objective and eyepiece of focal lengths of 40 cm and 4 cm respectively. To view an object 200 cm away from the objective, the lenses must be separated by a distance :
(a) 54 cm
(b) 37.3 cm
(c) 46 cm
(d) 50 cm
Ans: (a)
Solution:
According to a question,
The focal length of the objective lens, Fo = +40 cm
The focal length of the eyepiece, Fe = 4 cm
Object distance for the objective lens (uo) = -200 cm
Applying lens formula for the objective lens,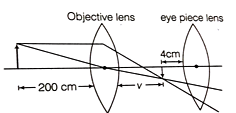
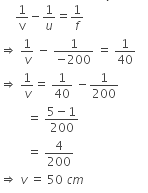
The image will be formed at the focus of an eyepiece lens.
So, for normal adjustment distance between objectives and eyepiece (length of tube) will be, v + Fe = 50 + 4 = 54 cm
Q8: Match the corresponding entries of column 1 with column 2. [Where m is the magnification produced by the mirror]
Column - 1 Column - 2
(A) m = -2 (a) Convex mirror
(B) m = -1/2 (b) Concave mirror
(C) m = +2 (c) Real image
(D) m = =1/2 (d) Virtual image
(a) A → c and d; B → b and d; C → b and c; D → a and d
(b) A → b and c; B → b and c; C → b and d; D → a and d
(c) A → a and c; B → a and d; C → a and b; D → c and d
(d) A → a and d; B → b and c; C → b and d; D → b and c
Ans: (b)
Solution:
(A) m = -2, so the image is magnified and inverted. Which is possible only for concave mirrors. since the image is i inverted it will be real.
(B) M = -1/2, so the image is inverted and diminished. since the image is inverted, so it will be real, and the mirror will be concave.
(C) M = +2, the image is magnified so the mirror will be concave. The image is erect so it will be virtual.
(D) m = +1/2, the image is erect so the image will be virtual. The image is virtual and diminished, so the mirror should be convex.
Q9: The angle incidence for a ray of light at a refracting surface of a prism is 45 degrees. The angle of the prism is 60 degrees If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are
(a) 30 deg; 1/√2
(b) 45 deg; 1/√2
(c) 30 deg; √2
(d) 45 deg; √2
Ans: (c)
Solution:

2015
Q1: In an astronomical telescope in normal adjustment a straight black line of length L is drawn on inside part of objective lens. The eye-piece forms a real image of this line. The length of this image is I. The magnification of the telescope is
(a) 
(b) 
(c) 
(d) 
Ans: (d)

We know, magnification of telescope, we have


Q2: The refracting angle of a prism is A, and the refractive index of the material of the prism is cot (A/2). The angle of minimum deviation is :
(a) 180º + 2A
(b) 180º - 3A
(c) 180º - 2A
(d) 90º - A
Ans: (c)
Solution:



Q3: Two identical thin plano-convex glass lenses (refractive index 1.5) each having a radius of curvature of 20 cm are placed with their convex surfaces in contact at the center. The intervening space is filled with oil of a refractive index of 1.7. The focal length of the combination is :
(a) 50 cm
(b) -20 cm
(c) -25 cm
(d) -50 cm
Ans: (d)
Solution:




2014
Q1: The angle of a prism is A. One of its refracting surfaces is silvered.
Light rays falling at an angle of incidence 2A on the first surface returns back through the same path after suffering reflection at the silvered surface. The refractive index µ , of the prism is
(a) 2 sin A
(b) 2 cos A
(c) 1/2cos A
(d) tan A
Ans: (b)
According to question, diagram is shown below.


Q2: The angle of a prism is ‘A’. One of its refracting surfaces is silvered. Light rays falling at an angle of incidence 2A on the first surface returns back through the same path after suffering reflection at the silvered surface. The refractive index μ, of the prism is :
(a) 1/2 cos A
(b) tan A
(c) 2 sin A
(d) 2 cos A
Ans: (d)
Solution:

Q3: If the focal length of the objective lens is increased then the magnifying power of :
(a) microscope and telescope both will decrease
(b) microscope will decrease but that of telescope will increase
(c) microscope will increase but that of telescope will decrease
(d) microscope and telescope both will increase
Ans: (b)
Solution:

|
97 videos|336 docs|104 tests
|
FAQs on NEET Previous Year Questions (2014-2024): Ray Optics & Optical Instruments - Physics Class 12
| 1. What is Ray Optics and why is it important for NEET preparation? |  |
| 2. What are the key topics in Ray Optics that NEET aspirants should focus on? |  |
| 3. How can previous year NEET questions help in preparing for Ray Optics? |  |
| 4. What are some common types of problems related to Optical Instruments in NEET? |  |
| 5. How do I effectively study Ray Optics for the NEET exam? |  |

|
Explore Courses for NEET exam
|

|


















