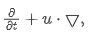Navier-Stokes Equation | Civil Engineering Optional Notes for UPSC PDF Download
| Table of contents |

|
| Navier Stokes Equations – Definition |

|
| Continuity Equation |

|
| Applications of Navier Stokes Equations |

|
| Flow Velocity |

|
Navier Stokes Equations – Definition
The Navier-Stokes equations are fundamental equations in fluid mechanics that describe the motion of viscous fluids. They are a generalization of the equations formulated by Euler for ideal, frictionless, and incompressible fluids. Claude-Louis Navier introduced the concept of viscosity to Euler's equations in 1821 to model more realistic fluid behavior. George Gabriel Stokes further refined this work in the mid-19th century, primarily focusing on two-dimensional flows. However, solutions for more complex three-dimensional flows, which involve turbulence and vortices, have been challenging to find analytically and often require numerical analysis techniques. The Navier-Stokes equations mathematically express the conservation of mass and momentum for Newtonian fluids.
The Navier Stokes momentum equation
The Navier–Stokes momentum equation can be mathematically deduced as a distinct type of the Cauchy momentum equation. The general convective structure is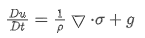
by making the Cauchy stress tensor σ be the sum of a viscosity term τ (the deviatoric stress) and a pressure quantity -pI (volumetric stress), we arrive at,
Cauchy momentum equation (convective structure):

Where
- D/Dt

- ρ = density,
- u = flow velocity,
- ▽ = divergence,
- p = pressure,
- t = time,
- τ = deviatoric stress tensor (order 2),
- “g” denotes material accelerations acting on the continuum (like electrostatic accelerations, inertial acceleration, gravity, etc.)
Continuity Equation
The additional equation that represents the behaviour of fluid is the continuity equation. The equation to the conservation of mass implies the mass of the fluid is neither created nor destroyed in motion. The concept of conservation is an essential principle used throughout classical physics.Continuity equation for flow density,
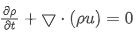
Cauchy momentum equation (conservation structure)
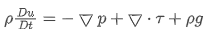
Every non-relativistic balance equation, such as the Navier–Stokes equations, can be constructed by starting with the Cauchy equations and citing the stress tensor with a constitutive relation. By describing the deviatoric stress tensor with fluid velocity gradient and viscosity, and taking fixed viscosity, the Cauchy equations will result in the Navier–Stokes equations.
Applications of Navier Stokes Equations
The Navier-Stokes equations find numerous applications in both applied physics and pure mathematics:Applied Physics:
- Fluid Mechanics: They are used to model various fluid flow phenomena, such as ocean currents, weather patterns, and airflow around wings.
- Engineering: They help in designing vehicles, aircraft, and pipelines, and in analyzing dense liquids and pollution dispersion.
- Power Generation: They are used in designing power plants and understanding fluid dynamics in turbines.
Pure Mathematics:
- Navier-Stokes Smoothness and Existence Problem: The equations are used as a significant unsolved problem in mathematics, which involves proving the consistent existence of smooth solutions in three dimensions.
- Navier-Stokes Millennium Prize: A prize of 1 million US dollars has been offered to anyone who can provide a proof or a counterexample to the Navier-Stokes smoothness and existence problem.
The Navier-Stokes equations are also combined with Maxwell's equations to study and model magnetohydrodynamics, which describes the behavior of electrically conducting fluids, such as plasmas, liquid metals, and saltwater.
Flow Velocity
Flow velocity is a vector field that assigns a velocity vector to each point in a fluid at a given instant in time. This vector represents the magnitude and direction of the fluid's velocity at that point. In general, flow velocity is analyzed in three spatial dimensions, even though two-dimensional and steady-state scenarios are often used as models. Other quantities such as temperature or pressure can be derived from the velocity field using dynamical relations and equations. This differs from classical mechanics, where solutions typically describe the trajectory of a particle.
Solution of Navier-Stokes Equations
In their most general form, the Navier-Stokes equations do not have analytical solutions. Analytical solutions are only possible in certain approximate scenarios, and these solutions may not correspond to real-world systems. More complex systems require numerical techniques, such as computational fluid dynamics (CFD) simulations, to approximate solutions.
|
350 videos|464 docs|2 tests
|
FAQs on Navier-Stokes Equation - Civil Engineering Optional Notes for UPSC
| 1. What are the Navier Stokes Equations and how are they used in fluid dynamics? |  |
| 2. What is the Continuity Equation and how does it relate to the Navier Stokes Equations? |  |
| 3. What are some common applications of the Navier Stokes Equations in real-world scenarios? |  |
| 4. How is flow velocity calculated using the Navier Stokes Equations? |  |
| 5. How can understanding the Navier Stokes Equations be helpful for the UPSC exam preparation? |  |
|
350 videos|464 docs|2 tests
|

|
Explore Courses for UPSC exam
|

|