Numbers and Number System - 1 | Quantitative Techniques for CLAT PDF Download
What is Number System?
The number system or the numeral system is the system of naming or representing numbers. There are various types of number systems in maths like binary, decimal, etc. This lesson covers the entire concepts of the numeral system with their types, conversions and questions.
Numbers and Number System:
Numbers are of many types. These can be defined as given below:
- Numerals: A group of figures is called a numeral. e.g.: 15, 955, -10, -2,
- Natural no.s: The numbers we use for counting the natural objects are known as natural numbers.
These numbers are denoted by N.
So N = (1, 2, 3, 4, 5, 6 ------) Zero is not a natural number. - Whole nos: On including zero (0) in natural no.s, the set of numbers we get, is known as whole nos. and is denoted by W.
So W = ( 0, 1, 2, 3, 4 --------) - Even numbers: The number which is divisible by 2 is called an even number. Such numbers are expressed as 2k (where k is any natural number). Even numbers can be expressed as 2, 4, 6, 8, 10 --------
- Odd numbers: Numbers which are not divisible by 2 are called odd numbers. These numbers are expressed as 2k-1 or 2k+1 (where k is any natural number) example: 1, 3, 5, 7, 9.......
- Prime numbers: A number which is not divisible by any number other than 1 and itself is known as prime numbers. eg: 2, 3, 5, 7, 11..............
1 is not a prime number as it does not have two divisors. - Composite numbers: The no.s other than 1, which are not prime, are called composite no.s.
- Consecutive numbers: A series of numbers is which each number is one more than its predecessor, is called a series of consecutive numbers.
For example:
7, 8 are consecutive nos.
8, 9, 10 are consecutive nos.
56, 57, 58, 59 is a series of consecutive numbers. - Integers: All the +ve whole numbers, all –ve whole no.s and zero are called integers. Eg. -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6..... are all integers. These are denoted by Z.
- Rational numbers: Any number which can be expressed in the form of p/q is known as a Rational Number. p and q are integers and q is not equal to zero. All –ve and +ve fractions, all +ve and –ve decimal numbers and all integers are rational numbers.
- Irrational No.s: The numbers which cannot be expressed in the form of p/q (where p and q are integers and q is not zero) are called irrational no.s. eg:
- Real nos: All rational and irrational no.s. are real numbers eg: -2.3, 0, 5.3 and
- Imaginary nos: Numbers which have only been imagined and cannot be represented on a number line, are called imaginary numbers. They are in the form of bi,
where b is areal number and i=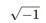 For example
For example - Number line: It is a line on which all the +ve and –ve numbers can be marked.
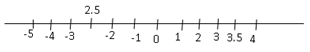
Some Properties of Numbers
- Sum and product of two natural numbers is always a natural number.
- Difference and division of two natural numbers may or may not be a natural number.
- Sum, difference and product of two integers is always an integer.
- (Division of two integers may or may not be an integer.
- Sum, difference, product and the quotient of two rational numbers is a rational number.
- Sum, difference, product and quotient of two irrational numbers may or may not be an irrational number.
- Sum or difference of a rational and an irrational number is an irrational number.
- The product of a non-zero rational number and an irrational number is irrational
- Sum, difference, product and quotient of two real nos. is always a real number.
- Rational number 0 is the additive identity.
i.e. x + 0 = 0 + x = x - Rational number 1 is the multiplicative identity.
a x 1 = 1 x a = a - Every non-zero real number has its multiplicative inverse or reciprocal but ‘o’ has no reciprocal.
- Between any two rational numbers, there is an infinite number of rational numbers.
Other properties of Rational Numbers:
- For each rational number say x, exactly one of the following three is true
(a) x > o
(b) x < o
(c) x = o - For any two rational numbers x and y, exactly one of the following three is true.
(a) x = y
(b) x > y
(c) x < y - If x, y, z, are three rational numbers such that if x > y and y > z then x > z.Question for Numbers and Number System - 1Try yourself:Every rational number is a -View Solution
Comparison of Two Rational Numbers
- Rational numbers having same denominator.
- Rational numbers having different denominators.
(a) If the denominators of two positive rational numbers are the same, the rational number with the smaller numerator is smaller than the other. But for two negative rational numbers, the case will be just the opposite i.e if two negative rational numbers have the same denominator, the rational number with the smaller numerator is greater then the other.
(b) If the denominators of two rational numbers are different, they are first converted into rational numbers having the same denominator, the comparison is based on numerators, not denominators
Ascending and Descending Orders of Rational Numbers
Steps to write two or more rational numbers in ascending or descending order.
Step 1: Write the given rational numbers with +ve denominator.
If given rational number are :
Step 2 : Find the LCM of denominators.
LCM of 10, 8, 3 and 5 is 120.
Step 3: Write all the given rational numbers with this LCM as denominator so that the numbers so written are equivalent to the given rational numbers.
Step 4: Now compare the , so found equivalent rational numbers on the basis of their numerators.
Since -96 < -84 <- 80 < -75
We get
The second method to decide which rational number is greater and which one is smaller.
Let the rational numbers to be compared are
Step I: Cross multiply the numbers i.e.
We get 21 and 25.
Out of 21 and 25, 21 is smaller.
Step II: Find out that this 21 is formed with the help of which numerator. It is 3 of 3/5
Step III: So 3/5 is the smaller rational no.
Note: If the numbers to be compared are three or more, compare the rational numbers by taking pairs.
Multiplicative Inverse of Rational Number
The multiplicative inverse of a non-zero rational number
Also for every non-zero rational number a/b , there exists a rational number
If the product of two rational numbers is 1, then we say that one number is the multiplicative inverse of the other.
Caution: There is no multiplicative inverse for the rational number zero.
Prime numbers: If there is a number which has no divisor apart from 1 and itself, it is called a prime number.
Some Characteristics of Prime Numbers
1) There are 25 prime numbers between 1 and 100 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.
2) 2 is the only even prime number.
3) Between 90 and 100, 97 is the only prime number.
4) 1 is not a prime number. Nor is it a composite no.
To test whether a given number is prime or not.
Step 1. Let the number to be tested be x.
Step 2. Take an integer slightly more than the sq. root of x say y.
Step 3. Test if the given number (x) is divisible by any of the prime numbers less than y
Step 4. If it is not divisible by any of them, then the number x is a prime number., otherwise it is a composite number
Example: Is 377 a prime number?
Solution: 19 is the approximate square root of 377. Prime numbers less than 19 are 2, 3, 5, 7, 11, 13, 17, 377 is divisible by 13.
So, 377 is a composite number.
Difference between Face value and lace value
Face value of a digit in a numeral
The face value of a digit remains as it is and does not change, what ever place it may occupy in the place-value chart. Thus, the face value of 7 is always 7 where ever it may be.
Place value of a digit in a numeral
The place value of a digit in a numeral depends upon the place it occupies in the place-value chart.
If 5 occurs at one's place, its place value = 5 ones = 5 x 1=5
If 5 occurs at ten's place its place value = 5 x 10=50
If 5 occurs at hundreds place, its place value= 5 hundreds = 5 x 100=500 and so on.
Example: Consider the numeral 5439602
Solution: In this numeral
Place value of 2 is = 2 ones = 2 x 1=2
Place value of 0 is = 0 tens = 0 x 10 = 0
Place value of 6 is = 6 hundreds = 6 x 100 = 600
Place value of 9 is = 9 thousands = 9 x 1000 = 9000
Place value of 3 is = 3 ten thousands = 3 x 10000 = 30,000
Place value of 4 is = 4 lakhs = 4 x 100000 = 400000
Place value of 5 is = 5 ten lakhs = 5 x 10,00000 = 50,00000
|
49 videos|174 docs|73 tests
|
FAQs on Numbers and Number System - 1 - Quantitative Techniques for CLAT
| 1. What is a number system? |  |
| 2. How does the decimal number system work? |  |
| 3. What is the binary number system? |  |
| 4. How does the hexadecimal number system work? |  |
| 5. What are the advantages of using different number systems? |  |






















