Quantum Numbers, Orbitals & Their Shapes | Chemistry Class 11 - NEET PDF Download
| Table of contents |

|
| Quantum Numbers |

|
| Orbitals |

|
| Shapes of Atomic Orbitals |

|
| Understanding Atomic Orbitals through Boundary Surface Diagrams |

|
Quantum Numbers
In the solution to the Schrodinger equation for the hydrogen atom, three quantum numbers arise from the spatial geometry of the solution and a fourth arises from electron spin.
No two electrons can have an identical set of quantum numbers according to the Pauli exclusion principle, so the quantum numbers set limits on the number of electrons that can occupy a given state and therefore give insight into the building up of the periodic table of the elements.
(1) Principal Quantum No. (n) :
The principal quantum number or total quantum number n arises from the solution of the radial part of the Schrodinger equation for the hydrogen atom. The bound state energies of the electron in the hydrogen atom are given by En
- Permissible values of n: all integers from 1 to ∞ (infinity).
- This no. identifies the shell in an atom.
- It gives an idea of average distance `R' [size of any orbital from the nucleus higher the value of, n, the higher the average distance and hence greater will be the size].
- It gives an idea of the energy of electrons up to some extent. The higher the value of n, the higher will be the energy (if `l' is constant). For example order of energy 4s > 3s > 2s > 1s.(v) It gives the value of the total no. of orbitals present in any shell and that is equal to n2.
- It gives the value of the total no. of electrons which may he present in the given shell = 2n2.
- It gives the value of the angular momentum of the electron i.e.

- It gives a variation of radial probability distribution.
(2) Azimuthal Quantum No. or Angular momentum Quantum no. (l)
Permissible values of l is 0 to (n -1). i.e. value of l is restricted by n.n = 1, ℓ = 0
n = 2, ℓ = 0, 1. ; i.e. 2 values of ℓ.
n = 3, ℓ = 0, 1, 2. i.e. 3 values of ℓ.
No. of values of `l' is equal to `n' principal quantum number
It identifies sub shell in an atom
The value of `l' gives the name of the sub-shell and the shape of the orbital.
ℓ | Notation | Name | Shape |
o | s | Sharp | Spherical |
1 | P | Principal | dumbbell-shaped |
2 | d | diffuse | double dumbbell |
3 | f | fundamental | complex |
(3) Magnetic Quantum Number (m)
- The direct implication of this quantum number is that the z-component of angular momentum is quantized according to Lz = mlh/2π
- It is called the magnetic quantum number because the application of an external magnetic field causes a splitting of spectral lines called the Zeeman effect.
- The different orientations of orbital angular momentum represented by the magnetic quantum number can be visualized in terms of a vector model.
(4) Spin quantum number (s) :
- An electron, besides charge and mass, has also spin angular momentum commonly called spin. The spin angular momentum of the electron is constant and cannot be changed.
- An electron spin s = 1/2 is an intrinsic property of electrons. Electrons have intrinsic angular momentum characterized by quantum number 1/2. In the pattern of other quantized angular momenta, this gives total angular momentum
- The resulting fine structure that is observed corresponds to two possibilities for the z-component of the angular momentum.

- This causes an energy splitting because of the magnetic moment of the electron

Orbitals
Orbitals are defined as that region or zone in the space where the probability of finding electrons is possible (more than 90%). In an atom large no. of permissible orbitals are present.These orbitals are designated by a set of 3 quantum number (n, l, m) which arise as a natural consequence in the solution of Schrodinger equation i.e. the values of 3 quantum numbers are restricted by the solution of Schrodinger equation.
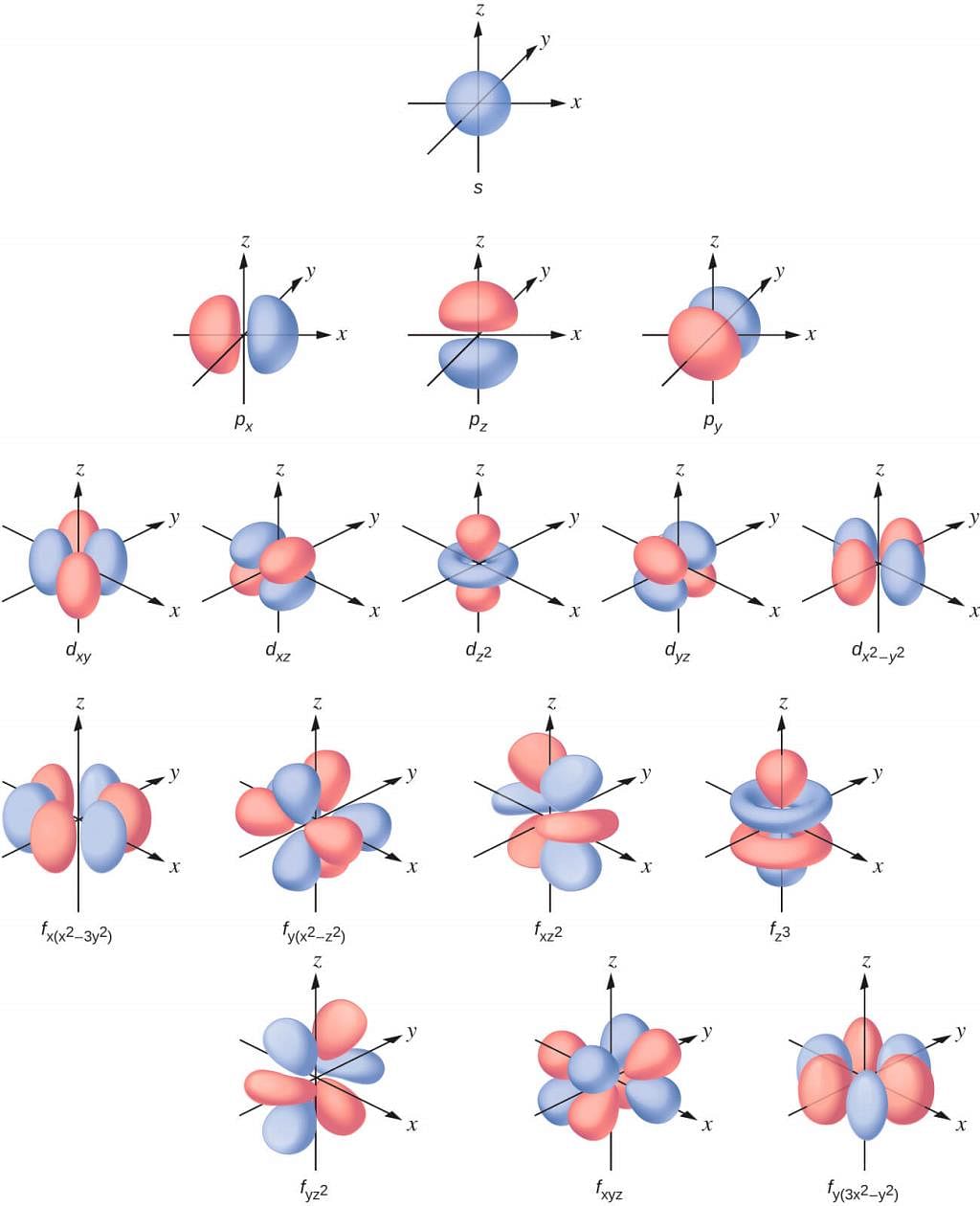 Different Atomic Orbitals
Different Atomic Orbitals
Shapes of Atomic Orbitals
The wave function (ψ) representing an electron in an atom is just a mathematical tool without any physical meaning. It varies for different orbitals, and while it's not something tangible, we can look at plots of these wave functions to understand certain aspects.
According to Max Born, a German physicist, the square of the wave function (ψ²) at a point tells us about the probability density of finding the electron there.

- For example, the probability density of a 1s orbital is highest at the nucleus and drops rapidly as we move away. In contrast, for a 2s orbital, the density decreases quickly to zero, then starts rising again. It reaches a small peak, drops once more, and eventually approaches zero as the distance (r) increases.
- The zones where the probability density becomes zero are called nodal surfaces or nodes. Generally, an ns-orbital has (n – 1) nodes, meaning more nodes appear with an increase in the principal quantum number (n). In simpler terms, a 2s orbital has one node, a 3s has two, and so on.
To visualize these probability density variations, you can look at charge cloud diagrams. Here, the density of dots in a region represents the electron's probability density in that area.
 Charge Cloud Diagram of s-Orbitals
Charge Cloud Diagram of s-Orbitals
Understanding Atomic Orbitals through Boundary Surface Diagrams
Boundary surface diagrams with constant probability density provide a helpful representation of orbital shapes. In this representation, a boundary or contour surface is drawn for an orbital where the probability density |ψ|² remains constant. While many such surfaces are possible, the chosen diagram encloses a region where the probability of finding the electron is high, typically around 90%.
You might wonder why we don't draw a boundary surface diagram enclosing a region with 100% probability of finding the electron. The answer lies in the fact that the probability density |ψ|² always has some value, no matter how small, at any finite distance from the nucleus. Therefore, it's not feasible to draw a fixed-size boundary surface diagram where the probability of finding the electron is 100%.
Sphere for s Orbitals:
- For s orbitals, the boundary surface is essentially a sphere centered on the nucleus, appearing as a circle in two dimensions. This sphere encloses a region where the probability of finding the electron is about 90%.
- Thus, 1s and 2s orbitals are spherical, and in reality, all s-orbitals exhibit spherical symmetry, meaning the probability of finding the electron at a given distance is equal in all directions.
- It's also observed that the size of the s orbital increases with an increase in the principal quantum number (n), following the order 4s > 3s > 2s > 1s. As the principal quantum number increases, the electron is located further away from the nucleus.
 Spheres for s-Orbitals
Spheres for s-Orbitals
2p Orbitals with Lobes
- Boundary surface diagrams for three 2p orbitals (l = 1) are depicted in the figure below. Unlike s-orbitals, these diagrams are not spherical. Each p orbital consists of two lobes on either side of the plane passing through the nucleus.
- The probability density function is zero on the plane where the two lobes touch. While the size, shape, and energy of the three orbitals are identical, they differ in the orientation of the lobes.
- The designations 2px, 2py, and 2pz indicate their alignment along the x, y, or z-axis. Importantly, there's no simple relation between the values of ml (–1, 0, and +1) and the x, y, and z directions. For our understanding, it suffices to remember that due to three possible values of ml, there are three p orbitals with mutually perpendicular axes.
- Similar to s orbitals, p orbitals increase in size and energy with an increase in the principal quantum number. The order of energy and size for various p orbitals is 4p > 3p > 2p. Additionally, like s orbitals, the probability density functions for p-orbitals also pass through zero, both at zero and infinite distance as the distance from the nucleus increases.
- The number of nodes is given by the formula n – 2, where the number of radial nodes is 1 for 3p orbitals, two for 4p orbitals, and so on.
 2p Orbitals
2p Orbitals
d Orbitals and their Shapes:
- For l = 2, the orbital is known as a d-orbital, and the minimum value of the principal quantum number (n) must be 3 since the value of l cannot be greater than n – 1.
- There are five ml values (–2, –1, 0, +1, and +2) for l = 2, resulting in five d orbitals.
- These five d-orbitals are designated as dxy, dyz, dxz, dx²–y², and dz². While the shapes of the first four d-orbitals are similar, the fifth one, dz², differs from the others. Nevertheless, all five 3d orbitals are equivalent in energy.
- The d orbitals for n greater than 3 (4d, 5d, etc.) also have shapes similar to 3d orbitals but differ in energy and size.
 d Orbitals and Their Shapes
d Orbitals and Their Shapes
- Besides the points where the probability density is zero along a line from the nucleus (radial nodes), the probability density functions for the np and nd orbitals are also zero at specific planes passing through the nucleus.
- For instance, in the case of the pz orbital, the xy-plane is a nodal plane. In the dxy orbital, two nodal planes pass through the nucleus and divide the xy plane that contains the z-axis. These planes are called angular nodes, and the number of angular nodes is determined by the quantum number 'l'. For p orbitals, there is one angular node, for d orbitals, there are two, and so on.
- The total number of nodes, which includes both radial and angular nodes, is given by the formula (n–1), where 'n' is the principal quantum number.
|
129 videos|238 docs|88 tests
|
FAQs on Quantum Numbers, Orbitals & Their Shapes - Chemistry Class 11 - NEET
| 1. What are quantum numbers and how do they relate to atomic orbitals? |  |
| 2. What are atomic orbitals and how are they related to the shapes of orbitals? |  |
| 3. How can we understand atomic orbitals through boundary surface diagrams? |  |
| 4. How does the principal quantum number (n) affect the energy level of an electron in an atomic orbital? |  |
| 5. What is the significance of the spin quantum number (ms) in atomic orbitals? |  |

|
Explore Courses for NEET exam
|

|


















