Osmosis, Osmotic Pressure & Van’t Hoff Factor | Chemistry Class 12 - NEET PDF Download
What is Osmosis?
You haven't seen pickles being made at home, have you? That's all there is to osmosis' magic. How does osmosis work, though? Do you realise that osmosis is one of the most important factors in the survival of many species? We will learn everything about osmosis and osmotic pressure in this document.
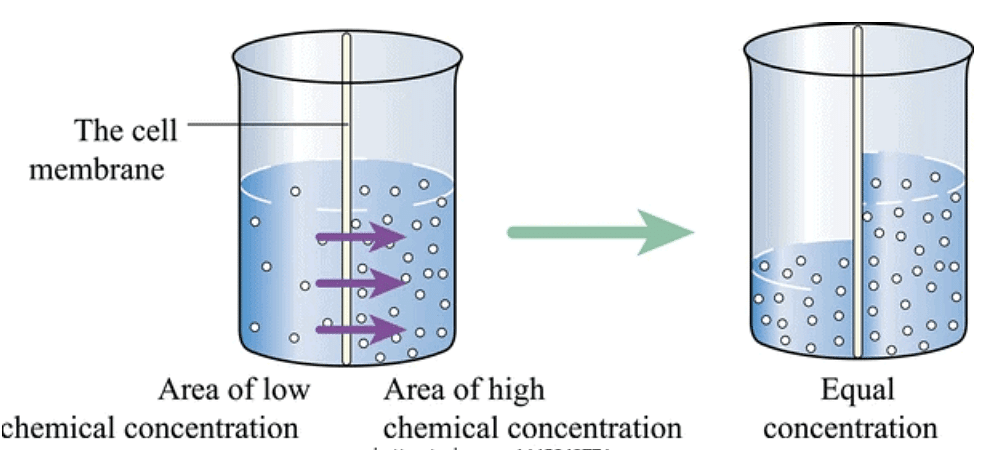
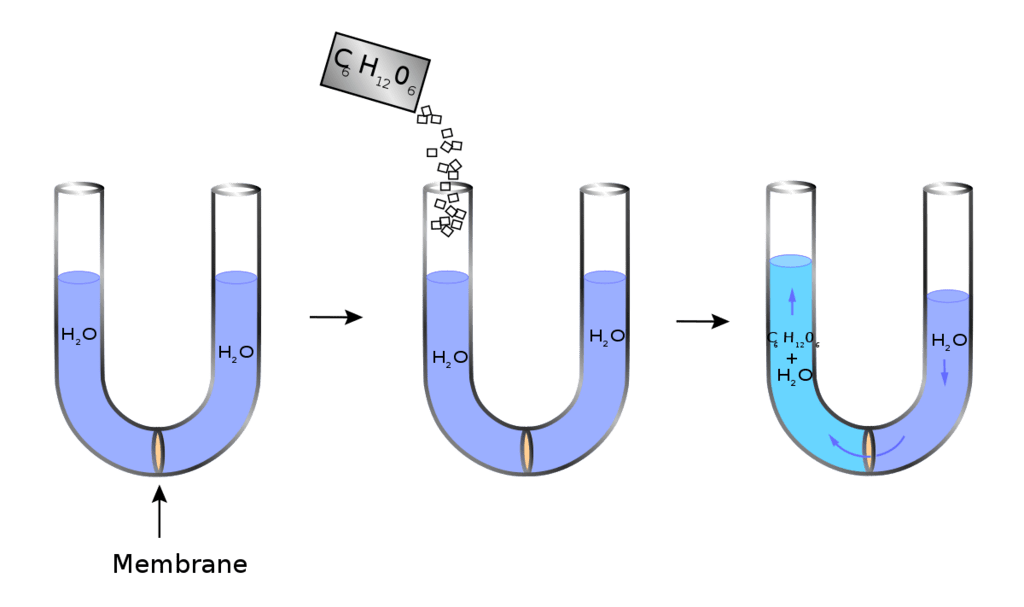
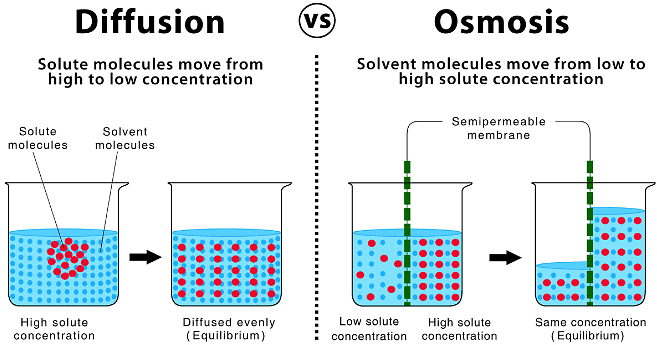
In the process of Osmosis, solvent moves from a region of its higher concentration to a region of its lower concentration through a semi-permeable membrane, which allows the free passage of only solvent molecules.
Osmosis is the phenomenon of solvent flow through a semi-permeable membrane to equalize the solute concentrations on both sides of the membrane.
What is Osmotic Pressure?
Osmotic Pressure can be defined as:
The minimum pressure which should be applied on the solution, so as to prevent the migration of solvent molecules into the solution through a semi-permeable membrane.
 The osmotic pressure p of a solution is related to the molar concentration of solute M as: π = MRT,
The osmotic pressure p of a solution is related to the molar concentration of solute M as: π = MRT,
Where R is the gas constant and T is the absolute temperature.
Van’t Hoff equation for a dilute solution is similar to the ideal gas equation,
πV= nRT
Where π = osmotic pressure
R = gas constant
Some typical examples of osmosis and osmotic pressure are:
(i) The climbing of water up a tall tree from the soil.
(ii) Bursting of red-blood cells when placed in water.
(ii) Swelling of dry raisins when placed in water.
Types of Osmosis
- Exosmosis: This is the outward flow of water from a cell containing an aqueous solution through a semipermeable membrane, e.g. grape in NaCl solution.
- Endosmosis: This is the inward flow of water into a cell containing an aqueous solution through a semipermeable membrane, e.g. grape in water.
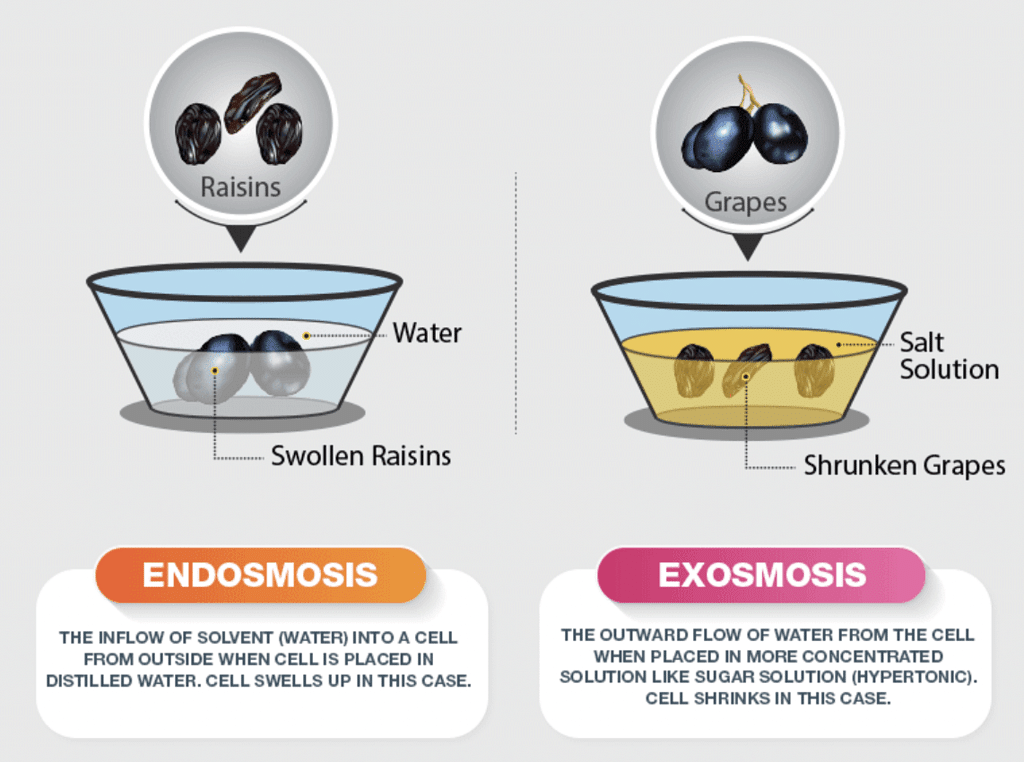
Difference between Endosmosis and Exosmosis
Key concept: The semipermeable membranes allow a selective passage to only the solvent molecules. Cellophane, parchment paper and animal protein membranes are typical semipermeable membranes.
- The most frequently used semipermeable membrane in the laboratory is that of copper ferrocyanide, Cu2[Fe(CN)6] because it is very strong and can withstand very high pressure.
- Remember that the semipermeable membrane of Cu2[Fe(CN)6] does not work in non-aqueous solution because it gets dissolved in nonaqueous solvents.
- Another synthetic semipermeable membrane is that of calcium phosphate.
- Natural semipermeable membranes are cell walls, pig’s bladder, the skin surrounding white of an egg, the membrane surrounding RBCs etc.
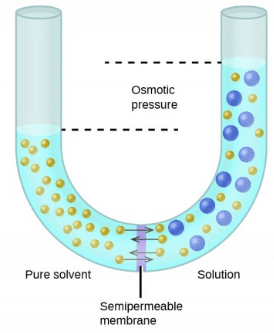
The hydrostatic pressure set up as a result of osmosis is a measure of the osmotic pressure of the solution.
For instance, if the solution of density d rises to height h, then osmotic pressure is expressed as π = h × d × g, where g is the acceleration due to gravity.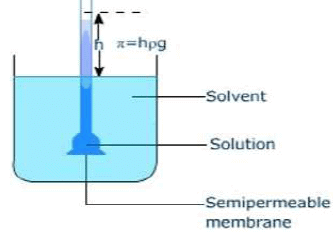
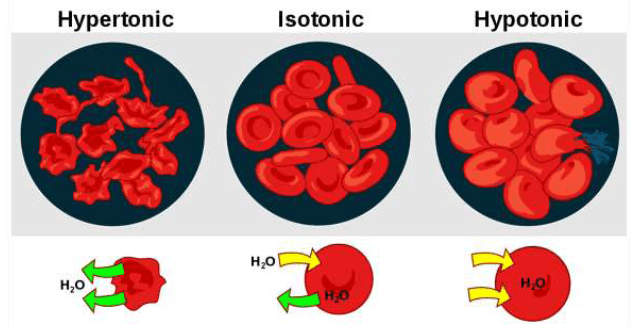
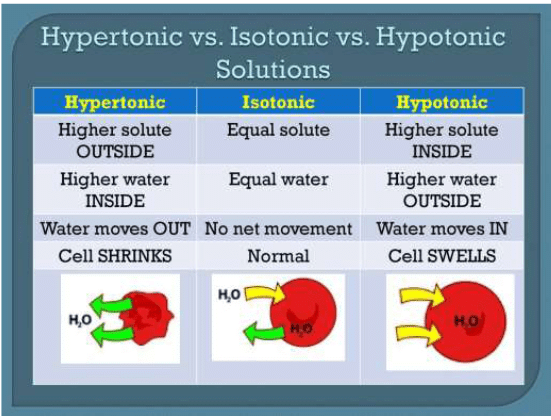
Tonicity
The ability of an extracellular solution to make water move into or out of a cell by osmosis is known as its tonicity.
Three terms—hypertonic, hypotonic, and isotonic—are used to describe whether a solution will cause water to move into or out of a cell:
Isotonic Solution
A pair of solutions having the same osmotic pressure are known as isotonic solutions.
- If two such solutions are separated by a semipermeable membrane, there will be a transference of solvent from one solution to the other.
- Isotonic solutions have the same concentration.
- 0.85% NaCl solutions are found to be isotonic with blood, while 0.9% NaCl solution isotonic with human RBCs.
For isotonic solution, π1 = π2
Or C1 = C2 ⇒ n1/V1 = n2/V2
or W1/m1V1 = W2/m2V2
Hypertonic Solution
If a cell is placed in a hypertonic solution, there will be a net flow of water out of the cell, and the cell will lose volume. A solution will be hypertonic to a cell if its solute concentration is higher than that inside the cell, and the solutes cannot cross the membrane.
When placed in hypertonic solutions, the fluid from the plant cells comes out and thus the cells contract in size (plasmolysis). When excess fertilizers (like urea) are applied, plasmolysis takes place and plants dry up (wilt).
Hypotonic Solution
If a cell is placed in a hypotonic solution, there will be a net flow of water into the cell, and the cell will gain volume. If the solute concentration outside the cell is lower than inside the cell, and the solutes cannot cross the membrane, then that solution is hypotonic to the cell. When placed in water or hypotonic solutions, cell swell and burst (haemolysis).
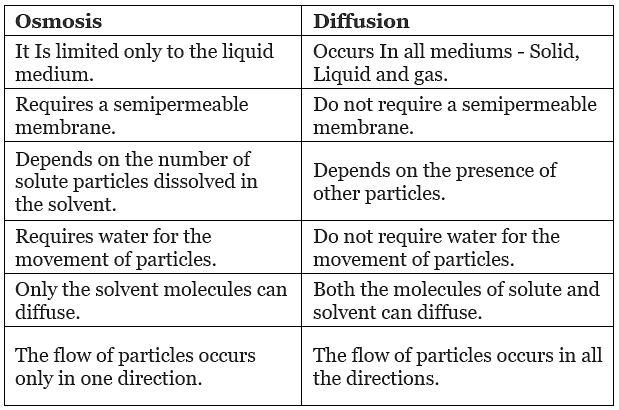
Comparison Between Diffusion And Osmosis
Difference between Osmotic Pressure and Vapour Pressure

Example 1. Calculate the osmotic pressure and vapour pressure of 0.6% aqueous solution of a non-volatile, non-electrolyte solute, urea (NH2CONH2) at 25˚C. The vapour pressure of pure water at 25˚C is 24 mm Hg. Take densities to be 1 g mL-1 and assume ideal behaviour of the solution. Gas constant, R = 0.082 L atm. mol-1 K-1.
Key concept: Please refer to difference between osmotic pressure and vapour pressure while solving this illustration.
Solution.
Concentration of urea solution = 0.6%
This means, solution contains 0.6 g of urea per 100 g, and hence 100 mL of the solution,
So,
Mass of urea per litre of solution
= 0.6/100 × 100 = 6 g
Molar mass of urea, M = 60 g/mol
Concentration of urea in solution
= 6/60 mol/L = 0.1 mol/L
Example 2. At 25˚C, the osmotic pressure of human blood due to the pressure of various solutes in the blood is 7.65 atm. Assuming that molarity and molality are almost same, calculate the freezing point of blood. Kf = 1.86 K kg/mol.
Solution.
According to the Van't Hoff equation,
p = CRT
c = 7.65/(0.082)(298) = 0.313 mol/L
Since molarity and molality are same,
ΔTf = Kfm
ΔTf = 1.86 × 0.313 = 0.582
Freezing point of blood is - 0.582˚C.
Example 3. At 27°C, 36 g of glucose per litre has an osmotic pressure of 4.92 atm. If the osmotic pressure of solution is 1.5 atm at the same temperature, what should be its concentration?
Solution.
Given that,
π1 = 4.92 atm, π2 = 1.5 atm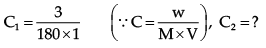
π1V1 = n1RT1
π2V2 = n2RT2
At same temperature,
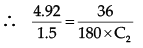
∴ C2 = 0.061 mol/litre
Example 4. At 25°C, a solution containing 0.2 g of polyisobutylene in 100 mL of benzene developed a rise of 2.5 mm at osmotic equilibrium. Calculate the molecular weight of polyisobutylene if the density of the solution is 0.88 g/mL.
Solution.
Height developed = 2.4mm
Osmotic pressure = h.d.g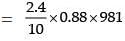
207.187 dyne cm−2
Now πV = nRT
207.187 × 100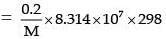
(R in erg; V in mL, using CGS system)
M = 2.39
Try yourself!
What is Reverse Osmosis (RO)?
RO is a process in which a large pressure is applied to the solution side so as to overcome the osmotic pressure.
This pushes the pure solvent under pressure, out of the solution through the semi-permeable membrane. This process finds a number of practical applications. Some of them are the purification of drinking water, removal of salt from water molecules, removal of effluents from water, etc.
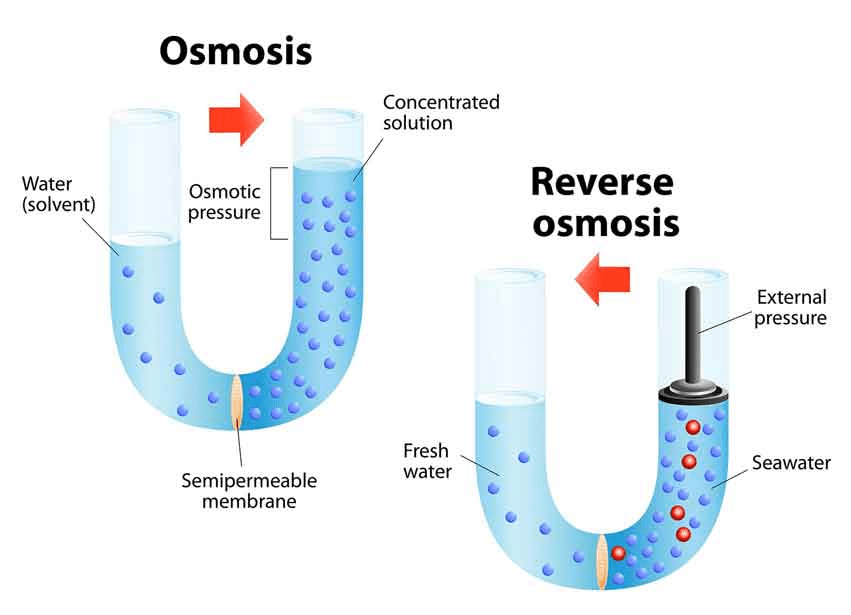
Water Purification
RO is considered one of the most important water purification technologies. The contaminants present in water are removed by pushing water under pressure through a semi-permeable membrane. Pure water is thus squeezed out which is fit for drinking. RO is also used in the desalinization of seawater. RO is a reliable source for obtaining potable water.
- The process eliminates dissolved and suspended impurities, even bacteria.
- The membrane is small enough to allow the solvent molecules to pass but does not allow large ions or molecules to pass through its pores.
- Polymer membranes are used for the desalinization of seawater.
- Cellulose acetate is often used as a semi-permeable membrane. It allows water molecules to pass but is impermeable to impurities.
- It finds application in military, wastewater purification, food industry, landfill leachate purification, etc.
ABNORMAL MOLAR MASS
Molecular masses of the solute can be easily determined with the help of colligative properties; relative lowering in vapour pressure, boiling point elevation, freezing point depression, and osmotic pressure easily. But, we derived the relation between the molecular mass of solute and colligative properties under some assumptions, which are:
- The solution is diluted that is, solvent is available in large amount in order to obey Raoult’s Law
- The solute neither went dissociation or association in the solution
So, how do we determine the molecular mass of solute in case the above assumptions are not valid? Basically, the abnormality is due to:
(i) Association of Solute Particles
- Some solute molecules start to associate inside the solution.
- This means now there are less number of solute particles in the solution.
- As colligative properties vary with solute particles in the solution, they will decrease along with the solute particles.
- As colligative properties are inversely proportional to the molecular mass of solute, we get a higher molar mass of the solute.
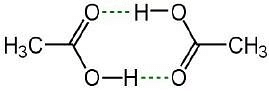
- For Example: Ethanoic acid or acetic acid ( CH3COOH) associate in solution to form a dimer due to hydrogen bonding.

Image 2: Ethanoic Acid dimer due to hydrogen bonding
(ii) Dissociation of Solute Particles
- Some solute molecules, generally electrolytes dissociate into two or more ions/particles when dissolved in a solution.
- This leads to increase in solute particles in the solution, thereby increase in colligative properties of solutions.
- As colligative properties and molecular mass of solute varies inversely, we get a lower molar mass of the solute.
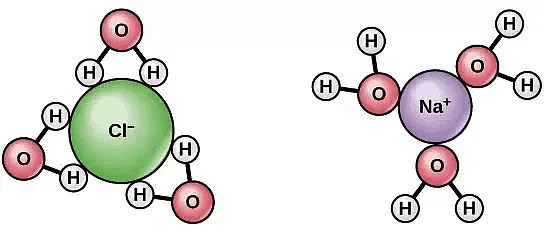 NaCl dissociate into two ions when dissolved in water
NaCl dissociate into two ions when dissolved in water
Van’t Hoff Factor
The Van’t Hoff factor is denoted by ‘i’ and is obtained when we divide normal mass with an abnormal mass of solute. Mathematically, it is represented in three forms:
i = Normal Molar Mass/Abnormal Molar Mass
i = Observed Colligative property/Calculated Colligative property
i = Total Number of Moles of Particles after Association/Dissociation / Total Number of Moles of Particles before Association / Dissociation
Thus, the value of i depends upon the state of solute in the solution.
Following cases become possible.
- When, i = 1, then the solute remains unaffected (i.e., normal) in solution.
- When, i > 1, then the solute undergoes dissociation in solution.
- When, i < 1, then the solute undergoes association in solution.
Thus, for
Potassium chloride (KCl) in aqueous solution, i is nearly equal to 2.
Barium chloride (BaCl2) in aqueous solution, i is nearly equal to 3.
Benzoic acid (C6H5COOH) in benzene, i is nearly equal to 0.5.
Acetic acid (CH3COOH) in benzene, i is nearly equal to 0.5.
Calculation of I (Van’t Hoff Factor)
First, we write an equation of the solute being associated or dissociated
CASE 1: WHEN SOLUTE UNDERGOES DISSOCIATION WHEN DISSOLVED IN SOLVENT
Degree of dissociation: It is defined as the number of moles dissociated over the initial number of moles taken.
Van’t Hoff factor = Total number of particles at equilibrium/Total initial number of particle
Let c moles per litre of an electrolyte AxBy be taken and let it dissociated as
AxBy →xAy+ + yBx–
t = 0 C 0 0
c (1 − α) xcα ycα At equilibrium
i = concentration or number of moles after dissociation/concentration or number of moles before dissociation
i =[c - cα + xcα + ycα ]/c
or i = [1 - α + xα + yα ]/1
= 1 + [(x + y)–1]α
Let x + y = n = number of particles formed after dissociation
i = 1 + (n – 1)α
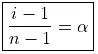
Degree of Association may be defined as the number of molecules associated per unit volume over initial concentration
i = Total number of particles or concentration after association/Total number of particles or concentration before association
Let n molecules of an electrolyte A undergo association
then, nA → An
C 0 t = 0
C – C · α C.α/n At. equilibrium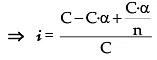
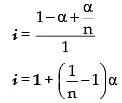
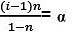 |
MODIFIED EQUATIONS FOR COLLIGATIVE PROPERTIES
For solutes which undergo dissociation or association in solutions, the equations for the colligative properties are modified by inserting the van'tHoff's factor in them as follows: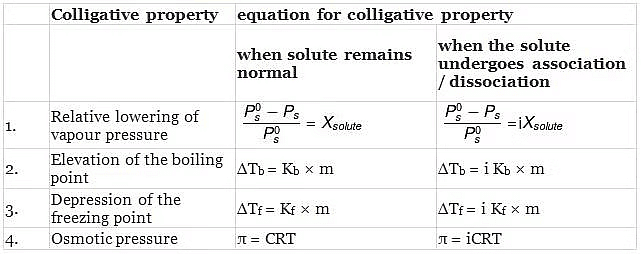
Example 1. Acetic acid (CH3COOH) associates in benzene to form double molecules. 1.65 g of acetic acid when dissolved in 100 g of benzene raised the boiling point by 0.36˚C. Calculate the Van't Hoff factor and the degree of association of acetic acid in benzene. (Kb = 2.57 K kg mol -1).
Solution.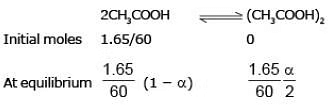 Total moles at equilibrium
Total moles at equilibrium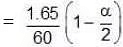 ∆Tb = Kb × m,
∆Tb = Kb × m,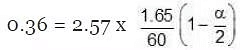 α = 0.981Van't Hoff factor = no. of moles at equilibrium/Initial no. of moles
α = 0.981Van't Hoff factor = no. of moles at equilibrium/Initial no. of moles
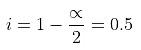 Example 2. Derive a relationship between Kb, Tb and ∆Hvap for a liquid.
Example 2. Derive a relationship between Kb, Tb and ∆Hvap for a liquid.
Solution.
Let us consider a pure liquid. At its boiling point, Tb, its vapour pressure P˚ would be equal to the external pressure.
P˚ = Pext at temperature Tb.
Now let us consider a non-volatile solute dissolved in the liquid. When the solution reaches temperature Tb, the vapour pressure of the system, would be less than the external pressure. When the solution is heated further and it reaches its boiling Tb, the vapour pressure of the solution would be equal to Pext which is equal to the P˚ of the pure liquid at its boiling point. Since vapour pressure of a system are the Kp's for the respective equilibrium,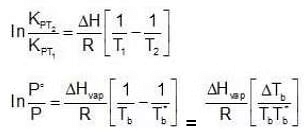 Assuming the solution to be highly dilute, Tb would be very close to Tb.
Assuming the solution to be highly dilute, Tb would be very close to Tb.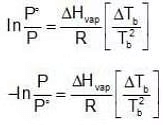
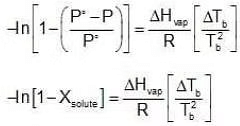 Since Xsolute is very small, we can make the approximation that in (1 - x) = -x (when x is very small).
Since Xsolute is very small, we can make the approximation that in (1 - x) = -x (when x is very small).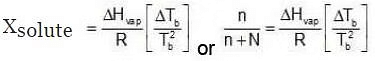 Ignoring n in comparison to N in the denominator
Ignoring n in comparison to N in the denominator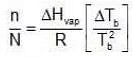
 Multiplying by 1000 on both the sides, we get,
Multiplying by 1000 on both the sides, we get,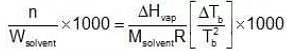
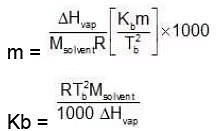 Similarly, Kf =
Similarly, Kf = 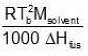 Example 3. To 500 cm3 of water, 3.0 × 10- 3 kg of acetic acid is added. If 23% of acetic acid is dissociated, what will be the depression in freezing point? Kf and density of water are 1.86 K kg-1 mol-1 and 0.997 g cm-3 respectively.
Example 3. To 500 cm3 of water, 3.0 × 10- 3 kg of acetic acid is added. If 23% of acetic acid is dissociated, what will be the depression in freezing point? Kf and density of water are 1.86 K kg-1 mol-1 and 0.997 g cm-3 respectively.
Solution. Molality of acetic acid
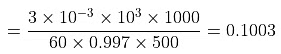 Total number of moles per kg of solvent = 0.1003 (1 + 0.23)ΔTf = Kfm = 1.86 × 0.1003 × 1.23 = 0.23o C
Total number of moles per kg of solvent = 0.1003 (1 + 0.23)ΔTf = Kfm = 1.86 × 0.1003 × 1.23 = 0.23o C
Example. 4. At 300 K, the vapour pressure of an ideal solution containing one mole of A and 3 moles of B is 500 mm of Hg. At the same temperature, if one mole of B is added to this solution, the vapour pressure of the solution increases by 10 mm of Hg. Calculate the V.P. of A and B in their pure state.
Solution.
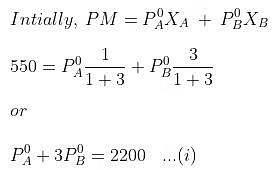
When, one mole of B is further added to it,
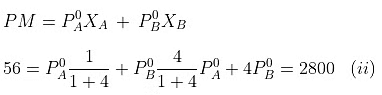 Solving equations (i) and (ii), we getP°A= 440 mm, P°B= 600 mm
Solving equations (i) and (ii), we getP°A= 440 mm, P°B= 600 mm
Example 5. A decinormal solution of NaCl exerts an osmotic pressure of 4.6 atm. at 300 K. Calculate its degree of dissociation. (R = 0.082 L atm. K-1mol-1).
Solution.
No. of moles of NaCl per litre of solution = 0.1
Osmotic pressure (p) = 4.6 atm., Temperature (T) = 300 K
Had NaCl not dissociated, then
p normal = CRT = 0.1 × 0.082 × 300 atm. = 2.46 atm.
But, pobs = 4.6 atm.
As per definition,
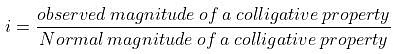
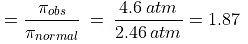
For the dissociation of an electrolyte producing n ions,
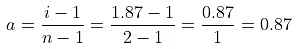 So, Percentage dissociation = 100 × a = 100 × 0.87 = 87%
So, Percentage dissociation = 100 × a = 100 × 0.87 = 87%
Example 6. Vapour pressure of C6H6 and C7H8 mixture at 50˚C are given by: P = 179 XB 92, where XB is mole fraction of C6H6. Calculate (in mm):
(A) Vapour pressure of pure liquids.
(B) Vapour pressure of liquid mixture obtained by mixing 936 g C6H6 and 736 g toluene.
(C) If the vapours are removed and condensed into liquid and again brought to the temperature of 50˚C, what would be mole fraction of C6H6 in vapour state?
Solution.
(A) Given, P = 179XB + 92
For pure, C6H6, XB = 1
P°B= 179 + 92 = 271 mm
For pure C7H8, XB = 0
P°T= 179 x 0 + 92 = 92 mm
(B) Now PM = P°BXB + P°TXT
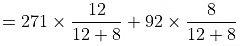 = 162.6 +36.8 = 199.4 mmMoles of C6H6 = 936/78 = 12
= 162.6 +36.8 = 199.4 mmMoles of C6H6 = 936/78 = 12
Moles of C7H8 = 736/92 = 8
(C) Now mole fraction of C6H6 in vapour phase of initial mixture (X'T)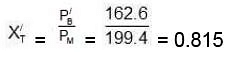 Moles fraction of C7H8 in vapour phase of initial mixture (X'L)
Moles fraction of C7H8 in vapour phase of initial mixture (X'L)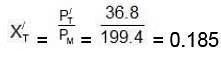
These vapours are taken out and condensed into liquid. The liquid is again brought to 50˚C to get again vapour-liquid equilibrium.
Thus, mole fraction of C6H6 in vapour phase of initial mixture
= Mole fraction of C6H6 in liquid phase on II mixture X'B
Similarly, mole fraction of C7H8 in vapour phase of initial mixture
= Mole fraction of C7H8 in liquid phase on II mixture X'T
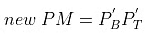 Therefore,
Therefore,
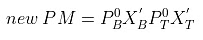 = 271 × 0.815 + 92 × 0.185 mm= 220.865 + 17.02 = 237.885 mm
= 271 × 0.815 + 92 × 0.185 mm= 220.865 + 17.02 = 237.885 mm
New mole fraction of C6H6 in vapour phase
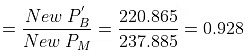
New mole fraction of C7H8 in vapour phase = 0.072.
Example 7. The freezing point depression of an HF (aq) solution with molality 0.10 m is -0.201˚C. What will be the Van’t Hoff factor? Take the value of Kf to be 1.86˚Cm-1
Solution.
HF (aq) → H+ + F-
We have Δ Tf = -0.201 C0 , m = 0.10 and Kf = 1.86 ˚Cm-1
The freezing point depression is Δ Tf = i Kfm
0.201 = i × 1.86 × 0.10
The value of Van’t Hoff factor will be 1.08
Example 8. A millimolar solution of potassium ferricyanide is 70% dissociated at 27°C. Find out the osmotic pressure of the solution.
Solution.
Given, concentration of solution = C = 1/1000 M = 10–3M
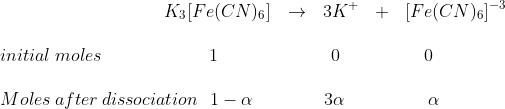
Where α = degree of dissociation = 70% = 70/100 = 0.7
Total moles of after dissociation = (1 – α) + 3α + α = 1+ 3α
∴ i = 1 + 3α/1
i = 1+3α = 1+(3 × 0.7) = 3.1
Since osmotic pressure
π = iCRT
∴ π = 3.1 × 10–3 × 0.0821 × 300
= 0.31 × 3 × 0.0821 atm = 0.07635 atm
TRY YOURSELF!
Q.1. A 0.5 percent aqueous solution of Potassium Chloride was found to freeze at 0.24°C. Calculate the Van't Hoff factor and degree of dissociation of the solute at this concentration (Kf for water is 1.86).
Ans. 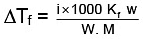
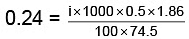
i = 
= 1.923; i = 1+(n–1)α
1.923 = 1+ (2–1)α ⇒ 1.923 = 1+ α
α = 1.923 – 1 = 0.923
or α = 0.923 or 92.3%
Q.2. If the apparent degree of ionization of KCl (KCl = 74.5 gm mol–1) in water at 290K is 0.86. Calculate the mass of KCl which must be made up to 1 dm3 of aqueous solution so as to produce the same osmotic pressure as the 4.0% solution of glucose at that temperature.,
Ans.
Due to ionization of KCl
From question, degree of ionization = a = 0.86
∴ i = 1+ 0.86 = 1.86
For Osmotic pressure of glucose,
For 4% glucose solution,
Weight of glucose = 40 gm,
Volume of solution = V = 1L = 1dm3
Molecular weight of glucose C6H12O6= m = 180 where πglucose = osmotic pressure of glucose
where πglucose = osmotic pressure of glucose Similarly,
Similarly,
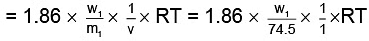 As both solutions are isotonic,∴ πKCl = πglucose
As both solutions are isotonic,∴ πKCl = πglucose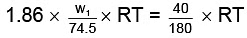
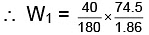 = 8.9 gm
= 8.9 gm
|
108 videos|286 docs|123 tests
|
FAQs on Osmosis, Osmotic Pressure & Van’t Hoff Factor - Chemistry Class 12 - NEET
| 1. What is osmosis? |  |
| 2. What is osmotic pressure? |  |
| 3. What are the types of osmosis? |  |
| 4. What is tonicity? |  |
| 5. What is the difference between osmotic pressure and vapor pressure? |  |

|
Explore Courses for NEET exam
|

|