Overview: Averages | CSAT Preparation - UPSC PDF Download
Importance in CSAT
This chapter is one of the most important chapters of Basic Numeracy for CSAT exams. From the analysis of Previous Years’ Papers, it is clear that direct questions are not asked from this chapter, but its basics are necessary for Data Interpretation. In the year 2024, 2 questions were asked and in 2023, 1 question was asked and in the years 2015-2022 approximately 1-2 questions were asked on the direct application of averages.
What are Averages?
Averages can be defined as the central value in a set of data.
- Average can be calculated simply by dividing the sum of all values in a set by the total number of values.
- In other words, an average value represents the middle value of a data set. The data set can be of anything like age, money, runs, etc.

Example:
What is the average of the first five consecutive odd numbers?
Solution:
The first five consecutive odd numbers are: 1, 3, 5, 7, 9.
Here, the number of data or observations is 5 and the sum of these 5 numbers is 25.
So, average = 25 / 5 = 5.
Applications of Averages
Type I: Average Age
When a person leaves a group and another person joins the group at the place of the person left, then:
(i) In case of an increase in average age,
Age of newcomer = Age of person left + (Number of persons in the group × Increase in average age)
(ii) In case of a decrease in average age,
Age of newcomer = Age of person left - (Number of persons in the group × Decrease in average age)
Example: The average age of a group of 10 friends is 10 years. If one of the friends leaves the group but at his place another friend whose age is 22 years joins the group, the average age becomes 8 years. Find the age of the friend who left the group.
(a) 40 years
(b) 42 years
(c) 44 years
(d) 46 years
Solution: (b)
Explanation:
Age of new friend = Age of friend left - [Number of persons in the group × Decrease in average age]
⇒ 22 = Age of friend left - (10 × (10 - 8))
∴ Age of friend left = 22 + (10 × 2)
= 22 + 20
= 42 years
Type II: Average of Numbers
1. Average Related to Natural Numbers
(i) Average of consecutive natural numbers till n
= (n + 1) / 2
(ii) Average of squares of consecutive natural numbers till n
=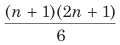
(iii) Average of cubes of consecutive natural numbers till n
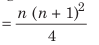
Example: Find the average of squares of the first five natural numbers.
(a) 10
(b) 11
(c) 3
(d) 5
Solution: (b)
Explanation:
Average of squares of the first five natural numbers
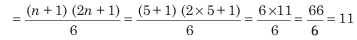
2. Average Related to Even Numbers
(i) Average of n consecutive even numbers = (n + 1)
(ii) Average of squares of n consecutive even numbers =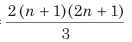
(iii) Average of squares of consecutive even numbers till n =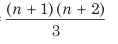
Example: Find the average of squares of consecutive even numbers till 10.
Solution: (b)
Explanation:
Average of squares of consecutive even numbers till 10
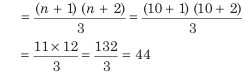
3. Average Related to Odd Numbers
(i) Average of n consecutive odd numbers = n
(ii) Average of consecutive odd numbers till n = (n + 1) / 2
Example: Find the average of consecutive odd numbers till 9.
(a) 4
(b) 5
(c) 7
(d)9
Solution: (b)
Explanation:
Average of consecutive odd numbers till 9
= (n + 1) / 2
= (9 + 1) / 2
= 10 / 2 = 5
Type III Average Speed
1. If a certain distance is covered at a speed of x km/h and the same distance is covered at a speed of y km/h, then the average speed during the entire journey is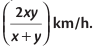
Example: If half of the journey is traveled at a speed of 15 km/h and the next half at a speed of 12 km/h, find the average speed during the entire journey.
Solution:
Average speed= 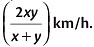
Here, x= 15 and y= 12
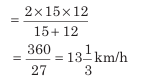
2. If a person or a motor car covers three equal distances at the speed of x km/h, y km/h, and z km/h respectively, then for the entire journey, the average speed of the person or motor car is 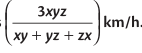
Example: A train covers the first 160 km at a speed of 120 km/h, another 160 km at 140 km/h, and the last 160 km at 80 km/h. Find the average speed of the train for the entire journey.
Solution:
Average speed= 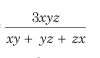
Here, x= 120, y= 140 and z= 80
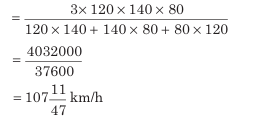
3. If a person covers A km at a speed of x km/h, B km at a speed of y km/h, and C km at a speed of z km/h, then the average speed during the entire journey is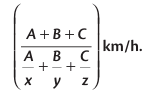
Example: A person covers 9 km at a speed of 3 km/h, 25 km at a speed of 5 km/h, and 30 km at a speed of 10 km/h. Find the average speed for the entire journey.
Solution:
Average speed= 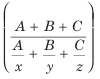
Here, A= 9, B= 25, C=30, x= 3, y=5, z=10
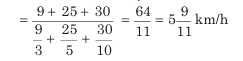
4. If a person covers Ath part of the distance at x km/h, Bth part of the distance at y km/h, and the remaining Cth part at z km/h, then the average speed during the entire journey is
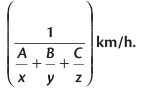
Example: A train covers 50% of the journey at 30 km/h, 25% of the journey at 25 km/h, and the remaining at 20 km/h. Find the average speed of the train during the entire journey.
Solution:
Average Speed= 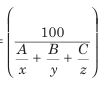
Here, A=50, B=25, C=25, x=30, y=25 and z= 20
Median and Mode
- The median of a finite list of numbers can be found by arranging all the observations from lowest value to highest value and picking the middle one.
- The mode is the value that occurs most often: Mode = 3*Median - 2*Mean

Note:
Sum of 1st n consecutive natural numbers = [n(n+1)]/2
Average of 1st n consecutive natural numbers = (n+1)/2
Shortcut Techniques
Questions based on averages can be easily solved using shortcuts. By using shortcuts, any question can be solved quickly and efficiently which can save a lot of time.1. To find the average or change in average
Example 1:
The average of a batsman in 16 innings is 36. In the next innings, he is scoring 70 runs. What will be his new average?
- a) 44
- b) 38
- c) 40
- d) 48
Solution:
Conventionally solving:
New average = (old sum+ new score)/(total number of innings) = ((16 ×36)+70)/((16+1)) = 38
Shortcut technique:
- Step 1) Take the difference between the new score and the old average = 70 – 36= 34
- Step 2) This is 34 extra runs which are spread over 17 innings. So, the innings average will increase by 34/17 = 2
- Step 3) Hence, the average increases by => 36+2 = 38.Here are a few more average questions and their solutions using the same technique.
Example 2:
The average mark of 19 children in a particular school is 50. When a new student with marks 75 joins the class, what will be the new average of the class?
Solution:
Step 1) Take the difference between the old average and the new marks = 75-50=25
Step 2) This score of 25 is distributed over 20 students => 25/20 = 1.25
Step 3) Hence, the average increases by 1.25=> 50+1.25 = 51.25.
2. Another example where the average dips:
Example 3:
The average age of Mr. Mark’s 3 children is 8 years. A new baby is born. Find the average age of all his children?
Solution:
The new age will be 0 years. The difference between the old average and the new age = 0-8= -8
This age of 8 years is spread over 4 children => (-8/4= -2) Hence, the average reduces to 8-2= 6 years.
3. To find new value when the average is given:
Example 1:
The average age of 29 students is 18. If the age of the teacher is also included the average age of the class becomes 18.2. Find the age of the teacher?
- a) 28
- b) 32
- c) 22
- d) 24
Solution:
Conventionally solving:
Let the average age of the teacher = x(29 × 18 + x × 1)/30Solving for x, we get x = 24.
Shortcut Technique:
Using the shortcut, based on the same method used previously:
Step 1: Calculate the change in average = 18.2 – 18 = 0.2.This change in 0.2 is reflected over a sample size of 30.

The new age is increased by 30 × 0.2 = 6 years above the average i.e. 18 + 6 = 24; which is the age of the teacher.
Method of Deviation to Find the Average
The concept of an assumed mean is not new. It is widely used to reduce the calculation in finding the average in statistics where the data is huge.
Here, We will demonstrate the application of the assumed mean to solve some aptitude questions based on averages and weighted averages.
Let us take an example to understand the concept
Example: In a class of 30 students, the average age is 12 years. If the age of the class teacher is included, the new average age of the class becomes 13 years. Find the age of the class teacher.
Solution:
Standard Approach
Applying the standard approach, the total age of the 30 students = 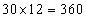 years. When the class teacher is included, the new total age of the class =
years. When the class teacher is included, the new total age of the class =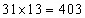 years. Note that the increase in the total age is because of the class teacher only. Hence the age of the class teacher = 403 – 360 = 43 years
years. Note that the increase in the total age is because of the class teacher only. Hence the age of the class teacher = 403 – 360 = 43 years
Deviation method
To understand the deviation method, let us simulate the problem. In the case of average age, assume that each student has 12 chocolates with them.
- The class teacher came up with a few number chocolates and redistribution of the chocolates in the class is done such that every person including the class teacher has the same number of chocolates; which results in 13 chocolates per person (the new average).
- Now, it is obvious that if the class teacher comes with only 12 chocolates, the average remains the same i.e. 12 only (Because he is carrying the number of chocolates which is equal to the average number of chocolates of the group).
- But here with the inclusion of class teachers, the average increases by 1. That means he came with the number of chocolates such that he gave 1 chocolate to each student so that every 30 students now has 13 chocolates.
- Also, in the end, he is left with 13 chocolates for himself so that including him, each member of the class is now carrying 13 chocolates.
Therefore, he came with 30 + 13 = 43 chocolates. Or the age of the class teacher is 43 years.
Important Facts About Averages
- If each number is increased/decreased by a certain quantity n, then the mean also increases or decreases by the same quantity.
- If each number is multiplied/ divided by a certain quantity n, then the mean also gets multiplied or divided by the same quantity.
- If the same value is added to half of the quantities and the same value is subtracted from the other half quantities then there will not be any change in the final value of the average.
Weighted Mean/Average
The weighted arithmetic mean, usually denoted by
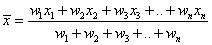 ,
,
where x1, x2, x3, …, xn are averages and w1, w2, w3, .., wn are their respective weight-ages
Example: In a class of 25 boys and 15 girls, the average heights of the two groups of boys and girls are 150 cm and 140 cm respectively. Find the average height of the class.
Solution:
Standard approach:
Total weight of the group of boys = 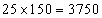 and for the group of girls, the total weight =
and for the group of girls, the total weight =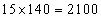 Therefore, the average height of the class =
Therefore, the average height of the class =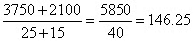
Deviation Approach:
Assume that each boy and each girl is carrying 150 and 140 chocolates respectively.
- We have to distribute the total chocolates such that each boy and girl must carry an equal number of chocolates.
- Since each boy carries 10 chocolates more than each girl, let us take away 10 chocolates from each boy so that now each boy and girl carries 140 chocolates. The excess chocolates we have is equal to
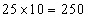 .
. - These excess chocolates are to be equally distributed among the boys and the girls. so, everyone will be getting
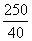 =6.25 more chocolates. Hence the average of the class = 140+6.25 = 146.25 cm.
=6.25 more chocolates. Hence the average of the class = 140+6.25 = 146.25 cm.
Solved Examples
Q1: The average goal scored by 15 selected players in EPL is 16. The maximum number of goals scored by a player is 20 and the minimum is 12. The goals scored by players are between 12 and 20. What can be the maximum number of players who scored at least 18 goals?
a) 10
b) 5
c) 9
d) 6
e) None of these
Solution: Option (c)
To maximize the number of players who scored 18 and above number of goals, one should assume that only one person has scored 20. To counter him, there will be one person who will score 12 goals.
i.e. 15 – 2 = 13 players left.
Now to maximize the 18 and above goals for every two players who are scoring 18, there will be one player scoring 12. This is done, to arrive at an average of 16. We will have 8 players with a score of 18 and 4 players with a score of 12. The last player will have a score of 16 Thus, the maximum number of people with 18 and more goals = 9.
Q2: The average weight of a group of 8 girls is 50 kg. If 2 girls R and S replace P and Q, the new average weight becomes 48 kg. The weight of P= Weight of Q and the weight of R = Weight of another girl T is included in the group and the new average weight becomes 48 kg. Weight of T= Weight of R. Find the weight of P?
a) 48 kgs
b) 52 kgs
c) 46 kgs
d) 56 kgs
Solution: Option (d)
8 x 50 +R+S-P-Q= 48×8 R+S-P-Q=-16
P+Q-R-S= 16 R=S and P=Q
P-R=8
One more person is included and the weight = 48 kg
Let the weight be a = (48 × 8 + a)9/9 = 48
A = 48 kg= weight of R
=> Weight of P= 48+8= 56 kg.
Q3: The average number of goals scored by 15 selected players in EPL is 16. The maximum number of goals scored by a player is 20 and the minimum is 12. The goals scored by players is between 12 and 20. What can be the maximum number of players who scored at least 18 goals?
a) 10
b) 5
c) 9
d) 6
Solution: Option (c)
To maximize the number of players who scored 18 goals or more, one should assume that only one person has scored 20. To counter him, there will be one person who will score 12 goals.
i.e. 15 – 2 = 13 players left.
Now to maximize the 18 and above goals for every two players who are scoring 18, there will be one player scoring 12. This is done, to arrive at an average of 16. We will have 8 players with a score of 18 and 4 players with a score of 12. The last player will have a score of 16 Thus, the maximum number of people with 18 and more goals = 9.
|
205 videos|264 docs|136 tests
|
FAQs on Overview: Averages - CSAT Preparation - UPSC
| 1. What are averages and why are they important in CSAT? |  |
| 2. How do you calculate the mean, median, and mode? |  |
| 3. What are some applications of averages in real-life situations? |  |
| 4. What is the method of deviation to find the average? |  |
| 5. What is the weighted mean and how is it different from the simple average? |  |





















