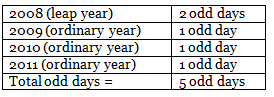Overview: Calendars | Quantitative Techniques for CLAT PDF Download
| Table of contents |

|
| What is Calendar? |

|
| Decoded day of the week |

|
| Evaluation of Leap Year |

|
| Evaluation of Odd Days of a Century |

|
What is Calendar?
A Calendar is a chart or series of pages showing the days, weeks and months of a particular year, or giving particular seasonal information.
Given below is the list of topics under the Calendar section:
- A basic structure of a calendar and a concept of an odd day.
- Decoded days of the weeks.
- Evaluation of a leap year.
- Evaluation of odd days in a century.
- Type 1 problems: Finding the day when another day is given.
- Type 2 problems: Finding the day when another day is not given.
- Type 3 problems: Matching the calendars of a month.
To explore various SBI Exams, check at the linked article.
Basic Structure of a Calendar
- Ordinary year: Any year which 365 days is called an ordinary year.Ex: 1879, 2009, 2019, etc.
- Leap year: Any year which has 366 days is called a leap year.Ex: 2012, 2016 2020 etc.
- The division of the number 365 by 7 gives the quotient 52 and remainder 1 which indicates that an ordinary year has 52 weeks and one extra day. This extra day is referred to as an “odd day” throughout the calendar topics.
- A leap year has 366 days, the division of the number 366 by 7 gives the quotient 52 and remainder 2. This indicates that a leap year has 52 weeks and 2 extra days. These two extra days are also referred to as “odd days”.
Concept of an Odd Day
A number of odd days in a month
January has 31 days, irrespective of whether it’s an ordinary year or leap year. The division of the number 31 by 7 provides the remainder 3 hence January has 3 odd days. On generalising, any month which has 31 days has 3 odd days and any month which has 30 days has 2 odd days.
The only exception happens is in the case of February. The February month of an ordinary year has 28 days, division of 28 by 7 provides zero as remainder. Hence, the number of odd days in February of an ordinary year will have 0 odd days and that of leap year will have 1 odd day as February in a leap year has 29 days.
The below table depicts the number of odd days in different months of a calendar year: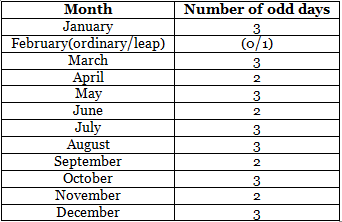 Table 1: List of number of odd days in every month
Table 1: List of number of odd days in every month
Decoded day of the week
The week always begins with Monday and hence Saturday and Sunday are referred to as weekends. In order to make the calculation easier and reduce its time during the exams.
The days of the week are coded as follows: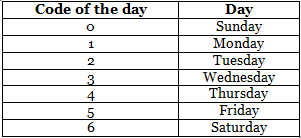
Table 2: The corresponding codes of the day of the week.
This table helps in decoding the answers obtained at the end of the problem-solving process in the calendar topics.
Ex: If the value obtained at the final stage of calculation is 10, then the number 10 is divided by 7 (as we have 7 days in a week) and the remainder which is 3 is decoded back to select the correct options from the given list. Here the remainder 3 indicates the correct answer is Wednesday.
Example 1:
Today is Monday. After 61 days, it will be:
(a) Tuesday
(b) Wednesday
(c) Thursday
(d) Saturday
Sol:
Each day of the week is repeated after 7 days. So,
after 63 days, it will be on Monday.
After 61 days, it will be on Saturday.
Evaluation of Leap Year
The leap year occurs every four years, most of the time, but there are scenarios where the gap between two leap years was 8 years instead of the regular 4 years.
Ex: The year 1896 is a leap year. The next leap year comes in 1904 (1900 is not a leap year).
In order to make the investigation easier and faster, any year which is divisible by number 4 completely (remainder becomes zero) is considered as a leap year.
Ex: 1888, 2012, 2016 are leap years as it’s completely divisible by 4. Years like 2009, 2019 etc. are not divisible by 4 completely hence they normal years.
An exception to note:
A year 700 is completely divisible by 4, but it is not considered as a leap year. For a century year, the logic follows that it should always be divisible by 400 not by 4. Even though the year 700 is divisible by 4 but not by 400. Hence, the year 700 cannot be considered as a leap year.
Ex: 400, 800, 1200 etc. are leap years as they are divisible by 400 and years 300, 700, 100 etc. are not leap years as they are not divisible by 400.
To explore the RRB ALP Syllabus, check at the linked article.
Evaluation of Odd Days of a Century
This concept helps students in answering the question of calendars in less than 30 seconds. The question looks unsolvable, but the application of these concepts makes it easier to solve it in a quicker way.
Observe the question
Q1: What day of the week was year 100 A.D December 31st?
This might look like a difficult and big problem. But it’s definitely not.
Sol: Let’s consider the first 100 years i.e. Year 1.A.D to year 100 A.D
Dividing the first 100 by 4 we get that first 100 years had 76 ordinary years and 24 ordinary years. (The quotient when 100 is divided by 4 gives 25 but the year 100 itself is not a leap year as it is not divisible by 400 hence 24 is considered instead of 25)Step 1: 100 years = 76 ordinary years + 24 leap years
We know that an ordinary year has 1 odd day and a leap year has 2 odd days. Hence, 76 ordinary years will have 76 odd days and 24 leap years will 24*2 = 48 odd days. Adding both the results we get 76+48 = 124 odd days in total.Step 2: 100 years = (76 x 1 + 24 x 2) odd days = 124 odd days.
Dividing the total odd days 124 by 7 gives the quotient as 17 and a remainder as 5. This indicates that 124 days had 17 weeks and 5 odd days.Step 3: 100 years = (17 weeks + days) 5 odd days.
A number of odd days in 100 years = 5.
Now decoding the number to the days of the week from the table gives the result that the number 5 stands for Friday.
Hence, the last day (December 31st) of the year 100 A.D was Friday.
Extension of the logic
Similarly, one can find the last day of the other century years by extending the same logic.
If 100 years had 5 odd days, then logically 200 years should have 10 odd days. Since 10 is greater than 7, the division of 10 by 7 gives the remainder 3. Hence, the 200 years had 3 odd days, which means the last day of the year 200 was Wednesday.
- Number of odd days in 200 years = (5 x 2) = 10 = (7+3) = 3 odd days.
If 100 years had 5 odd days and 200 years 10 odd days logically 300 years should have 15 odd days. The division of 15 by 7 indicates it has 1 odd day from the remainder which indicates it is Monday. Hence, the last day of the year 300 was Monday.
- Number of odd days in 300 years = (5 x 3) = 15 = (14+1) = 1 odd day.
Logically, 400 years should have 20 odd days since 400th year is a leap year as it is divisible by 400. This year will have 20+1 = 21 odd days, which when divided by 7 gives the zero (0) as remainder. Hence, 400 years had 0 odd day and that was Sunday.
The logical approach for the next few years is shown in the table given below: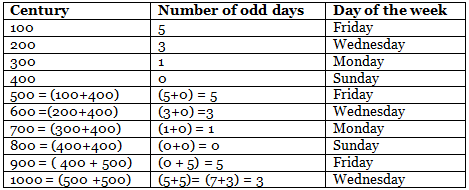
Observations from the table
- The cycle of a number of days repeats after every four centuries and also hence the days at which it ends. The order will always be Friday, Wednesday Monday and Sunday.
- A century will always end on either Friday, Wednesday, Monday or Sunday (Decoded values of these days are 5, 3, 1, and 0 respectively).
- A century will never end on Tuesday, Thursday and Saturday (Decoded values of these days are 2, 4, and 6 respectively).
Type 1 Problems: Finding the day when another day is given
In this section, one has to find out the day of the week of a given date using the day of the week information on the reference date.
Q2: If 17th march 2008 was Monday, what was 1st April 2012?
Sol: The total number of odd days from 17th March 2008 to 17th March 2012.
Since 17th march 2008 was Monday and 17th march 2012 is 5 days more than Monday.
Then adding 5 odd days to Monday, we get Saturday.
Hence 17th march to April 1st we have 15 days.
Saturday+15=Sunday. Adding 15 days or (15 = 14+1) to Saturday, we get the answer as Sunday.
Q3: If today is Sunday, what will be the day on 7777th day?
Sol: If today is Sunday, then the 7th day from today will be Sunday.
Similarly, the 14th day, 21st day or 70th day or 700th day or 7000th day or 7777th day will be Sunday.
Hence, the answer is Sunday.
Type 2 Problems: Find the day when another day is not given
In this section, one has to find out the day of the week of a given date. There will no reference date or day has given here. One can make use of the concept of an odd day to find the answer.
Q4: What day of the week was 15th August 1947?
Sol: The date August 15th 1947 can be divided as follows for easy calculation:
1600 years + 300 years+ 46 years (1901 to 1946) + Jan 1st to august 15th (of 1947)
Note:- Do not write 47 years in the third section, it would indicate 47th year in that century is over.
1600 years + 300 years+ 46 years (1901 to 1946) + Jan 1st to august 15th (of 1947)Now let’s find out the total number of odd days in each section:
Section 1: 1600 is a multiple of 400 years. 400 years have 0 odd days hence 1600 years should have 0 odd days.
Section 2: The second section 30 years will have 1 odd day. Kindly refer to “evaluation of odd days in a century” topic for clarification.
Section 3: This section has 46 years from 1901 to 1946, we know that an ordinary year has one odd day and a leap year has 2 odd days.Let’s first calculate the total number of leap years from 1901 to 1946.
Division of 46 by 4 gives the quotient as 11, which indicates that from 1901 to 1946 we have 11 leap years. If there are 11 leap years among 46 years then remaining 35 years should be ordinary years. Hence, 35 ordinary years will have 35 odd days and 11 leap years will have 11*2 = 22 years.
The total number of odd days in 46 years will be 35+22 = 57 odd days. The division of 57 by 7 given the remainder as 1.This indicates from 1901 to 1946 there is only one odd day.Section 4: It has months from January to August 15th. We have already calculated the total number of odd days in each month in the odd day’s section.
Since 1947 is not a leap year February had zero odd days.
Check the table below for a better understanding of the number of odd days in a month:The total number of odd days is 31 which when divided by 7 gives the remainder 3. Hence, the total number of odd days in the year 1947 from January 1st to August 15th is 3.
Adding the total number of odd days of each section:The total number of odd days = 0+1+1+3 = 5 = Friday. Hence, August 15th 1947 was Friday.
Type 3 Problems: Matching the Calendar
Q5: Which year in the future will have the same calendar exactly as 2009?
(a) 2010
(b) 2013
(c) 2015
(d) 2017
Sol: If the total number of odd days between any years is zero or it’s a multiple of seven. Then, those two years will have the same calendar.
The total number of odd days is listed below:Hence, 2015 will have the same calendar as 2009. Option (c) is the correct answer.
|
49 videos|179 docs|73 tests
|