Overview: Geometry, Tables & Graphs | Quantitative Techniques for CLAT PDF Download
Point
A point is an exact location
Line Segment
The straight path between two points A and B is called a line segment AB. A line segment has two end points.
Ray
On extending a line segment AB indefinitely in one direction we get the ray AB. Ray AB has one end point, namely A.
Line
A line segment AB extended indefinitely in both directions is called line AB.
- A line contains infinitely many points.
- Through a given points , infinitaly many lines can be drawn.
- One and only one line can be drawn to pass through two given points A and B.
- Two line meet in a point.
- Two planes meet in a line.
Collinear
In the given figure, the points A,B,C are collinear.

Concurrent Lines
Three or more lines intersecting at the same points are called concurrent lines.
Angle
Two rays OA and OB having a common end points O form angle AOB, written as ∠AOB
Measure of an Angle
The amount of turning from OA to OB is called the measure of ∠AOB written as m(∠AOB).
An angle of 360°
If a ray OA starting from its original position OA , rotates about O in anticlockwise direction and after a complete rotation comes back to its original position , then we say that it has rotated through 360. This complete rotation is divided into 360° equal parts. Then, each part is called 1 degree , written as 1°
1° = 60 minutes, written as 60'
1 minute = 60 seconds, written as 60"
Types of Angle
- Right angle - An angle whose measure is 90° is called a right angle.
- Acute angle - An angle whose measure is less than 90° is called an acute angle.
- Obtuse angle - An angle whose measure is more than 90° but less than 180°, is called an obtues angle.
- Straight angle - An angle whose measure is 180° is called a Straight angle.
- Reflex angle - An angle whose measure is more than 180° but less than 360°, is called a Reflex angle.
- Complete angle - An angle whose measure is 360°, is called a complete angle.
- Equal angle - Two angles are said to be equal , if they have the same measure.
- Complementary angleTwo angles are said to be complementary if the sum of their measures is 90. For example, angles measuring 65° and 25° are complementary angle.
- Supplementary angle - Two angle are said to be supplementary if the sum of their measures is 180°. For example, angles measures 70° and 110° are supplementary.
- Adjacent angle - Two angles are called adjacent angle if they have the same vertex and a common arm such that non-common arms are on either side of the comman arm. In the given figure , ∠AOC and ∠BOC are adjacent angle.
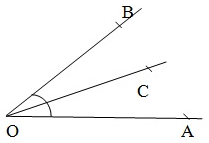
Important Results
If a ray stands on a line , than the sum of two adjacent angle so formed is 180° In the given figure , ray CP stands on line AB.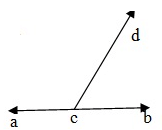
∴ ∠ACD + ∠BCD = 180°.
The sum of all angle around a point is 360° In the given figure five angle are formed around a point O.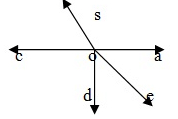
∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA=360°.
Vertically Opposite Angles
If two lines A Band CD intersect at a point O, then AOC , BOD and BOC , AOD are two pair of vertically opposites angle Vertically opposite angle are always equal.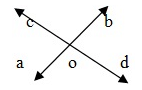 ∴ ∠AOC = ∠BOD and ∠AOD = ∠BOC
∴ ∠AOC = ∠BOD and ∠AOD = ∠BOC
Parallel Lines
If two lines lie in the same plane and do not intersect when produced on either side then such lines are said to be paralleled and we write , L||m.
Traversal line cutting parallel lines
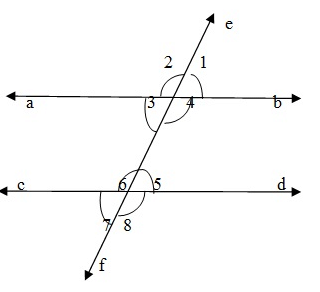 Let two parallel lines AB and CD be cut by a transversal EF. Then Corresponding angle are equal
Let two parallel lines AB and CD be cut by a transversal EF. Then Corresponding angle are equal
(∠1 = ∠5), (∠4= ∠8), (∠2 = ∠6) , (∠3 = ∠7)
Alternate interior angles are equal.
(∠3 =∠5 ) and (∠4 =∠6)
Consective interior angles are supplementary
∠4+∠5 = 180° and ∠3 +∠6 = 180°.
Triangle
A figure bounded by three straight lines is called a triangle. In the given figure , we have ∆ABC; ∆ABC having three vertices A,B,C. In has three angles, namely ∠A,∠B and ∠C. It has three sides , namely AB, AC and BC.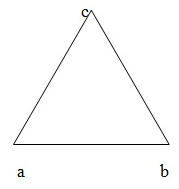
Types of Triangle
- A triangle having all sides equal is called an equilateral triangle.
- A triangle having two sides equal, is called an isosceles triangle.
- A triangle having all sides of different lengths,is called a scalene triangle.
- A triangle one of whose angles measures 90°,is called a right triangle.
- A triangle one of whose angle lies between 90° and 180° is called an obtuse triangle.
- A triangle each of whose angle is acute, is called an acute triangle.
- The sum of all sides of a triangle is called the perimeter of the triangle.
- The sum of two sides of a triangle is greater than the third side.
- In a right angled ABC in which ∠B = 90°, we have AC2 =AB2+BC2. This is called Pythagoras Theorem.
Quadrilateral
A figure bounded by four straight line is called a quadrilateral. The sum of all angles of a quadrilateral is 360°.
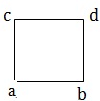
- Rectangle - A quadrilateral is called a rectangle, if its opposite side are equal and each of its angle is 90°. In given fig. ABCD is a rectangle.

- Square - A quadrilateral is called a square, if all of its sides are equal and each of its angles measures 90°. In given fig. ABCD is square in which AB = BC = CD = DA.
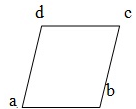
- Parallelogram - A quadrilateral is called a parallelogram, if its opposite sides are parallel. In given fig. ABCD is a parallelogram in which AB = DC & AD = BC.

- Rhombus - A parallelogram having all sides equal is called a rhombus. In given fig. ABCD is a rhombus in which AB =BC =CD=DA, AB || DC and AD || BC.
Important Facts
- A quadrilateral is a rectangle if opposite sides are equal and its diagonals are equal.
- A quadrilateral is a Square if all sides are equal and the diagonal are equal.
- A quadrilateral is a parallelogram, if opposite sides are equal.
- A quadrilateral is a parallelogram but not a rectangle, if opposite sides are equal but the diagonals are not equal.
- A quadrilateral is a rhombus but not a square if all their sides are equal and the diagonals are not equal.
Results on Quadrilateral
- In a parallelogram, we have
- Opposite sides are equal.
- Opposite angles are equal.
- Each diagonal bisects the parallelogram.
- Diagonals of a parallelogram bisect each other.
- Diagonals of a rectangle are equal.
- Diagonals of a rhombus bisect each other at right angles.
Results on Circle
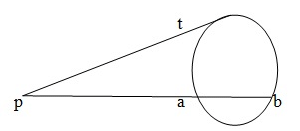
- The perpendicular from the center to a chord bisects the chord.
- There is one and only one circle passing through three non collinear points.
- Angle in a semi circle is a right angle.
- Opposite angles of a cyclic quadrilateral are supplementary.
- Angle in the same segment of a circle is equal.
- The tangent at any point of a circle is perpendicular to the radius through the point of contact.
- Two tangent to a circle from a point outside it are equal.
- If PT is a tangent to a circle and PAB is a secant, Then PA x PB = PT2
What is Data?
Data is the collection of numbers, facts, and figures which have some meaningful interpretation when arranged in a proper way,
For example, The representation of data regarding people below the poverty line helps in providing help to such people.
What is Data Interpretation?
When analysis or interpretation of data is being made to draw some inference and conclusions, it is known as data interpretation.
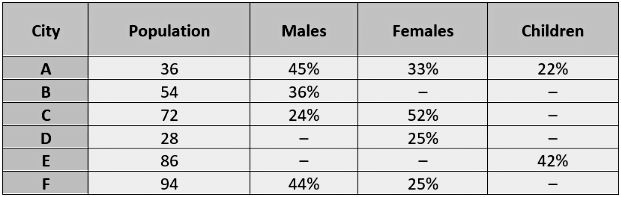
Generally, the question asked from data interpretation are based on the topics ‘Percentage’, ‘Average’, ‘Addition/subtraction’ and ‘Ratio and Proportion’. So, command over calculations and these topics is necessary to score well in this section.
The different methods of arranging data are:
- Tabular Method
- Graphical Method
- CaseLet Form
Tabular Method
In the tabular method, data is arranged in vertical and horizontal rows. It is the easiest way of representing data but not the easiest way of interpreting data. Generally, questions based on tabular method comprises of data regarding Production/Profit/sales of different companies in a year, List of students in a class, list of defective items, Income of different persons, etc.
In the tabular method, either rows or columns are used to represent the discrete non-connected data while other represents connected continuous variable.
For example: In the Representation of Production/Profit/sales of different companies in a year, the production of one company in different years represents connected continuous variables while the production of different companies represents the non-connected discrete variables.
Strategy to solve tabular method DI
Generally, the question asked from Table Data Interpretation (DI) comprise of two kinds of tables: (1) Complete data tables (2) Missing data tables
While solving the missing data table, try to complete the data in the Table if it can be initially completed, as it will help you in solving questions.
To solve the question, first, note down all the variables against which you have to extract the data from Table. E.g., In a table chart comprising of incomes data of 5 persons in 5 years and for solving questions you need data of persons B and C in two years, then just write down all the needed data first and then start solving the question.
Questions from tablular data are basically asked in three forms:
- Addition/Difference based: For table chart comprising of incomes data of 5 persons in 5 years question like find the difference between incomes of two persons in two different years can be asked. These questions are very easy so try to find such question and in case of lack of time go for these questions first.
- Average based: For table chart comprising of incomes data of 5 persons in 5 years question like find the average Income of a person in 5 years can be asked. This type of questions are also easy and require addition skills so can be solved easily.
- Ratio based: Again, the questions from ratio are very easy. You need only addition skills with the knowledge of writing equivalent ratios.
- Percentage based: These questions require a bit of calculation sometimes so should be dealt at the end of the paper in case if lengthy calculations are given.
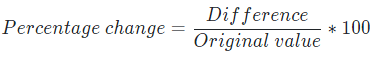
Example 1: Directions: Read the following information carefully and answer the questions accordingly
The following Table represents the population of six different cities (in thousands) and the percentage of males, females, and children among them. It is also given that there is no other person(s) who lie outside the category of males, females, and children. Also, children are exclusive of male and female.
 Q: What is the average number of children in city A, C, E and F?
Q: What is the average number of children in city A, C, E and F?
Sol: Number of children in city A = 22% of 36000 = 7920
Number of children in city E = 42% of 86000 = 36120
Percentage of children in city C = (100 – 24 – 52) = 24%
Number of children in city C = 24% of 72000 = 17280
Percentage of children in city F = (100 – 44 – 25) = 31%
Number of children in city F = 31% of 94000 = 29140
Average number of children
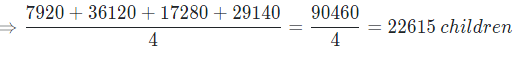
Note: To solve this type of question, one can use approximation and eliminate other options.
Graphical method Data Interpretation
There are different methods to represent data graphically. Some of them are:
Bar Graph
This is the easiest method for both representation and interpretation of data, so it is a widely used method for representation of data. In this method, data is represented through horizontal/vertical rectangles known as a bar. The data representation is through the length of the bars, while the width of the bars does not have any meaning.
Data is represented in a scaled form. Scaling of data means the actual value or amount is shrunk or expanded to a scaled amount so that data fits in the bars easily.
Example 2: Directions: Study the following bar chart carefully and answer the questions given beside.
The bar graph given below represents the number of boys and the number of girls studying in five different colleges.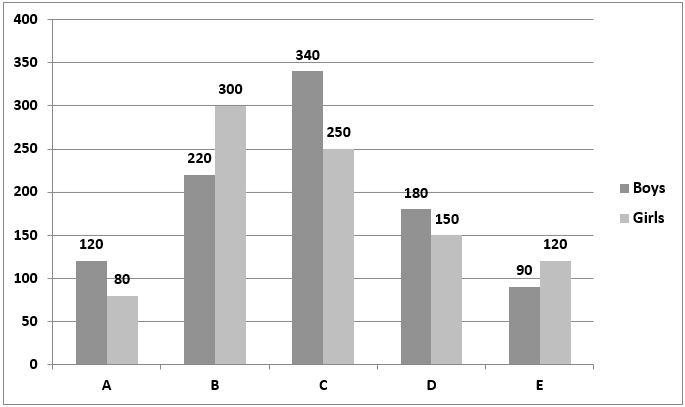
Q: What is the ratio between the sum of the number of boys studying in colleges A, B and C together to the sum of the number of girls studying in the college B, C and D together?
Sol: The number of boys studying in the college A, B, and C together = 120 + 220 + 340 = 680
The number of girls studying in the college B, C, and D together = 300 + 250 + 150 = 700
The required ratio = 680 : 700 = 34 : 35
Line Chart
In this chart, data is represented between Horizontal and vertical axis. Data is represented through a point between the axes, and then points are connected through lines to give it the form of a line chart.
If a line increment upwards between two points, then quantity on point 2 is said to be more than quantity on point 1, and if line decrement downwards between two points, then quantity is said to be decreasing.
The non-connected discrete variables are represented through different line graphs between the same horizontal and vertical axis. For example: If we are representing the production of 3 companies in 5 years, then it will be represented by 3 line graphs.
Line Charts are generally used to show the growth of a company or a product.
Example 3: Directions: The line chart given below shows five dealers A, B, C, D, and E selling three different types of cars (In thousands) viz. Swift, Audi, and WagonR. Read the following line chart and solve the given question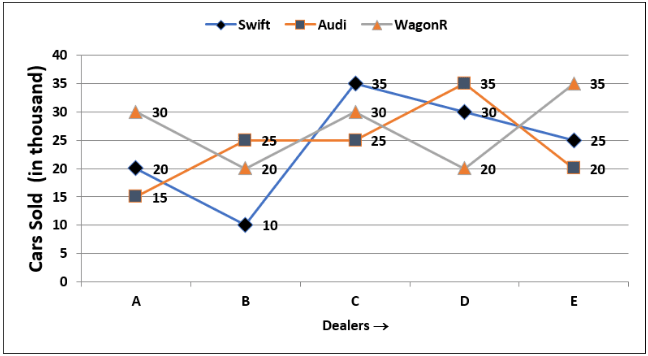 Q: Number of cars sold by A and B is how much percentage more than the cars sold by C?
Q: Number of cars sold by A and B is how much percentage more than the cars sold by C?
Sol: Cars sold by A & B = (65 + 55)
A&B=(65+55) thousand = 1,20,000
Cars sold by C = 90,000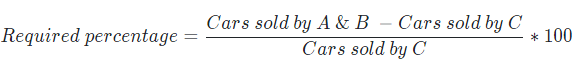

= 33.33%
Pie Chart
- Pie-charts are used to represent the data in a circular manner. It is used generally to represent the continuous variables of different persons/products/company/place etc. in the form of sectors in a circle.
- The whole data in the pie chart is represented in a break-up form or sector or parts. Each part or break up of data comprises of the area in the circle in proportion to the share of it with respect to whole data.
- As the whole data is represented in the form of a circle so, in terms of angles, whole data is represented by 3600. Thus, we can say that area of each sector will be proportional to the central angle.
The central angle of each sector or part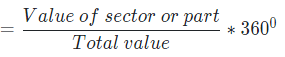
Example 4: Directions: The following pie charts show the distribution of students of graduate and postgraduate levels in seven different institutes in a town.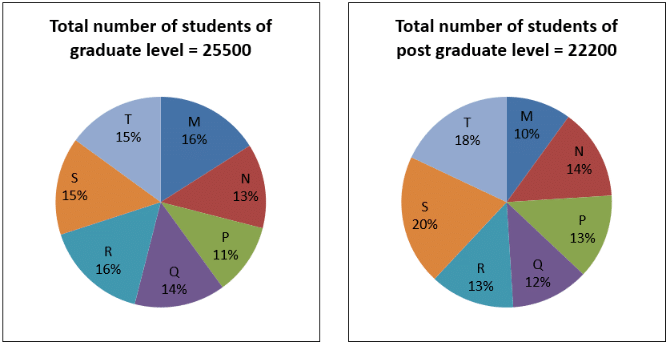
Q. What is the difference between the central angles of non-graduate and graduate students in institute T?
Sol: Value of graduate students in institute T = 15%
Total value of graduate students = 100%
Value of non-graduate students in institute T = 18%
Total value of non-graduate students = 100%
Central angles of non-graduate students in institute T will be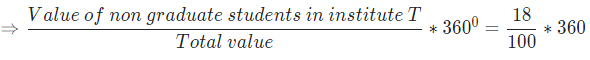
Central angles of graduate students in institute T will be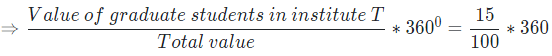
Thus, the required difference = central angles of non-graduate students in institute T - Central angles of graduate students in institute T will be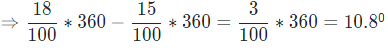
Caselet form
In the Caselet form, data is given in the form of reading comprehension or paragraph. To solve the question, data from comprehension is to be converted in the form of a Table or any other easy representation method.
Example 5: Directions: Study the following information carefully and answer the questions given beside.
Shana visited a shopping centre. She purchased some chocolates of three different brands, namely A, B, and C. The number of chocolates of each brand bought by her was equal to the price of the single chocolate of that particular brand. She has spent a sum of Rs. 602. If she had not bought brand C chocolates, then she would have spent only Rs. 313. Suppose, she purchases brand A chocolates at the price of brand B chocolates, brand B chocolates at the price of brand C chocolate, and the brand C chocolates at the price of brand A chocolates but the number of each brand of chocolates purchased by her remains the same then she spends Rs. 21 less than the price of all the chocolates for the actual price.
Q. What is the average number of chocolates purchased by Shana?
Sol: Let the price of single chocolate of A, B, and C brand chocolate is x, y, and z respectively
Then, according to the question, the number of chocolates of brands A, B, and C that were bought by her are x, y, and z respectively
As we know, that number of chocolates of each brand bought by her was equal to the price of single chocolate of that particular brand, and thus, she spent Rs. 602.
Accordingly, we have
The price of all the chocolates = x ∗ x + y ∗ y + z ∗ z = 602........... (i)
Further, it is known that if she had not bought brand C chocolates, then she would have spent only Rs. 313. Accordingly, we have, x ∗ x + y ∗ y = 313.............(ii)
Equation (i) – (ii)
z ∗z = 289
z = 17
Suppose, she purchases brand A chocolates at the price of brand B chocolates, brand B chocolates at the price of brand C chocolates, and the brand C chocolates at the price of brand A chocolates but the number of each brand of chocolates purchased by her remains the same then
x ∗ y + y ∗ z + z ∗ x = 602 – 21 = 581
We know than, (x + y + z)2 = x2 + y2 + z2 + 2(xy + yz +z x)= 602 + 2 × 581 = 1764
(x+y+z) 2 =1764
x + y + z = 42
x + y = 42 – 17 = 25_______ (iii)_____ (as z = 17)
x2 + y2 + 2xy = (x + y)2
313 + 2xy = 625
2xy = 312
(x–y)2 = (x + y)2 – 4xy = 625 – 624 = 1
x – y =1 ______(iv)
By solving (iii) and (iv)
x = 13, y = 12
Thus, the average number of chocolates purchased by Shana be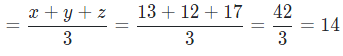
|
49 videos|179 docs|73 tests
|
FAQs on Overview: Geometry, Tables & Graphs - Quantitative Techniques for CLAT
| 1. What is the difference between a point, a line segment, a ray, and a line? |  |
| 2. How are angles formed and measured? |  |
| 3. What does it mean for lines to be parallel? |  |
| 4. How do you classify triangles based on their angles? |  |
| 5. What are some common types of quadrilaterals? |  |





















