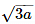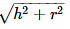Overview: Mensuration | Quantitative Techniques for CLAT PDF Download
| Table of contents |

|
| Mensuration |

|
| Mensuration 3D Formulas |

|
| Hollow Cylinder (Hollow Right Circular Cylinder) |

|
| Differences Between Mensuration 3D and 2D shapes |

|
Mensuration
A section of mathematics that communicates about the length, volume, or area of various geometric shapes is termed Mensuration. These shapes or patterns exist in two dimensions or three dimensions.
Mensuration 3D in Maths- Important Terminologies
Let us discover a few more definitions linked to the various geometric shapes.
Properties of Cube
- All sides are equal.
- The Cube has all six faces in a square shape.
- Each of the faces meets the other four faces.
- The edges opposite to each other are parallel.
- Side = a
Formula for a Cube:
- Volume = a3
- Surface area = 6a2
- Diagonal =

Properties of Cuboid
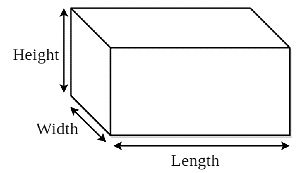
- Three-dimensional shape with length, breadth, and height
- Each of the faces meets the other four faces.
- The edges opposite to each other are parallel.
- Height = h, Length = l and Breadth = b
Formula for a cuboid:
- Volume = l × b × h
- Volume = Area of base × height
- Surface area = 2(lb + bh + hl)
- Diagonal = l2+b2+h2
- Area of four walls = Perimeter of base × height = 2(l + b)× h
- Volume of metal = External volume – internal volume
Properties of Cylinder
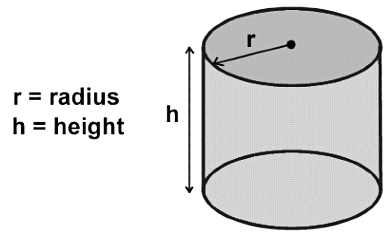
- A cylinder has one curved side.
- A cylinder has two vertical flat ends in the circular shape.
Formula for a cylinder:
- Volume = πr2h
- Surface area = 2πrh
- Total surface area = 2πr(h + r)
Properties of Cone
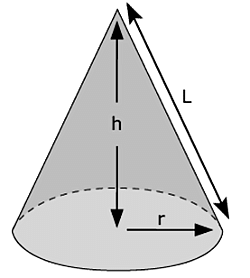
- Height = h, Slant height = l and Radius = r
- It has only one vertex point.
- It’s base is circular.
Formula for a cone:
- Volume = (1/3)πr2h
- l =

- Surface area = πrl
- Total surface area = πr(l + r)
Properties of Sphere
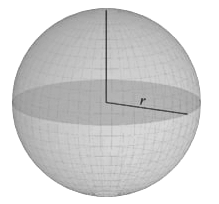
- Volume = 4/3πR3
- Surface area =4πR3
- Volume of metal = 4/3π(R3−r3)
- Volume of hollow sphere = 4/3π(R−a)3
- Here, R = external radius, r = internal radius, a = thinness of wall
Properties of Hemisphere
- Volume = 2/3πr3
- Surface area = 2πr2
- Total surface area = 3πr2
Properties of Prism
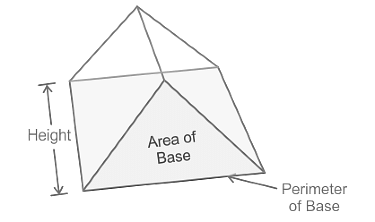
- Volume = Area of base×height
- Lateral surface area = Perimeter of base × slant height
- Total surface area = Perimeter of base × slant height + 2 × Area of base
Mensuration 3D Formulas
With the knowledge of terms, properties and formulas of 3D shapes let us summarise some of the important formulas in the below table, these mensuration formulas are very useful while solving mensuration problems.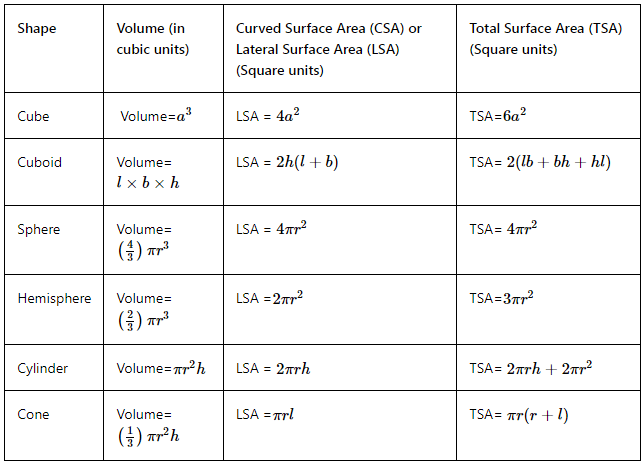
Here’s some more 3D shapes with their formulas and images.
Quarter Sphere
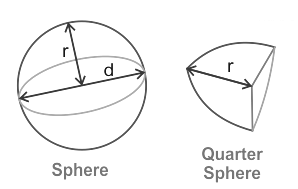
A quarter sphere is specifically one-fourth share of a full sphere. i.e., if we break a sphere into four equal sections, each portion is termed a quarter sphere. Therefore, the volume of a quarter sphere is one-fourth of the volume of a sphere.
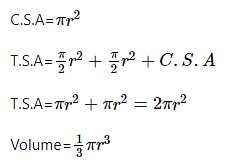
Frustum of a Cone

The frustum of a cone is the section of the cone without vertex when the given cone is split into two pieces with a plane that is parallel to the bottom of the cone.
The frustum of a cone is also called a truncated cone. Similar to any other 3D shape or object, the frustum of a cone also holds surface area and volume. The formula for the same are as follows:


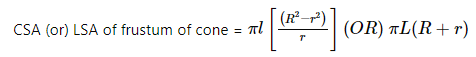
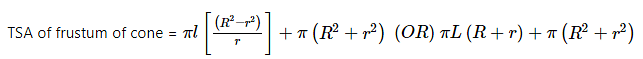
Hollow Cylinder (Hollow Right Circular Cylinder)
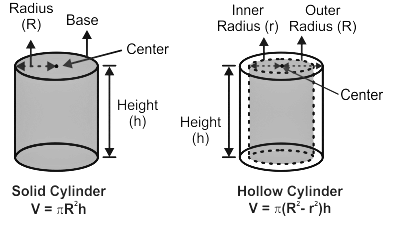
The volume of a hollow cylinder is defined as the 3D space contained by it. For instance, the volume of glass indicates the available area inside it. In other words, we can say that volume represents the maximum space that can be filled by water if the water flows into the glass.
Here the inner radius of the base is ‘r’, the outer radius of the base is ‘R’ and the height of the hollow right circular cylinder is ‘h’.
Volume = πh(R2−r2)
Curved Surface area = 2πRh+2πrh=2πh(R+r)
Total surface area = 2πH(R+r)+2π(R2−r2)
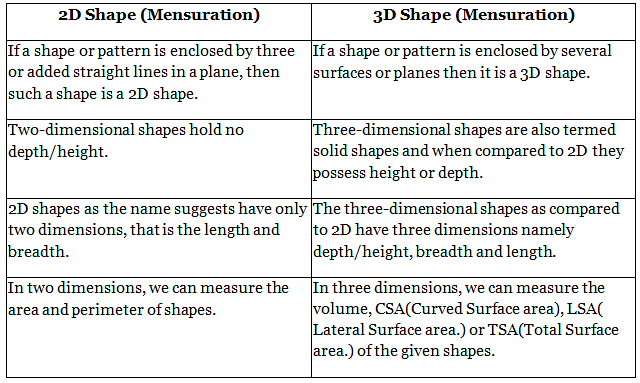
Differences Between Mensuration 3D and 2D shapes
Check out the difference between the Mensuration 2D and 3D shapes.
How to Solve Question Based on Mensuration 3D – Tips and Tricks
Candidates can find different tips and tricks from below for solving the questions related to Mensuration 3D.
- Tip # 1: Make sure you remember all the properties and formulas mentioned above to solve the questions related to this section quickly.
- Tip # 2:Attempt mock and quizzes to brush up your concepts of Mensuration 3D.
Mensuration 3D Sample Questions
Question 1: If the volume of a cube is 4913 cm3, then find the total surface area.
Solution 1: Volume = a3
⇒a3= 4913
∴a = 17 cm
⇒Total surface area = 6a2
∴Total surface area = 6 × 172 = 1734 cm2
Question 2: If the sum of three sides is 45 cm and the length of diagonal is 21 cm in a cuboid, find the total surface area of this cuboid.
Solution 2: l + b + h = 45————— (1)
⇒Diagonal = l2+b2+h2
⇒l2+b2+h2 = 21
⇒l2+b2+h2= 441———— (2)
∴From (1),
⇒(l+b+h)2 = 452
⇒l2+b2+h2 + 2(lb + bh + hl) = 2025 441 + 2(lb + bh + hl) = 2025
⇒2(lb + bh + hl) = 2025 – 441 = 1584 cm2
∴Surface area of this cuboid is 1584 cm2
Question 3: Find the total surface area and volume of a cylinder which has a height of 21m and a base of diagonal is 12m.
Solution 3: Diagonal = 2 × radius Radius = 12/2 = 6 m Total surface area = 2πrh
⇒Total surface area = 2 × 22/7 × 6 × 21 = 792 m2
⇒Volume = πr2h
∴Volume = 22/7 ×62×21=2376 m3
Question 4: The base of a solid right prism is a triangle whose sides are 9 cm, 12 cm and 15 cm. The slant height of the prism is 5 cm, Find the total surface area of the prism.
Solution 4: Perimeter of base = 9 + 12 + 15 = 36 cm Area of base = ½ × 12 × 9 = 54 cm2
⇒Total surface area = Perimeter of base × slant height + 2 × Area of base Total surface area = (36 × 5) + 2 × 54
∴Total surface area =288 cm2.
|
57 videos|108 docs|73 tests
|
FAQs on Overview: Mensuration - Quantitative Techniques for CLAT
| 1. What is mensuration? |  |
| 2. How is mensuration used in real life? |  |
| 3. What are the basic formulas used in mensuration? |  |
| 4. How can I calculate the area of an irregular shape? |  |
| 5. What is the difference between perimeter and area? |  |

|
Explore Courses for CLAT exam
|

|