Overview: Number System | Quantitative Techniques for CLAT PDF Download
Number System
The number system can be understood as a system of writing or expressing numbers in different forms and vice versa. For example binary, decimal, etc. The Hindu–Arabic numeral system is the most widely used, allowing any number to be represented using a combination of 10 fundamental numeric symbols known as digits. It is used in linear algebra, calculus, general mathematics, physics, etc.
History of Numbers and Number Systems
The Egyptians were the first to establish a ciphered number system, and the Greeks were the next to map their counting numerals onto the Ionian and Doric alphabets. Roman numerals, which used combinations of letters from the Roman alphabet, were popular in Europe until the late 14th century when the superior Hindu–Arabic numeral system expanded, and the Hindu–Arabic numeral system is still the most widely used system for representing numbers today.

Number System Definition
A number system presents a unique representation of numbers. It also allows users to perform arithmetic operations like addition, subtraction, and division which play an essential role in computer applications and digital domains. Learn about the basics of the number system, conversion, and implementation.
Types of Number Systems
The four common types of Number systems are
- Decimal Number System: Has base 10.
- Binary Number System: Has base 2.
- Octal Number System: Has base 8.
- Hexadecimal Number System: Has base 16.
Decimal Number System
The decimal number system, which we use every day, uses numbers 0 through 9, i.e. 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Because there are 10 numbers in this number system, the decimal number system’s base number is 10. Any number that is represented without a base has a base of 10. Each value has a power of ten place value, meaning that the digit in the tens place is 10 times bigger than the digit in the one’s place. When we get to 9, we make the rightmost number 0 and add 1 to the left, resulting in 10. We continue to move ahead and so on.
For example, the decimal number 8379 consists of the digit 9 in the unit’s or one’s position, 7 in the tens position, 3 in the hundreds position, and 8 in the thousands position. Its value can be formulated as
(8×1000)+(3×100)+(7×10)+(9×1)(8×1000)+(3×100)+(7×10)+(9×1)
(8×103)+(3×102)+(7×101)+(9×100)(8×103)+(3×102)+(7×101)+(9×100)
8000+300+70+98000+300+70+9
83798379
Binary Number System
The binary number system is a Base-2 numbering system that follows the same mathematical rules as the widely used decimal or base-10 system. Instead of using powers of ten (10n), such as 1, 10, 100, 1000, binary numbers use powers of two (2n), effectively doubling the value of each succeeding bit as it advances, such as 1, 2, 4, 8, 16, 32, and so on.
The binary number system is used by computers to modify and store all of their data, including numbers, words, films, photos, and music. 1 + 1 = 10 since the number “2” does not exist in this system. In 1854, British mathematician George Boole published important work outlining an algebraic logic system based on the binary system, which became known as Boolean algebra.
Octal Number System
The Octal Number System is a number system with an eight-digit base with digits ranging from 0 to 7 i.e., 0, 1, 2, 3, 4, 5, 6, and 7. The term octal is used to describe numbers with an eight-digit base. Octal numbers have a wide range of uses and significance, including in computers and digital numbering systems.
Octal numbers have a wide range of applications and significance, including use in computers and digital numbering systems. When queried by ground radar, airplane transponders broadcast a “squawk” code, which is expressed as a four-octal-digit number. On the radar screen, this code is used to identify different aircraft.
Hexadecimal Number System
Hexadecimal is made up of two words: ‘Hexa’ and ‘deci’, where ‘Hexa’ means six and ‘deci’ indicates ten. The hexadecimal number system is a 16-digit representation of integers 0 through 9 and letters A through F. To put it another way, the first 9 digits or numerals are represented as numbers, while the next 6 digits are represented as symbols from A to F. The hexadecimal number system is extremely similar to the decimal number system, which has a base of nine. After nine numbers, the tenth digit is represented by a symbol: 10 as A, 11 as B, 12 as C, 13 as D, 14 as E, and 15 as F.
The Base16 transfer encoding uses the hexadecimal system to divide each byte of plaintext into two 4-bit values and two hexadecimal digits. Because they give a human-friendly representation of binary-coded data, hexadecimal numbers are widely employed by software engineers and system designers. Four bits (binary digits) are represented by each hexadecimal digit, also known as a nibble (or nybble).
Number System Chart

Conversion in Number System
The number systems decimal, binary, octal, and hexadecimal are all positional value number systems. To convert a binary, octal, or hexadecimal number to a decimal number, just multiply each digit by its positional value. We’ll learn how to convert between various number systems in this section.
Decimal to Binary
By repeatedly dividing a number by two and recording the result, decimal values can be transformed into binary. Steps to be followed:
Conversion of Integer Decimal Numbers to Binary
- Divide the number by 2.
- Get the integer quotient for the next iteration.
- Get the remainder for the binary digit.
- Repeat the above steps until the quotient is equal to 0.
Solved Example
Let’s convert 29 to Binary
We repeatedly divide 29 by 2 till we get 0 reminders.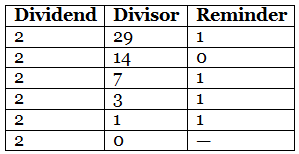
We read the reminder in reverse order. So 2910=101112
Next is the conversion of the fraction part.
Conversion of Fractional Decimal Numbers to Binary
A fraction is made of a whole part and a decimal part. For the conversion of the whole part to binary, follow the same steps as mentioned above. For the fractional part, follow the steps below:
- Multiply two to the fractional part of the decimal number.
- The whole part of the product is our binary equivalent.
- Step 1 is repeated using only the fractional part of the decimal value, followed by step 2.
- The binary number is found for some significant digits.
Solved Example
Let’s convert 29.188 in binary to 5 significant digits. We have already converted 29 to binary above. Let’s work on the fractional part.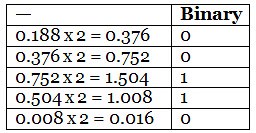
We have reached 5 significant digits. So we stop here. So 43.18810=101011.001102
Decimal to Octal
By repeatedly dividing a number by 8 and recording the result, decimal values can be transformed into octal. Steps to be followed:
Conversion of Integer Decimal Numbers to Octal
- Divide the number by 2.
- Get the integer quotient for the next iteration.
- Get the remainder for the octal digit.
- Repeat the above steps until the quotient is equal to 0.
Solved Example
We read the reminder in reverse order. So 4310=538
Next is the conversion of the fraction part.
Note: The dividend (here given decimal number) is the number to be divided, the divisor (here base of octal, i.e., 8) is the number to be divided by, and the quotient (remaining divided decimal number) is the outcome of the division.
Conversion of Fractional Decimal Numbers to Octal
If the decimal fractional component is M, multiply it by 8 because the octal number system’s base is 8. For the fractional part, follow the steps below:
- Multiply 8 by the fractional part of the decimal number.
- The whole part of the product is our octal equivalent.
- Step 1 is repeated using only the fractional part of the decimal value, followed by step 2.
- The octal number is found for some significant digits.
Solved Example
Let’s convert 43.188 in Octal to 5 significant digits. We have already converted 43 to octal above. Let’s work on the fractional part.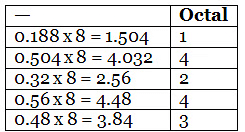
We have reached 5 significant digits. So we stop here. So 4310=53.142438
Decimal to Hexadecimal
By repeatedly dividing a number by 16 and recording the result, decimal values can be transformed into hexadecimal. Steps to be followed:
Conversion of Integer Decimal Numbers to Hexadecimal
- Divide the number by 16.
- Get the integer quotient for the next iteration.
- Get the remainder for the hexadecimal digit.
- Repeat the above steps until the quotient is equal to 0.
Solved Example
Let’s convert 765 to Hexadecimal
We repeatedly divide 765 by 16 till we get 0 reminders.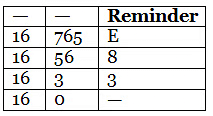
We read the reminder in reverse order. So 76510=38E2
Next is the conversion of the fraction part.
Conversion of Fractional Decimal Numbers to Hexadecimal
If the decimal fractional component is M, multiply it by 16 because the hexadecimal number system’s base is 16. For the fractional part, follow the steps below:
- Multiply 16 by the fractional part of the decimal number.
- The whole part of the product is our hexadecimal equivalent.
- Step 1 is repeated using only the fractional part of the decimal value, followed by step 2.
- The hexadecimal number is found for some significant digits.
Solved Example
Let’s convert 765.565 in Hexadecimal to 5 significant digits. We have already converted 765 to Hexadecimal above. Let’s work on the fractional part.
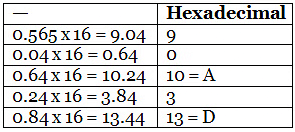
We have reached 5 significant digits. So we stop here. So 765.56510=90A3D2
Binary to Decimal Conversion
To convert a binary number to a decimal number, follow the steps below:
- Count the number of digits in the binary number.
- Starting from the left start multiply the first digit of the binary number by 2 raised to the power of the number of digits.
- Decrease the exponent as you move to the left.
- Add all the digits together.
Here’s the general formula to convert a binary number to a decimal number.
decimal=bn×2n+bn−1×2n−1+bn−2×2n−2+…
Solved Example
Let’s convert 1110012 to decimal.
1110012=1×25+1×24+1×23+0×22+0×21+1×20=5710
Binary to Hexadecimal Conversion
There is no direct method to convert Binary to Hexadecimal. We first convert the binary number to decimal and then convert the decimal number to binary by using the steps we learned above.
The second method to convert Binary to Hexadecimal is by grouping the numbers in a series of 4 from left to right and using the conversion table to convert them to hexadecimal.
Solved Example
Let’s convert (11111111)2 to hexadecimal.
=(11111111)2
=(1111)(1111)=(1111)(1111)
=(15)(15)
=(ff)16
Binary to Octal Conversion
Just like binary to hexadecimal conversion, there is no direct method to convert from binary to octal. We again rely on binary to decimal and decimal to octal. Both of these methods have been already discussed.
The second method is the grouping method. Much like we did in the case of hexadecimal we group the binary numbers in a series of three from left to right. Then we use the conversion chart to convert it into an octal number.
Solved Example
Let’s convert (101010101)2(101010101)2 to octal
=(101010101)2
=(101)(010)(101)
=(525)8
Octal to Decimal Conversion
To convert a number from octal to decimal, follow these steps:
- Count the number of digits.
- Starting from the left multiply the octal number by 8 raised to the power of the number of digits in the octal number.
- Decrease the exponent as you move to the left.
- Add all the digits together.
Here’s the general formula to convert an octal number to a decimal number.
decimal=on×8n+on−1×8n−1+on−2×8n−2+…
Solved Example
Let’s convert 165128 to decimal.
165128=1×84+6×83+5×82+1×81+0×80=7498
Octal to Binary Conversion
It takes two steps to convert an octal number to a binary number. We must first convert the given octal number to its decimal counterpart, then convert the decimal to binary. We have already learnt about those processes.
Octal to Hexadecimal Conversion
We can convert octal to hexadecimal by two indirect methods. The first method involves converting the octal number to a decimal number and then we convert the decimal number to hexadecimal. The second is to convert the octal number to binary and then convert it to hexadecimal. Since there is no direct method to convert octal to binary we avoid the second method. Both of these methods are discussed in the sections above.
Hexadecimal to Decimal Conversion
To convert a number from hexadecimal to decimal, follow these steps:
- Count the number of digits.
- Convert the alphabets into equivalent numbers as shown in the Number System Table above.
- Starting from the left multiply the hexadecimal number by 16 raised to the power of the number of digits in the hexadecimal number.
- Decrease the exponent as you move to the left.
- Add all the digits together.
Here’s the general formula to convert an octal number to a decimal number.
decimal=hn×16n+hn−1×16n−1+hn−2×16n−2+…
Solved Example
Let’s convert A37E16 to decimal.
A37E16=A×163+3×162+7×161+E×160
A37E16=10×163+3×162+7×161+14×160
=41854
Hexadecimal to Binary Conversion
To convert the hexadecimal number into binary no direct method exists. We use the intermediate of the decimal number system by converting hexadecimal to decimal as shown above and then converting the decimal to binary as discussed in previous sections.
Hexadecimal to Octal Conversion
We again do not have a direct method to convert from hexadecimal to octal and resolve to the use of decimal system by converting hexadecimal to decimal as shown above and then convert the decimal to octal as discussed in previous sections.
Solved Examples on Number System
Here are some solved examples on number system to help you practice.
Solved Example 1: Convert 43.01 to binary till 7 significant digits.
Solution: First lets consider the whole number part. We repeatedly divide 43 by 2 till we get 0 remainder.

Now for the fractional part of .01 we start multiplying it by 2.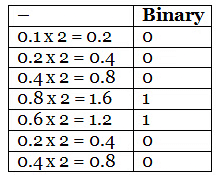
So 43.0110=101011.00011002
Solved Example 2: Convert 473.05 to binary till 5 significant digits.
Solution:
First let’s consider the whole number part. We repeatedly divide 473 by 8 till we get a quotient of 0.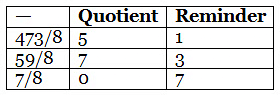
Now for the fractional part of .05 we start multiplying it by 8.
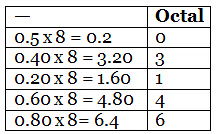
So 473.0510=731.031462
|
49 videos|179 docs|73 tests
|
FAQs on Overview: Number System - Quantitative Techniques for CLAT
| 1. What is a number system and why is it important? |  |
| 2. What are the different types of number systems? |  |
| 3. How did number systems evolve throughout history? |  |
| 4. What is the significance of the base in a number system? |  |
| 5. How do we convert numbers between different number systems? |  |





















