Packing Efficiency & Imperfections in Solids | Chemistry Class 12 - NEET PDF Download
Close Packing of Spheres
Atoms are space-filling entities and structures can be described as resulting from the packing of spheres. The most efficient, called Closest Packing, can be achieved in two ways, one of which is called Hexagonal Close Packing (Hexagonal Primitive) and the other, Cubic Close Packing (ccp or fcc). Hexagonal close-packing can be built up as follows:
Place a sphere on a flat surface. Surround it with six equal spheres as close as possible in the same plane. Looking down on the plane. Let us call this layer as the A layer.
Now form over the first layer a second layer of equally bunched spheres, so as to nestle into the voids. It will be clearly seen that once a sphere is placed over a void, it blocks the void which is adjacent to that void. Let us call this layer as the B layer. Now, it can be clearly seen that there are two types of voids created by the B layer of spheres.
If a sphere is placed on the x - type of voids, it would resemble the A layer of spheres in the sense that it eclipses the spheres of the A layer. This arrangement (i.e., ABAB……) is called the hexagonal close packing (hcp) or hexagonal primitive. On the other hand, if the spheres were to be placed on the y - type of voids, it would neither eclipse the A layer nor the B layer of spheres. This would clearly be a unique layer. Let us call this layer as the C layer. This arrangement (i.e, ABCABC...) is called the Cubic Close Packing (fcc).
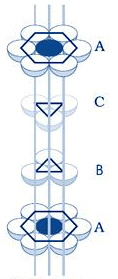
cubic close packing
Exercise 1: It can be seen now that both fcc and Hexagonal Primitive Structure have the same packing fraction. Moreover, this is also the highest packing fraction of all the possible unit cells with one type of atom with empty voids. Can you explain this?
Octahedral and Tetrahedral Voids
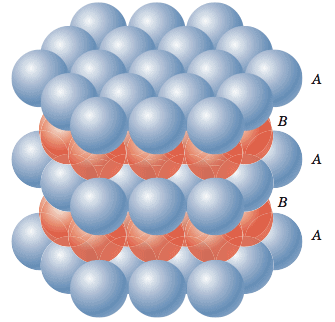
The close packing system involves two kinds of voids - tetrahedral voids and octahedral voids. The former has four spheres adjacent to it while the latter has six spheres adjacent to it. These voids are only found in either fcc or Hexagonal Primitive unit cells. Let us first consider an fcc unit cell. Not all the atoms of the unit cell are shown (for convenience). Let us assume that there is an atom (different from the one that forms the fcc) at the center of an edge.
Let it be big enough to touch one of the corner atoms of the fcc. In that case, it can be easily understood that it would also touch six other atoms (as shown) at the same distance. Such voids in an fcc unit cell in which if we place an atom it would be in contact with six spheres at equal distance (in the form of an octahedron) are called octahedral voids.
On calculation, it can be found out that an fcc unit cell has four octahedral voids effectively.
The number of effective octahedral voids in a unit cell is equal to the effective number of atoms in the unit cell.
Let us again consider an fcc unit cell. If we assume that one of its corners is an origin, we can locate a point having coordinates (¼,¼,¼). If we place an atom (different from the ones that form the fcc) at this point and if it is big enough to touch the corner atom, then it would also touch three other atoms which are at the face centers of all those faces which meet at that corner. Moreover, it would touch all these atoms at the corners of a regular tetrahedron. Such voids are called tetrahedral voids.
Since there are eight corners, there are eight tetrahedral voids in a fcc unit cell. We can see the tetrahedral voids in another way. Let us assume that eight cubes of the same size make a bigger cube. Then the centers of these eight small cubes would behave as tetrahedral voids for the bigger cube (if it were face-centered). The number of tetrahedral voids is double the number of octahedral voids. Therefore, the number of tetrahedral voids in hcp is 12.
Radius Ratio Rules
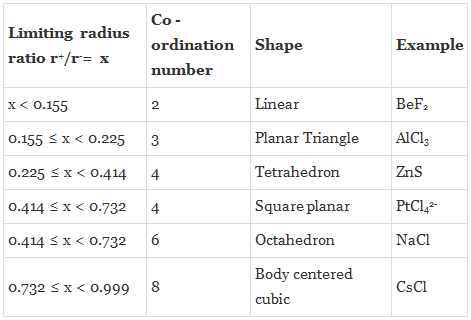
The structure of many ionic solids can be accounted for by considering the relative sizes of the positive and negative ions, and their relative numbers. Simple geometric calculations allow us to work out, as to how many ions of a given size can be in contact with a smaller ion. Thus, we can predict the coordination number from the relative sizes of the ions.
Coordination Number 3
The smaller positive ion of radius r+ is in contact with three larger negative ions of radii r-. It can be seen that AB = BC = AC = 2r-, BD = r- + r+. Further, the angle ABC is 60o, and the angle DBE is 30o.
By trigonometry Cos 30o = (BE / BD). BD = (BE/Cos 30o), r+ + r- = r- /Cos 30o = (r- / 0.866) = r- ´ 1.155, r+ = (1.155 r-) - r- = 0.155 r-,
Hence (r+ / r-) = 0.155.

Coordination Number 4 (Tetrahedron)
Angle ABC is the tetrahedral angle of 109o 28' and hence the angle ABD is half of this, that is 54o44'. In the triangle ABD, Sin ABD = 0.8164 = AD/AB = .
Taking reciprocals,  , rearranging, we get,
, rearranging, we get,  .
.
Coordination Number 6 (Octahedron) or 4 ( Square Planar)
A cross-section through an octahedral site is shown in the adjacent figure and the smaller positive ion (of radius r+) touches six larger negative ions (of radius r-). (Note that only four negative ions are shown in this section and one is above and one below the plane of the paper). It is obvious that AB = r+ + r- and BD = r-. The angle ABC is 45o in the triangle ABD. cos ABD = 0.7071
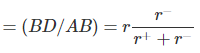
Rearranging, we get, r+/r= 0.414
Exercise 2: The radius of a calcium ion is 94 pm and of an oxide ion is 146 pm. Predict the crystal structure of calcium oxide.
Classification of Ionic Structures
In the following structures, a black circle would denote a cation and a white circle would denote an anion.In any solid of the type AxBy, the ratio of the coordination number of A to that of B would be y: x.
Rock Salt Structure
Cl- is forming an fcc unit cell in which Na+ is in the octahedral voids. The coordination number of Na+ is 6 and therefore that of Cl- would also be 6. Moreover, there are 4 Na+ ions and 4 Cl- ions per unit cell. The formula is Na4Cl4 i.e,NaCl. The other substances having this kind of a structure are halides of all alkali metals except cesium halides and oxides of all alkaline earth metals except beryllium oxide.

Unit cell structure of NaCl
Zinc Blende Structure
Sulfide ions are face centered and Zinc is present in alternate tetrahedral voids. Formula is Zn4S4, i.e, ZnS. Coordination number of Zn is 4 and that of sulfide is also 4. Other substance that exists in this kind of a structure is BeO.
Fluorite Structures
Calcium ions are face-centered and fluoride ions are present in all the tetrahedral voids. There are four calcium ions and eight fluoride ions per unit cell. Therefore the formula is Ca4F8, (i.e, CaF2). The coordination number of fluoride ions is four (tetrahedral voids) and thus the coordination number of calcium ions is eight. Other substances which exist in this kind of structure are UO2, and ThO2.
Anti-Fluorite Structure
Oxide ions are face-centered and lithium ions are present in all the tetrahedral voids. There are four oxide ions and eight lithium ions per unit cell. As it can be seen, this unit cell is just the reverse of Fluorite structure, in the sense that, the positions of cations and anions is interchanged. Other substances which exist in this kind of a structure are Na2O, K2O and Rb2O.
Cesium Halide Structure
Chloride ions are primitive cubic while the cesium ion occupies the center of the unit cell. There is one chloride ion and one cesium ion per unit cell. Therefore the formula is CsCl. The coordination number of cesium is eight and that of chloride ions is also eight. Other substances which exist in this kind of a structure are all halides of cesium.
Corundum Structure
The general formula of compounds crystallizing in corundum structure is A2O3. The closest packing is that of anions (oxide) in hexagonal primitive lattice and two-thirds of the octahedral voids are filled with trivalent cations. Examples are Fe2O3, Al2O3 and Cr2O3.
Perovskite Structure
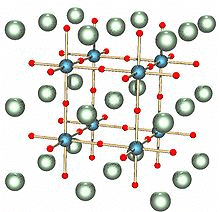
The general formula is ABO3. One of the cations is bivalent and tetravalent. Example: CaTiO3, BaTiO3. The bivalent ions are present in primitive cubic lattice with oxide ions on the centers of all the six square faces. The tetravalent cation is in the center of the unit cell occupying octahedral void.
Spinel and Inverse Spinel Structure
Spinel is a mineral (MgAl2O4). Generally they can be represented as M2+M23+O4 , where M2+ is present in one-eighth of tetrahedral voids in a FCC lattice of oxide ions and M3+ ions are present in half of the octahedral voids. M2+ is usually Mg, Fe, Co, Ni, Zn and Mn; M3+ is generally Al, Fe, Mn, Cr and Rh. Examples are ZnAl2O4, Fe3O4, FeCr2O4 etc.
Many substances of the type  also have this structure. In an inverse spinel the ccp is of oxide ions, M2+ is in one-eight of the tetrahedral voids while M3+ would be in one-eight of the tetrahedral voids and one-fourth of the octahedral voids.
also have this structure. In an inverse spinel the ccp is of oxide ions, M2+ is in one-eight of the tetrahedral voids while M3+ would be in one-eight of the tetrahedral voids and one-fourth of the octahedral voids.
Exercise 3: The unit cell of silver iodide (AgI) has 4 iodine atoms in it. How many silver atoms must be there in the unit cell?
Exercise 4: The coordination number of the barium ions, Ba2+, in barium chloride (BaF2) is 8. What must be the coordination number of the fluoride ions, F-.
Imperfections in a Crystal
The discovery of imperfections in an otherwise ideally perfect crystal is one of the most fascinating aspects of solid state science. An ideally perfect crystal is one which has the same unit cell and contains the same lattice points throughout the crystal.
The term imperfection or defect is generally used to describe any deviation of the ideally perfect crystal from the periodic arrangement of its constituents.
Point Defect
If the deviation occurs because of missing atoms, displaced atoms or extra atoms, the imperfection is named as a point defect. Such defects can be the result of imperfect packing during the original crystallisation or they may arise from thermal vibrations of atoms at elevated temperatures because with increase in thermal energy there is increased probability of individual atoms jumping out of their positions of lowest energy.
The most common point defects are the Schottky defect and the Frenkel defect. Comparatively less common point defects are the metal excess defect and metal deficiency defects. All these defects have been discussed below in some detail.
Schottky Defects: The defects arise if some of the lattice points in a crystal are unoccupied. The points which are unoccupied are called lattice vacancies. The existence of two vacancies, one due to a missing Na+ ion and the other due to a missing Cl ion in a crystal of NaCl, is shown in figure 16. The crystal, as a whole remains neutral because the number of missing positive and negative ions are the same.

Schottky defects appear generally in ionic crystals in which the positive and the negative ions do not differ much in size. Sodium chloride and cesium chloride furnish good examples of ionic crystals in which Schottky defects occurs.
Frenkel Defects:
These defects arise when an ion occupies an interstitial position between the lattice points. This is shown in figure for the crystal of AgBr.
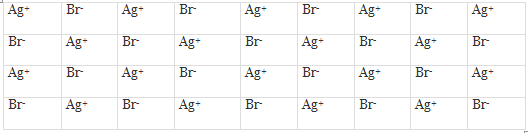
Frenkel Defects in a Crystal
As can be seen, one of the Ag+ ions occupies a position in the interstitial space rather than its own appropriate site in the lattice. A vacancy is thus created in the lattice as shown. It may be noted again that the crystal remains neutral since the number of positive ions is the same as the number of negative ions. The presence of Ag+ ions in the interstitial space of AgBr crystal is responsible for the formation of a photographic image on the exposure of AgBr crystals (i.e., photographic plate) to light.
ZnS is another crystal in which Frenkel defects appear. Zn2+ ions are entrapped in the interstitial space leaving vacancies in the lattice.
Frenkel defects appear in crystals in which the negative ions are much larger than the positive ions. Like Schottky defects, the Frenkel defects are also responsible for the conduction of electricity in crystals and also for the phenomenon of diffusion in solids.
Metal Excess Defects(The Colour Centres) It has been observed that if a crystal of NaCl is heated in sodium vapour, it acquires a yellow colour.
This yellow colour is due to the formation of a non-stoichiometric compound of sodium chloride in which there is a slight excess of sodium ions. What happens in this case is that some sodium metal gets doped into sodium chloride crystal which, due to the crystal energy, gets ionised into Na+ and Cl-. This electron occupies a site that would otherwise be filled by a chloride ion, as illustrated in the figure.
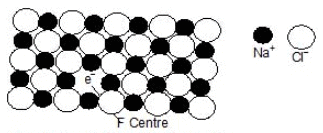
F-centre in a Sodium chloride crystal
There is evidently an excess of metal ions although the crystal as a whole is neutral. A little reflection would show that there are six Na+ sites adjacent to the vacant site occupied by the electron. The extra electron in thus shared between all the six Na+ ions which implies that this electron is not localised at the vacant Cl site. On the other hand, this electron is similar to the delocalised p electrons present in molecules containing conjugated double bonds.
Light is absorbed when this delocalised electron makes an easy transition from its ground state to an excited state. As a result, the non-stoichiometric form of sodium chloride appears coloured. Because of this, the sites occupied by the extra electrons are known as colour centers. These are also called F-centres. This name comes from the German word Farbe meaning colour. The non-stoichiometric sodium chloride may be represented by the formula Na(1+d)Cl where d is the excess sodium metal doped in the crystal because of its exposure to sodium vapour.
Another common example of metal excess defects is the formation of a magenta coloured non-stoichiometric compound of potassium chloride by exposing the crystals of KCl to K metal vapour. The coloured compound contains an excess of K+ ions, the vacant Cl sites being filled by electrons obtained by the ionization of the excess K metal-doped into the crystal.
Metal Deficiency Defects.
In certain cases, one of the positive ions is missing from its lattice site and the extra negative charge is balanced by some nearby metal ion acquiring two charges instead of one. There is evidently, a deficiency of the metal ions, although the crystal as a whole is neutral.
This type of defect is generally found amongst the compounds of transition metals which can exhibit variable valency. Crystals of FeO, FeS and NiO show this type of defects. The existence of metal deficiency defects in the crystal of FeO is illustrated.
 It is evident from the above discussion that all types of point defects result in the creation of vacancies or `holes' in the lattice of the crystals. The presence of holes lowers the density as well as the lattice energy or the stability of the crystals. The presence of too many holes may cause a partial collapse of the lattice.
It is evident from the above discussion that all types of point defects result in the creation of vacancies or `holes' in the lattice of the crystals. The presence of holes lowers the density as well as the lattice energy or the stability of the crystals. The presence of too many holes may cause a partial collapse of the lattice.
|
108 videos|286 docs|123 tests
|
FAQs on Packing Efficiency & Imperfections in Solids - Chemistry Class 12 - NEET
| 1. How do you define packing efficiency in solids? |  |
| 2. What factors affect the packing efficiency of solids? |  |
| 3. How does packing efficiency relate to the physical properties of solids? |  |
| 4. What are some common imperfections in solid structures? |  |
| 5. How do imperfections in solids affect their properties? |  |

|
Explore Courses for NEET exam
|

|


















