Year 11 Exam > Year 11 Notes > Mathematics for GCSE/IGCSE > Parallel & Perpendicular Lines
Parallel & Perpendicular Lines | Mathematics for GCSE/IGCSE - Year 11 PDF Download
Parallel Lines
What are parallel lines?
- Parallel lines share the same slope but are distinct from one another.
- Parallel lines never intersect.
- When lines are expressed in the form y = mx + c, you can easily identify parallel lines by their identical 𝑚m values (slopes).
- For example, y = 3x + 7 and y = 3x − 4 are parallel because they have the same slope.
- In contrast, y = 2x + 3 and y = 3x + 3 are not parallel since their slopes are different.
- Although y = 4x + 9 and y = 4x + 9 have the same slope, they are not parallel because they represent the same line.
How do I find the equation of a line parallel to another line?
- Since parallel lines have the same slope, a line in the form y = mx + c will be parallel to a line in the form y = mx + d, with the same 𝑚m for both lines.
- If c = d, then the lines would be identical and not parallel.
- To find the equation of a line parallel to y = mx + c, you will need information about a point (x1, y1) that the parallel line y = mx + d passes through.
- Substitute the point (x1, y1) into y = mx + d and solve for d.
Perpendicular Lines
- It is a known fact that parallel lines have equal gradients.
- Perpendicular lines intersect each other at right angles, specifically at 90°.
What’s the deal with perpendicular gradients (and lines)?
- Before delving into perpendicular gradients and lines, it's crucial to grasp how to determine the equation of a straight line. This skill will be fundamental for solving related problems.
- Gradients m1 and m2 are considered perpendicular if m1 x m2 = -1.
- For instance,
- 1 and −1
- 1/3 and 3
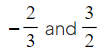
- We can use m2 = −1 ÷ m1 to find a perpendicular gradient. This is called the negative reciprocal.
- When in doubt, sketching the lines can provide a visual aid in understanding the perpendicular relationship between two gradients.
The document Parallel & Perpendicular Lines | Mathematics for GCSE/IGCSE - Year 11 is a part of the Year 11 Course Mathematics for GCSE/IGCSE.
All you need of Year 11 at this link: Year 11
|
84 videos|120 docs
|
FAQs on Parallel & Perpendicular Lines - Mathematics for GCSE/IGCSE - Year 11
| 1. How can we determine if two lines are parallel using their equations? |  |
Ans. Two lines are parallel if their slopes are equal. This means that if the gradients of the lines are the same, then the lines are parallel.
| 2. Can two perpendicular lines have the same slope? | |
Ans. No, perpendicular lines have slopes that are negative reciprocals of each other. This means that if one line has a slope of m, the perpendicular line will have a slope of -1/m.
| 3. How can we find the equation of a line that is perpendicular to a given line passing through a specific point? | |
Ans. To find the equation of a line perpendicular to a given line, first find the negative reciprocal of the slope of the given line. Then, use the point-slope form of the equation to find the equation of the perpendicular line passing through the given point.
| 4. Can two lines be both parallel and perpendicular to each other at the same time? | |
Ans. No, two lines cannot be both parallel and perpendicular to each other at the same time. If two lines are parallel, they will never intersect, while perpendicular lines intersect at a right angle.
| 5. How can we determine if two lines are perpendicular by looking at their equations? | |
Ans. Two lines are perpendicular if the product of their slopes is -1. This means that if the gradients of the lines are m1 and m2, then m1 * m2 = -1, indicating that the lines are perpendicular.
Related Exams
About this Document
|
Nov 22, 2024 Last updated |
Document Description: Parallel & Perpendicular Lines for Year 11 2024 is part of Mathematics for GCSE/IGCSE preparation.
The notes and questions for Parallel & Perpendicular Lines have been prepared according to the Year 11 exam syllabus. Information about Parallel & Perpendicular Lines covers topics
like Parallel Lines, Perpendicular Lines and Parallel & Perpendicular Lines Example, for Year 11 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Parallel & Perpendicular Lines.
Introduction of Parallel & Perpendicular Lines in English is available as part of our Mathematics for GCSE/IGCSE
for Year 11 & Parallel & Perpendicular Lines in Hindi for Mathematics for GCSE/IGCSE course.
Download more important topics related with notes, lectures and mock test series for Year 11
Exam by signing up for free. Year 11: Parallel & Perpendicular Lines | Mathematics for GCSE/IGCSE - Year 11
Description
Full syllabus notes, lecture & questions for Parallel & Perpendicular Lines | Mathematics for GCSE/IGCSE - Year 11 - Year 11 | Plus excerises question with solution to help you revise complete syllabus for Mathematics for GCSE/IGCSE | Best notes, free PDF download
Information about Parallel & Perpendicular Lines
In this doc you can find the meaning of Parallel & Perpendicular Lines defined & explained in the simplest way possible. Besides explaining types of
Parallel & Perpendicular Lines theory, EduRev gives you an ample number of questions to practice Parallel & Perpendicular Lines tests, examples and also practice Year 11
tests
|
Explore Courses for Year 11 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
practice quizzes
,video lectures
,Summary
,Objective type Questions
,Parallel & Perpendicular Lines | Mathematics for GCSE/IGCSE - Year 11
,Parallel & Perpendicular Lines | Mathematics for GCSE/IGCSE - Year 11
,Semester Notes
,Exam
,past year papers
,Extra Questions
,Previous Year Questions with Solutions
,mock tests for examination
,study material
,Important questions
,Viva Questions
,MCQs
,ppt
,Parallel & Perpendicular Lines | Mathematics for GCSE/IGCSE - Year 11
,Sample Paper
,Free
,shortcuts and tricks
;
Additional Information about Parallel & Perpendicular Lines for Year 11 Preparation
Parallel & Perpendicular Lines Free PDF Download
The Parallel & Perpendicular Lines is an invaluable resource that delves deep into the core of the Year 11 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Parallel & Perpendicular Lines now and kickstart your journey towards success in the Year 11 exam.
Importance of Parallel & Perpendicular Lines
The importance of Parallel & Perpendicular Lines cannot be overstated, especially for Year 11 aspirants.
This document holds the key to success in the Year 11 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Parallel & Perpendicular Lines Notes
Parallel & Perpendicular Lines Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Parallel & Perpendicular Lines.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Parallel & Perpendicular Lines Notes on EduRev are your ultimate resource for success.
Parallel & Perpendicular Lines Year 11 Questions
The "Parallel & Perpendicular Lines Year 11 Questions" guide is a valuable resource for all aspiring students preparing for the
Year 11 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Parallel & Perpendicular Lines on the App
Students of Year 11 can study Parallel & Perpendicular Lines alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Parallel & Perpendicular Lines,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Parallel & Perpendicular Lines is prepared as per the latest Year 11 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup