Portfolio Theory | Management Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Key Concepts of the Markowitz Model |

|
| The Conceptual Framework |

|
| Prospect Theory |

|
Introduction
- In the realm of financial markets, various portfolio investment theories have provided investors with numerous criteria for selecting the most suitable portfolio. These theories, each grounded in distinct assumptions, prioritize addressing investor needs and preferences. Among these theories, one of the most renowned is proposed by Harry M. Markowitz, commonly referred to as the Markowitz model.
- This model has gained prominence for its introduction of novel risk measurement concepts and their application in constructing diverse portfolios for investors. Based on the assumption that the typical investor's attitude towards risk is characterized by risk aversion, the model aims to maximize portfolio expected returns while minimizing risk. Furthermore, this unit will delve into investor behavior as elucidated by Prospect Theory and the underlying rationales behind such behavior as elucidated by behavioral economics.
Key Concepts of the Markowitz Model
- The Markowitz model stands as a prominent tool for comprehending and assessing the intricate relationship between risk and return within investments. It furnishes a theoretical framework essential for evaluating portfolio risk and return, offering valuable insights for capital budgeting and related decisions. This model has significantly influenced portfolio theory in two significant ways. Firstly, it employs statistical methodologies to gauge risk in portfolio analysis. Secondly, it utilizes mathematical programming techniques to identify the most efficient portfolio for investors. The framework of the model has introduced the notion of efficient portfolios into portfolio management. An efficient portfolio is characterized as one that provides the highest return to investors for a given level of risk. In simpler terms, an efficient portfolio is one that yields maximum returns at the lowest possible risk for the expected level of return.
- The model selects efficient portfolios based on a specified amount of investor wealth and generates a range of portfolios tailored to individual risk and return preferences. Each investor possesses distinct levels of wealth, risk tolerance, and asset preferences. Furthermore, individual expectations regarding investment returns, expenses, and investment needs vary considerably. Consequently, a multitude of portfolios are created to accommodate diverse investor needs, each necessitating separate evaluation to ascertain efficiency.
- The process entails identifying the optimal combination of securities that align with the investor's preferences, aligning with their investment objectives and requirements. In portfolio theory, the decision-making process for individual assets differs significantly from that for a portfolio. This divergence arises from the fact that the quality of a portfolio is distinct from the quality of individual asset components. The risk associated with the combination of two assets within a portfolio differs from the combined risk of the individual assets themselves.
- The two primary attributes evaluated by investors in every investment are risk and reward. Risk, as assessed by investors, is measured through the variance of the distribution around the mean, commonly referred to as the portfolio variance. The relationship between asset movements is defined by covariance. The Markowitz model optimizes returns while minimizing risk within the preferred risk-return profile. There exists a positive correlation between risk and return, implying that higher returns necessitate greater risk-taking. However, investors seeking high returns with lower risk can apply the Modern Portfolio Theory, which emphasizes the trade-off between risk and return.
- Before delving into the Markowitz Model, it's essential to revisit the concepts of portfolio investment. A portfolio comprises a combination of assets or securities selected for investment. Each investor diversifies their investment across various assets, ensuring that assets are not perfectly correlated, and portfolio diversification aligns with preferences for wealth, return, and risk. In contrast, the traditional portfolio management theory selects assets based on minimizing risk, measured by the portfolio's standard deviation, with returns solely based on expected mean returns. Investors typically favor assets with stable returns over time to mitigate risk, avoiding assets with high return variability.
- The Modern Portfolio Theory, in contrast, advocates for a combination of securities that maximize returns while minimizing total portfolio variability. Diversification benefits are realized by combining assets where the risk of one offsets that of another. The variability and covariance of returns between securities are crucial considerations, indicating the extent to which diversification benefits investors. Higher covariance and return variability increase portfolio risk, diminishing the benefits of diversification. Therefore, the selection of a portfolio under the Modern Portfolio Theory entails considering expected returns and the variance of these returns, alongside covariance between securities.
- Furthermore, the covariance among the returns of the securities within the portfolio is another crucial factor to consider. Thorough evaluation of these factors is expected to yield an efficient portfolio. Such a portfolio is anticipated to deliver the highest possible return for the lowest level of risk among the various portfolios available to the investor.
The Markowitz theory rests upon several key assumptions, which are as follows:
- Investors exhibit rational behavior, aiming to maximize their utility by seeking the highest possible returns with their given level of income or wealth.
- Investors possess complete information regarding the risk and return characteristics of assets, ensuring access to fair and accurate information on securities' returns and risks.
- Markets operate efficiently, promptly and accurately responding to changes in information.
- Investors exhibit a risk-averse attitude, preferring minimum risk and maximum return.
- Investors base their decisions on expected returns and the variance of returns from the mean.
- Given a certain level of risk, investors opt for the portfolio offering higher returns, reflecting monotonic return preferences.
The Conceptual Framework
- When these assumptions are met, the portfolio of assets selected by the investor is expected to yield an efficient portfolio. In other words, no asset or combination of assets can offer a higher expected return while maintaining the same level of risk or lower risk with the same or higher expected return. Efficient portfolios are achieved through diversification, a process that mitigates unsystematic risk, also known as company-specific risk. Diversification works by offsetting the variability of returns from one company with the stability of returns from another. Complete diversification occurs when there is negative correlation between the returns of the securities considered.
- The components forming a portfolio are referred to as assets or securities. These assets, which are subject to evaluation of their return and risk, can include stocks, currencies, options, bonds, or portfolios. For instance, consider an investor acquiring an asset at the outset, denoted as time zero (t = 0), and subsequently selling it at a later date, marked as time T in the future. This investment scenario typically unfolds within a single period, with no associated tax or transaction costs involved in the purchase and sale of securities in the financial market. Let 𝑋0 represent the initial investment amount at time t = 0, and 𝑋𝑇 denote the maturity amount expected to be received upon expiration at time T. Consequently, the total return on the investment, denoted as R, is defined as the ratio of the maturity amount to the initial investment sum made by the investor. This relationship can be expressed mathematically as:
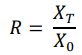
- The rate of return r is calculated as the ratio of the difference in the change in the amount received and invested as the initial investment. This is measured in percentage terms as:
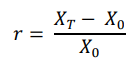
- Hence, the total return of the investment can also be written as
R = 1 + r - The above equation gives the relationship between R and r. We now extend this to assume that there are N different assets available to the investor to choose and each of them has a corresponding total return 𝑅t , i = 1, . . . , N. Now, in order to form a portfolio, the investor has to spread out his amount of investment among these assets to generate a portfolio with different returns (and different weights assigned to each asset). Let us say that the weights are denoted by 𝑤i , i = 1, . . . , N. Let us further assume that an amount invested in an asset i is denoted by 𝑋0i so that the sum of all the investment in different assets is equal to the total investment that an investor wish to invest. That is:
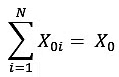 and the amount of investment will be positive i.e. 𝑋0i ≥ 0, i = 1, .., N. Since the weights represents the proportion of the total money invested in that particular asset, the amount of investment in each asset is given by:
and the amount of investment will be positive i.e. 𝑋0i ≥ 0, i = 1, .., N. Since the weights represents the proportion of the total money invested in that particular asset, the amount of investment in each asset is given by:
𝑋0i = 𝑤i𝑋0 - Note that the sum over all weights is equal to one because the total investment R is invested in different assets chosen by the investor. Now, the maturity amount received at the expiration date of the asset at time T of the ith asset is written as 𝑅i 𝑤i 𝑋0 . Hence, the total return R of the portfolio is given by:
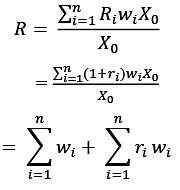
- Since the sum of all 𝑤i is one and R = 1 + r, we can rewrite R in terms of r as:
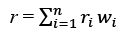
Expected Value and Variance of the Return
- We know that the rate of return on investment is uncertain because the amount received at the time of selling is not known due to the fluctuations in the spot prices of the asset. Thus, r is a random variable which fluctuates depending on the market prices of the respective asset. In order to understand the overall rate of return of an investment, it is therefore better to consider the mean for each of the N assets, denoted by
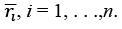
- Let us denote the variance of asset i as
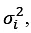 and the covariance between the two assets i.e. assets i and j is given by 𝜎ij . The expected return of a portfolio 𝑟̅ is the product of weight of the asset i and the expected average rate of return on asset i. Symbolically,
and the covariance between the two assets i.e. assets i and j is given by 𝜎ij . The expected return of a portfolio 𝑟̅ is the product of weight of the asset i and the expected average rate of return on asset i. Symbolically,
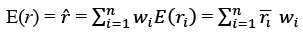
- The variance 𝜎2 of the portfolio return is given by:
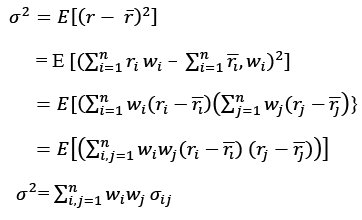
The Model’s Framework
- According to the Markowitz modelling framework, the problem of portfolio selection can be understood and solved in two ways. One way for the investor is to minimize the variance of the portfolio with respect to the expected return 𝑟̅. The other way is to maximize the expected return given a variance of the portfolio. This is known as the Markowitz model.
To express it mathematically, the problem can be formulated as
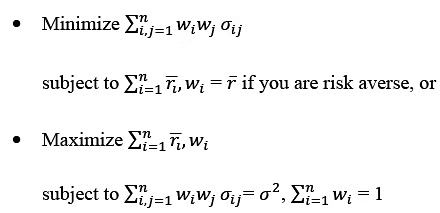
The second is the dual of first one. The solution to the Markowitz model is an optimization problem and can be solved using Lagrange multipliers or linear programming technique.
Prospect Theory
- The major problem in the real life for a decision maker is to take decisions under uncertainty. Investor has to carefully evaluate all the possible course of action and take decision which ultimately decides the fate of the investment. We know the fact that future is uncertain and profit and loss are part of every investment. But every investor has the objective of wealth maximisation which requires weighing profit and loss in every alternative investment available. According to the economic theory, a rational investor would weigh profit and losses equally under risky situations.
- For instance, it has been observed that people buy lottery tickets when the expected value of payoff from the lottery is less than the cost of the lottery. This has been found inconsistent with most common utility functions. Harry Markowitz (1952) answered this concern by proposing a solution in which he suggested that the willingness to gamble depended very much on the status quo of the investor. In other words, the risk attitude of an investor about gambles of varying amounts largely depends on their ―customary wealth” that decides whether they want to invest in a particular gamble or not.
- In consumer utility theories, it's commonly assumed that the utility function of a consumer is concave. However, Markowitz's model suggests that the utility function of an investor is convex at certain points and concave at others. Traditional financial models typically presume investors to be risk-averse and expect their behavior to remain consistent in decision-making under uncertainty.
- However, contrary to traditional views, numerous researchers, including Harry Markowitz, have observed that attitudes towards risk aversion (or risk-seeking) are often inconsistent, largely influenced by how risks are framed and understood by investors. As a result, investors' decisions under risk and uncertainty are impacted by their psychology, mood, and mental shortcuts or heuristics, leading to inconsistencies in their behavior. Consequently, it becomes challenging to observe investor decision-making theories as proposed by traditional models in the real world.
- Drawing from observations and numerous experiments, Kahneman and Tversky formulated Prospect Theory, a model aimed at explaining decisions that deviate from traditional theories, which assume rational probability assessments and standard utility functions in investor decision-making. Similar to the Markowitz utility model, Prospect Theory also noted an asymmetric attitude toward risk in their experiments.
- Under Prospect Theory, the assessment of loss and benefit is tied to a specific reference point, which determines the magnitude of potential gains or losses. This reference point varies from one individual to another, encompassing factors such as an investor's current wealth, their neighbor's wealth, gains from the previous year, inflation rate, or the purchase price of the asset.
- The utility function proposed by Kahneman and Tversky is concave above the chosen reference point and convex below it, reflecting the concept of loss aversion, where losses weigh more heavily on investors' decisions than gains. This utility function, depicting an investor's risk-averse attitude, leads to divergent decisions based on whether outcomes are perceived as gains or losses.
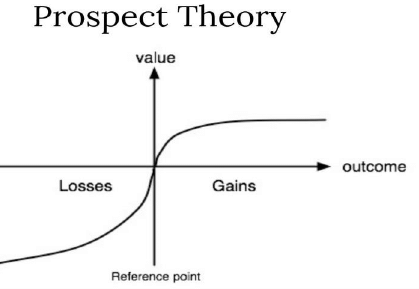
In Figure, the point where the curve intersects the axis signifies a balance between gains and losses. The vertical axis represents the specific reference point against which the function's value is assessed. A shift in the investor's attitude from being risk-loving to risk-averse is marked by an inflection at this intersection point. Below this point, a loss-averse investor is inclined to pursue gains rather than incur losses. Consequently, the investor prefers taking a gamble over facing a potential loss. Prospect Theory has extensively examined this asymmetric approach to risk.
FAQs on Portfolio Theory - Management Optional Notes for UPSC
| 1. What is the Markowitz Model? |  |
| 2. What are the key concepts of the Markowitz Model? |  |
| 3. How does the Markowitz Model relate to the Conceptual Framework? |  |
| 4. What is Prospect Theory? |  |
| 5. How does Portfolio Theory relate to the UPSC exam? |  |














