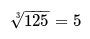Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Powers, Roots & Indices
Powers, Roots & Indices | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Powers & Roots
What are powers/indices?
- Powers of a number involve multiplying that number by itself repeatedly.
- For example,
51 equals 5
52 equals 5 × 5
53 equals 5 × 5 × 5 - The base number is the larger number at the bottom, while the index or exponent is the smaller number raised.
- Any non-zero number to the power of 0 equals 1, as in 50 = 1.
What are roots?
- Roots of a number are the opposite of powers.
- A square root of 25 is a number that, when squared, equals 25. For instance, the square roots of 25 are 5 and -5. Every positive number has two square roots - one positive and one negative.
- The notation √ refers to the positive square root of a number.
- √25 = 5
- To represent both roots simultaneously, we can use the ± symbol.
- Square roots of 25 are ±√25 equals ± 5
- The square root of a negative number is not a real number
- The positive square root can be written as an index of
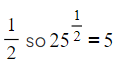
- The notation √ refers to the positive square root of a number.
- A cube root of 125 is a number that when cubed equals 125
- A cube root of 125 is 5
- Every positive and negative number always has a cube root
- The notation∛ refers to the cube root of a number
- The cube root can be written as an index of

- A nth root of a number (n√)is a number that when raised to the power n equals the original number
- If n is even then they work the same way as square roots
- Every positive number will have a positive and negative nth root
- The notation n√ refers to the positive nth root of a number
- If n is odd then they work the same way as cube roots
- Every positive and negative number will have an nth root
- The nth root can be written as an index of 1/n
- If n is even then they work the same way as square roots
- If you know your powers of numbers then you can use them to find roots of numbers
- e.g. 25 equals 32 means 5√ 32 = 2
You could write this using an index
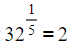
You can also estimate roots by finding the closest powers
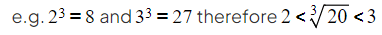
What are reciprocals?
- The reciprocal of a number is the number that you multiply it by to get 1
- The reciprocal of 2 is 1/2
- The reciprocal of 0.25 or 14
- The reciprocal of 3/2 is 2/3
- The reciprocal of a number can be written as a power with an index of -1
- 5-1 means the reciprocal of 5
- This idea can be extended to other negative indices
- 5-2 means the reciprocal of 52
Laws of Indices
What are the laws of indices?
- Numerous fundamental laws or rules exist.
- It's crucial to comprehend and effectively apply these rules.
- Grasping the explanations behind these rules aids in their retention and application.


How do I apply more than one of the laws of indices?
- Powers can include negatives and fractions
- These can be dealt with in any order
- However the following order is easiest as it avoids large numbers
- If there is a negative sign in the power then deal with that first
- Take the reciprocal of the base number
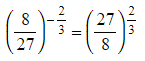
- Next deal with the denominator of the fraction of the power
- Take the root of the base number
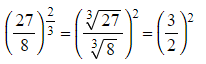
- Finally deal with the numerator of the fraction of the power
- Take the power of the base number
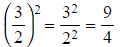
How do I deal with different bases?
- Occasionally, expressions feature various base values.
- Index laws can be utilized to convert the base of a term, simplifying an expression that incorporates terms with differing bases.
- For example
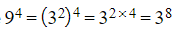
- Using the above can then help with problems like
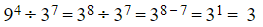
The document Powers, Roots & Indices | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
FAQs on Powers, Roots & Indices - Mathematics for GCSE/IGCSE - Class 10
| 1. What are the basic laws of indices when dealing with powers and roots? |  |
Ans. The basic laws of indices include rules for multiplying, dividing, raising a power to a power, and simplifying expressions with the same base.
| 2. How do you simplify expressions involving powers and roots using the laws of indices? |  |
Ans. To simplify expressions, apply the appropriate laws such as combining like terms, multiplying/dividing powers with the same base, and simplifying radical expressions.
| 3. How can powers and roots be expressed in standard form? |  |
Ans. Powers and roots can be expressed in standard form by writing the number as a decimal between 1 and 10 multiplied by a power of 10.
| 4. Can you provide an example of how to apply the laws of indices to simplify a complex expression? |  |
Ans. Yes, for example, simplifying (2^3 × 2^4) ÷ (2^2) would involve adding the exponents and then dividing to get the final simplified expression.
| 5. What is the significance of understanding powers, roots, and standard form in real-world applications? |  |
Ans. Understanding these concepts is crucial in various fields such as science, engineering, and finance where calculations involving large numbers or scientific notation are common.
Related Searches