Practice Questions: Circles | Mathematics (Maths) Class 10 PDF Download
Q1. Given a right triangle PQR which is right-angled at Q. QR = 12 cm, PQ = 5 cm. The radius of the circle which is inscribed in triangle PQR will be?
 View Answer
View Answer 
Sol: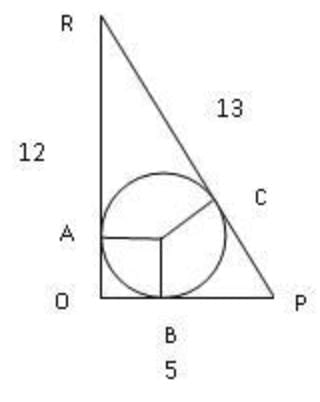
From the diagram:-
RA + AO = 12 ______ (1)
RC + CP = 13 _______ (2)
OB + BP = 5 _______ (3)
Now from the above figure
Side AO = Side OB = Radius of the circle
Side RA = Side RC
Line BP = Line CP
Rewriting these three equations we get
RA + AO = 12 _______ (4)
RA + BP = 13 _______ (5)
AO + BP = 5 _______(6)
(4) – (6) + (5)
RA – BP = 7
RA + BP = 13
2 RA = 20
RA = 10
From equation 4, AO = 12 – 10 = 2 cm
Since AO is equal to radius of the inscribed circle, radius = 2 cm.
Q2. How many tangents can be drawn from the external point to a circle?
 View Answer
View Answer 
Sol: Two tangents can be drawn from the external point to a circle.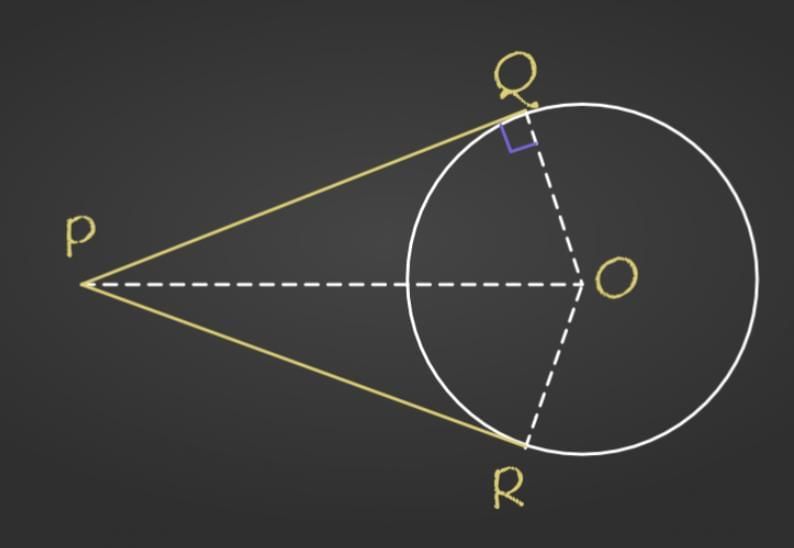
Q3. From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.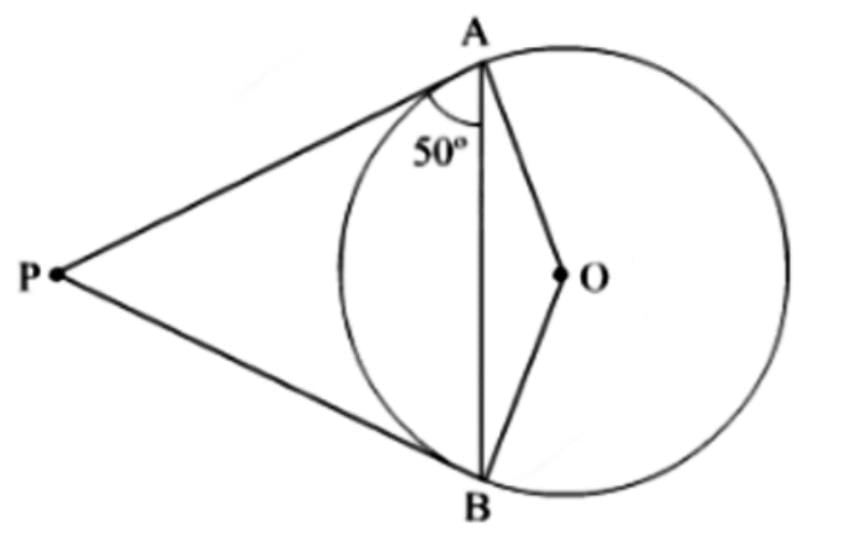
 View Answer
View Answer 
Sol: It is given that PA and PB are tangents to the given circle.
∴ ∠PAO = 90° (Radius is perpendicular to the tangent at the point of contact.)
Now, ∠PAB = 50° (Given)
∴ ∠OAB = ∠PAO − ∠PAB = 90° − 50° = 40°
In △OAB,
OB = OA (Radii of the circle)
∴ ∠OAB = ∠OBA = 40° (Angles opposite to equal sides are equal.)
Now
∠AOB + ∠OAB + ∠OBA = 180° (Angle sum property)
⇒ ∠AOB = 180° − 40° − 40° = 100°
Q4. In given figure, PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA.
 View Answer
View Answer 
Sol: In the given figure,
In △ACO,
OA = OC …(Radii of the same circle)
∴ △ACO is an isosceles triangle.
∠CAB = 30° …(Given)
∴ ∠CAO = ∠ACO = 30°…(angles opposite to equal sides of an isosceles triangle are equal)
∠PCO = 90° …(radius drawn at the point of contact is perpendicular to the tangent)
Now ∠PCA = ∠PCO − ∠CAO
∴ ∠PCA = 90° − 30° = 60°
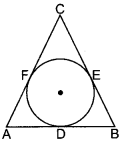
Q5. In given figure, a circle is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF.
 View Answer
View Answer 
Sol: Given that AB = 12 cm, BC = 8 cm and AC = 10 cm.
Let AD = AF = p cm, BD = BE = q cm and CE = CF = r cm ....(Tangents drawn from an external point to the circle are equal in length)
⇒ 2(p + q + r) = AB + BC + AC = AD + DB + BE + EC + AF + FC = 30 cm
⇒ p + q + r = 15
AB = AD + DB = p + q = 12 cm
Therefore, r = CF = 15 - 12 = 3 cm.
AC = AF + FC = p + r = 10 cm
Therefore, q = BE = 15 - 10 = 5 cm.
Therefore, p = AD = p + q + r - r - q = 15 - 3 - 5 = 7 cm.
Q6. From a point P which is at a distance of 13 cm from the centre O of the circle of radius 5 cm, the pair of the tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(a) 60 cm2
(b) 65 cm2
(c) 30 cm2
(d) 32.5 cm2
 View Answer
View Answer 
Sol: From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is 60 cm².
Explanation:
Firstly, draw a circle of radius 5 cm with centre O.
P is a point at a distance of 13 cm from O.
A pair of tangents, PQ and PR, is drawn.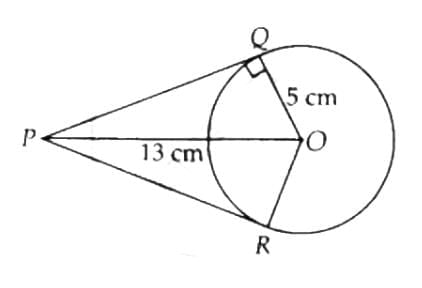
Thus, quadrilateral PQOR is formed.
∴ OQ ⊥ QP ...[Since QP is a tangent line]
In right-angled ΔPQO,
OP² = OQ² + QP²
⇒ 13² = 5² + QP²
⇒ QP² = 169 - 25 = 144
⇒ QP = 12 cm
Now, the area of ΔOQP
= ½ × QP × QO
= ½ × 12 × 5
= 30 cm²
∴ Area of quadrilateral PQOR
= 2 × ar ΔOQP
∴ Area of quadrilateral PQOR
= 2 × ar ΔOQP
= 2 × 30
= 60 cm²
Q7. True/False
When the chord AB makes an angle of 60° at the circle’s centre, the angle between the tangents on A and B is at 60°.
 View Answer
View Answer 
Sol: False
Explanation: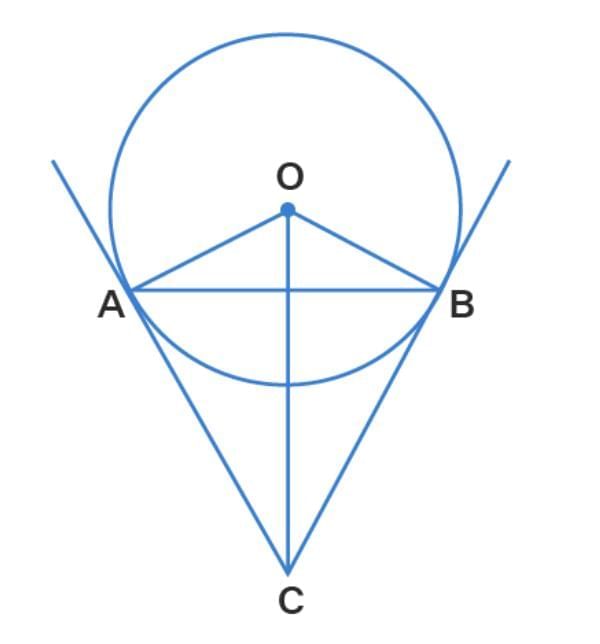
As tangent to any point on the circle is perpendicular to the radius through the point of contact,
OA ⏊ AC and OB ⏊ CB
∠OBC = ∠OAC = 90° …(1)
Using angle sum property of quadrilateral in Quadrilateral AOBC,
∠OBC + ∠OAC + ∠AOB + ∠ACB = 360°
Substituting the values
90° + 90° + 60° + ∠ACB = 360°
So we get
∠ACB = 120°
Angle between two tangents is 120°.
Therefore, the statement is false.
Q8. The length of the tangent for the external point on the circle is always greater than the circle’s radius.
 View Answer
View Answer 
Sol: False
Explanation: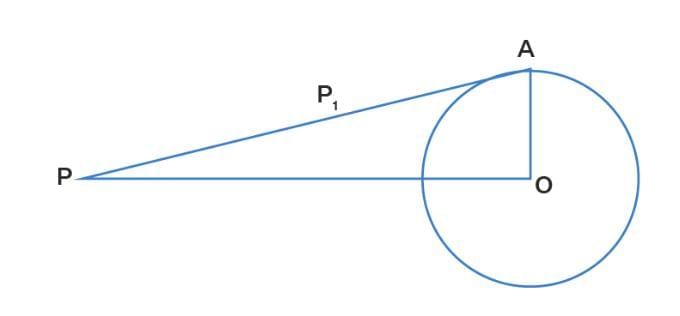
Let P be a point external to the circle away from O
Construct a tangent PA on the circle
PA > r
Now, let us consider a point P1 on the tangent AP near to contact point A of tangent
PA, P1A < AO
The length of tangent PA and P1A are greater and smaller than the radius OA
So the length of tangent may or may not be greater than the radius
Therefore, the statement is false.
Q9. Fill in the blanks:
(i) A tangent to the circle cuts it in _______________ point(s).
(ii) A line intersecting the circle in two points is called a ___________________.
(iii) A circle could have _____________________ parallel tangents at the most.
(iv) The common point of the tangent to the circle and the circle is called ________________________.
 View Answer
View Answer 
Sol: (i) A tangent to the circle cuts it into one point(s).
(ii) A line intersecting the circle in two points is called a secant.
(iii) A circle could have two parallel tangents at the most.
(iv) The common point of the tangent to the circle and the circle is called the point of contact.
Q10. A tangent PQ at the point P of the circle of radius 5 cm meets the line passing through the centre O at the point Q such that OQ = 12 cm. What will be the length of PQ?
 View Answer
View Answer 
Sol: 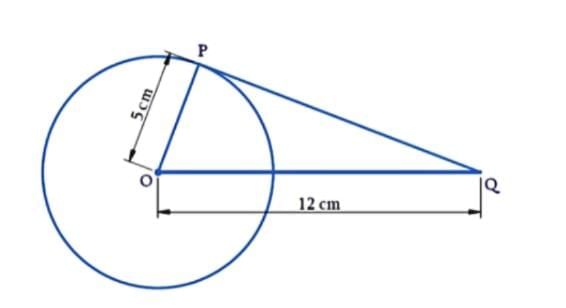 We have to find the length of the tangent PQ.
We have to find the length of the tangent PQ.
ΔOPQ is a right-angle triangle according to Theorem 10.1: The tangent at any point of a circle is perpendicular to the radius through the point of contact.
By Pythagoras theorem:
OQ² = OP² + PQ²
12² = 5² + PQ²
144 = 25 + PQ²
PQ² = 119
PQ = √119
Thus, the length of PQ is √119 cm.
Q11. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°, then ∠ POA is equal to?
 View Answer
View Answer 
Sol: Let's draw a figure as per the question.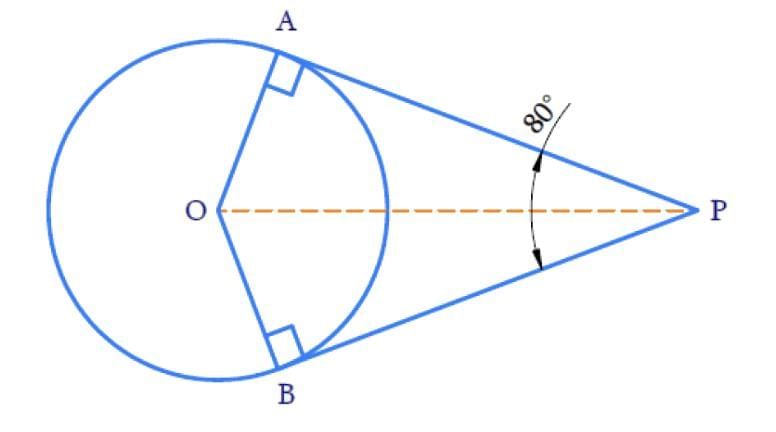
The lengths of tangents drawn from an external point to a circle are equal.
A tangent at any point of a circle is perpendicular to the radius at the point of contact.
In ΔOAP and in ΔOBP
OA = OB (radii of the circle are always equal)
AP = BP (length of the tangents)
OP = OP (common)
Therefore, by SSS congruency ΔOAP ≅ ΔOBP
SSS congruence rule: If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
If two triangles are congruent then their corresponding parts are equal.
Hence,
∠POA = ∠POB
∠OPA = ∠OPB
Therefore, OP is the angle bisector of ∠APB and ∠AOB
Hence, ∠OPA = ∠OPB = 1/2 (∠APB )
= 1/2 × 80°
= 40°
By angle sum property of a triangle,
In ΔOAP
∠A + ∠POA + ∠OPA = 180°
OA ⊥ AP (Theorem 10.1 : The tangent at any point of a circle is perpendicular to the radius through the point of contact.)
Therefore, ∠A = 90°
90° + ∠POA + 40° = 180°
130° + ∠POA = 180°
∠POA = 180° - 130°
∠POA = 50°
Q12. Two concentric circles are of the radii 5 cm and 3 cm. Find out the length of a chord of the larger circle which touches the smaller circle.
 View Answer
View Answer 
Sol: The chord of the larger circle is a tangent to the smaller circle as shown in the figure below.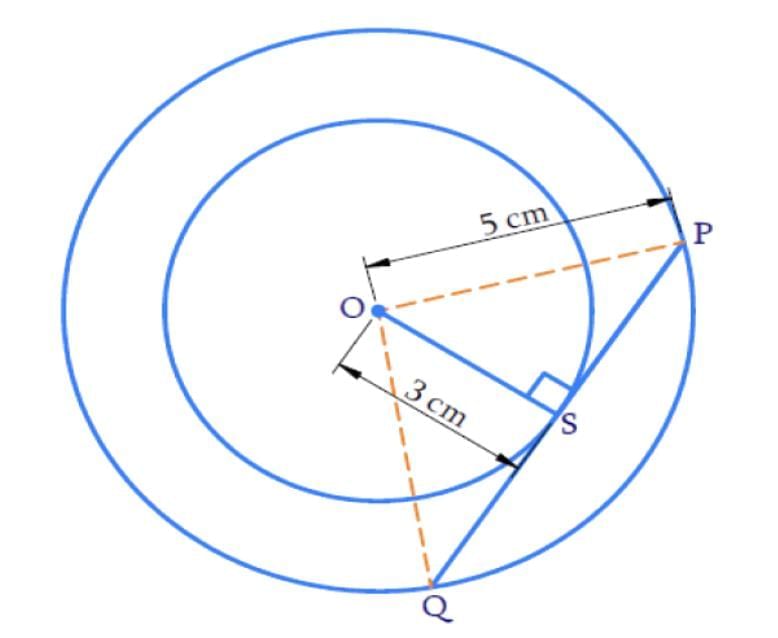
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle
PQ is a chord of a larger circle and a tangent of a smaller circle.
Tangent PQ is perpendicular to the radius at the point of contact S.
Therefore, ∠OSP = 90°
In ΔOSP (Right-angled triangle)
By the Pythagoras Theorem,
OP2 = OS2 + SP2
52 = 32 + SP2
SP2 = 25 - 9
SP2 = 16
SP = ± 4
SP is the length of the tangent and cannot be negative
Hence, SP = 4 cm.
QS = SP (Perpendicular from center bisects the chord considering QP to be the larger circle's chord)
Therefore, QS = SP = 4cm
Length of the chord PQ = QS + SP = 4 + 4
PQ = 8 cm
Therefore, the length of the chord of the larger circle is 8 cm.
Q13. From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the perimeter of the triangle PCD
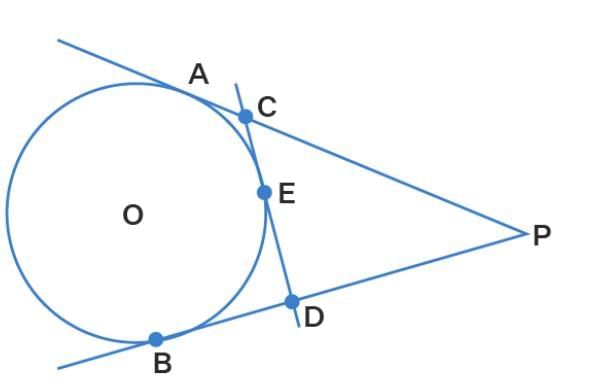
 View Answer
View Answer 
Sol: Given, PA and PB are the two tangents drawn to a circle with centre O though an external point P.
At point E on the circle the tangent is drawn which intersects PA and PB at C and D.
Given, PA = 10 cm
We have to find the perimeter of the triangle PCD.
We know that the tangents drawn to a circle through an external point are equal.
From the figure,
The tangents drawn through point P are PA and PB
So, PA = PB -------------- (1)
The tangents to the circle through C are CA and CE
So, CA = CE -------------- (2)
The tangents to the circle through D are DB = DE
So, DB = DE -------------- (3)
Considering triangle PCD,
Perimeter = PC + PD + CD
From the figure,
CD = CE + DE
So, perimeter = PC + PD + CE + DE
From (2) and (3),
Perimeter = PC + PD + CA + DB
On rearranging,
Perimeter = PC + CA + PD + DB
From the figure,
PC + CA = PA
PD + DB = PB
By (1), PA = PB
So, perimeter = PA + PB
Perimeter = PA + PA
= 2PA
Given, PA = 10 cm
So, 2PA = 2(10)
= 20 cm
Therefore, the perimeter of the triangle PCD is 20 cm.
Q14. In Fig. 9.10, PQL and PRM are tangents to the circle with centre O at the points Q and R, respectively and S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°. Then ∠QSR is equal to 40°. Write ‘True’ or ‘False’ and give reasons for your answer

 View Answer
View Answer 
Sol: False
Given, PQL and PRM are the tangents to the circle with centre O at the points Q and R
S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°
We have to determine if ∠QSR is equal to 40°.
We know that the radius of circle is perpendicular to the tangent at the point of contact.
So, ∠LQO = ∠MRO = 90°
From the figure,
∠LQO = ∠LQS + ∠SQO
90° = 50° + ∠SQO
∠SQO = 90° - 50°
∠SQO = 40°
From the figure,
∠MRO = ∠MRS + ∠SRO
90° = 60° + ∠SRO
∠SRO = 90° - 60°
∠SRO = 30°
Considering triangle OSQ,
OS = OQ = radius
Two sides of a triangle are equal
So, OSQ is an isosceles triangle.
In an isosceles triangle, two sides and two angles are equal.
Two equal angles are ∠SOQ = ∠ORS
∠QSR = ∠OSQ + ∠OSR
∠QSR = 30° + 40°
Therefore, ∠QSR = 70°
Q15. In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.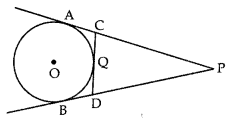
 View Answer
View Answer 
Sol: Given: PA and PB are the tangents to the circle.
PA = 12 cm
QC = QD = 3 cm
To find: PC + PD
PA = PB = 12 cm (The lengths of tangents drawn from an external point to a circle are equal)
Similarly, QC = AC = 3 cm and QD = BD = 3 cm.
Now, PC = PA - AC = 12 - 3 = 9 cm
Similarly, PD = PB - BD = 12 - 3 = 9 cm
Hence, PC + PD = 9 + 9 = 18 cm.
|
127 videos|685 docs|84 tests
|
FAQs on Practice Questions: Circles - Mathematics (Maths) Class 10
| 1. What are some popular hobbies that involve circles? |  |
| 2. How can I incorporate circles into my creative hobbies? |  |
| 3. What are the benefits of engaging in hobbies that involve circular movements? |  |
| 4. Are there any specific tools or equipment needed for circle-related hobbies? |  |
| 5. How can I find local groups or classes for circle-based hobbies? |  |





















