Class 10 Exam > Class 10 Notes > Mathematics (Maths) Class 10 > Practice Questions: Introduction to Trigonometry
Practice Questions: Introduction to Trigonometry | Mathematics (Maths) Class 10 PDF Download
Questions
1. If sin 3θ = cos (θ – 6)° and 30 and (θ – 6)° are acute angles, find the value of θ.
2. If 3 cot A = 4, find the value of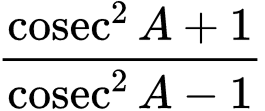 
.
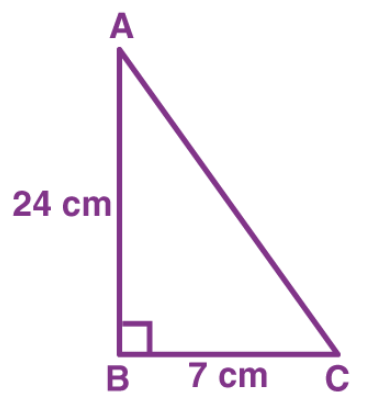
3. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm.
Determine:
(i) sin A, cos A
(ii) sin C, cos C
4. Evaluate 2tan2 45° + cos2 30° – sin2 60°.
5. If sin θ + cos θ = √2, then evaluate tan θ + cot θ.
6. If sin θ + sin2θ + sin3θ = 1, then find the value of cos6 θ – 4 cos4 θ + 8 cos2 θ.
7. What is the value of 0, for sin2θ = 1, where 0° < θ < 90°?
8. In ∆ABC, ∠B = 90°. If AB = 14 cm and AC = 50 cm then tan A equals?
9. If 4 cot θ = 3 then what is the value of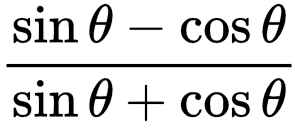 
?
10. What is the value of cosec2 27° – tan2 63°?
11. If ∆ABC is right angled at C, then what is the value of cos(A + B)?
12. If 3 cos θ = 1, then what is the value of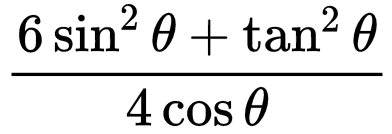 
?
13. Evaluate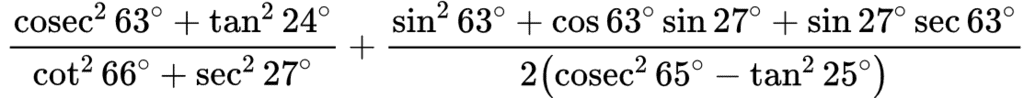 
14. If sin 3θ = cos (θ – 6)° and 30 and (θ – 6)° are acute angles, find the value of θ.
15. If sec 3A = cosec (A – 10°) where 3A is an acute angle, find the value of A.
Answers
1. θ = 24°
2. 17/8
3. (i) Sin A = 7/25 and cos A = 24/25
(ii) Sin C = 24/25 and Cos C = 7/25
4. 2
5. 2
6. 4
7. 45°
8. 7/24
9. 1/7
10. 1
11. 0
12. 10
13. 2
14. θ = 24°
15. A = 25°
The document Practice Questions: Introduction to Trigonometry | Mathematics (Maths) Class 10 is a part of the Class 10 Course Mathematics (Maths) Class 10.
All you need of Class 10 at this link: Class 10
|
127 videos|584 docs|79 tests
|
FAQs on Practice Questions: Introduction to Trigonometry - Mathematics (Maths) Class 10
| 1. What is the Pythagorean theorem and how is it applied in trigonometry? |  |
Ans. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In trigonometry, this theorem is fundamental because it relates the lengths of the sides of right triangles to the trigonometric functions sine, cosine, and tangent, which are defined based on these lengths.
| 2. How do you find the sine, cosine, and tangent of an angle in a right triangle? | |
Ans. To find the sine, cosine, and tangent of an angle (let's say angle A) in a right triangle, you use the following definitions:
- Sine (sin A) is the ratio of the length of the opposite side to the hypotenuse (sin A = opposite/hypotenuse).
- Cosine (cos A) is the ratio of the length of the adjacent side to the hypotenuse (cos A = adjacent/hypotenuse).
- Tangent (tan A) is the ratio of the length of the opposite side to the adjacent side (tan A = opposite/adjacent).
| 3. What are the key trigonometric identities that students should memorize? | |
Ans. Key trigonometric identities include:
- Pythagorean identities: sin²x + cos²x = 1.
- Angle sum identities: sin(A + B) = sin A cos B + cos A sin B; cos(A + B) = cos A cos B - sin A sin B.
- Double angle formulas: sin(2x) = 2sin x cos x; cos(2x) = cos²x - sin²x.
| 4. What is the unit circle and why is it important in trigonometry? | |
Ans. The unit circle is a circle with a radius of one centered at the origin of the coordinate plane. It is important in trigonometry because it provides a way to define the sine, cosine, and tangent functions for all angles, not just those in right triangles. Points on the unit circle correspond to the values of these functions, allowing for a visual representation of their behavior and periodicity.
| 5. How can trigonometry be applied in real-life scenarios? | |
Ans. Trigonometry has numerous real-life applications, including:
- In architecture and engineering, to calculate structural loads and angles.
- In navigation, for determining distances and angles between locations.
- In physics, to analyze wave patterns and oscillations.
- In computer graphics, for rendering 3D images and animations.
About this Document
1.5K Views
4.63/5
Rating
Sep 20, 2025
Last updated
Document Description: Practice Questions: Introduction to Trigonometry for Class 10 2025 is part of Mathematics (Maths) Class 10 preparation.
The notes and questions for Practice Questions: Introduction to Trigonometry have been prepared according to the Class 10 exam syllabus. Information about Practice Questions: Introduction to Trigonometry covers topics
like Questions, Answers and Practice Questions: Introduction to Trigonometry Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Practice Questions: Introduction to Trigonometry.
Introduction of Practice Questions: Introduction to Trigonometry in English is available as part of our Mathematics (Maths) Class 10
for Class 10 & Practice Questions: Introduction to Trigonometry in Hindi for Mathematics (Maths) Class 10 course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Practice Questions: Introduction to Trigonometry | Mathematics (Maths) Class 10
Description
Full syllabus notes, lecture & questions for Practice Questions: Introduction to Trigonometry | Mathematics (Maths) Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 10 | Best notes, free PDF download
Information about Practice Questions: Introduction to Trigonometry
In this doc you can find the meaning of Practice Questions: Introduction to Trigonometry defined & explained in the simplest way possible. Besides explaining types of
Practice Questions: Introduction to Trigonometry theory, EduRev gives you an ample number of questions to practice Practice Questions: Introduction to Trigonometry tests, examples and also practice Class 10
tests
Related Searches
Semester Notes
,Summary
,Sample Paper
,shortcuts and tricks
,MCQs
,Free
,ppt
,video lectures
,Practice Questions: Introduction to Trigonometry | Mathematics (Maths) Class 10
,practice quizzes
,past year papers
,mock tests for examination
,Previous Year Questions with Solutions
,Extra Questions
,Viva Questions
,Practice Questions: Introduction to Trigonometry | Mathematics (Maths) Class 10
,Objective type Questions
,Important questions
,Practice Questions: Introduction to Trigonometry | Mathematics (Maths) Class 10
,Exam
,study material
;
Additional Information about Practice Questions: Introduction to Trigonometry for Class 10 Preparation
Practice Questions: Introduction to Trigonometry Free PDF Download
The Practice Questions: Introduction to Trigonometry is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Practice Questions: Introduction to Trigonometry now and kickstart your journey towards success in the Class 10 exam.
Importance of Practice Questions: Introduction to Trigonometry
The importance of Practice Questions: Introduction to Trigonometry cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Practice Questions: Introduction to Trigonometry Notes
Practice Questions: Introduction to Trigonometry Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Practice Questions: Introduction to Trigonometry.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Practice Questions: Introduction to Trigonometry Notes on EduRev are your ultimate resource for success.
Practice Questions: Introduction to Trigonometry Class 10
The "Practice Questions: Introduction to Trigonometry Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Practice Questions: Introduction to Trigonometry on the App
Students of Class 10 can study Practice Questions: Introduction to Trigonometry alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Practice Questions: Introduction to Trigonometry,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Practice Questions: Introduction to Trigonometry is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup