Practice Questions: Number System | Quantitative Techniques for CLAT PDF Download
Q1: Find out the value of x for which 7396×51 is divisible by 11? 9?
Ans: Odd places digits sum= 1+x+9+7 =17+x
Even places digits sum = 5+6+3 =14
Difference between the two sums = 17+x – 14 = 3+x
As per divisibility rule (3+x) should be divisible by 11, therefore 11= x+3
x = 11 – 3 = 8
Q2: What should be subtracted from 2016 to make it completely divisible by 19?
Ans: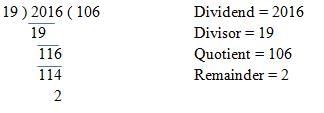
As we divide 2016 by 19 we get the remainder 2, that means when we subtract 2 from 2016 the number gets completely divisible.
Q3: Find the unit digit of the product (463 * 756 * 414 * 679).
Ans: For solving unit digit questions we don’t have to use whole numbers of products, only significant digits are of units place.
For such questions multiply all the digits at units place and what you get in the units place of the new number is the digit at units place of multiple of numbers given in question.
Multiple of digits at units place 3*6*4*9 = 18*36
Now here you might find yourself stuck with big numbers but it’s not that complicated. For such big numbers, you can again apply the same trick and it won’t change results i.e., 8*6 = 48
Thus the unit digit of (463 * 756 * 414 * 679) is 8
Q4: What is the total number of Prime factors in (47 * 75 *1111)
Ans: Given number: 47* 75 * 1111
Here we see other than 4, 7 and 11 are prime numbers but we also know that 4 is 2*2 which is a prime number. Thus we can rewrite the numbers as
(22 )7 * (7)5 * (11)11 = 214 *75 *1111
The no. of prime numbers would be the sum of numbers in power because that many prime numbers are there in the number ie., 14+5+11 = 30.
Q5: What is the nearest natural number to 8488, which is completely divisible by 77?
Ans: 8470
thus we see here 77*110 gives 8470 and 18 becomes remainder. Thus the nearest natural number is 8470.
Q6: Find out the smallest number to be subtracted from 13501, so that the remainder is divisible by 87.
Ans: 16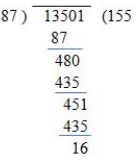
This is again a remainder question with just twisted language. If you find such questions in exam read th question twice-thrice and you would get the trick.
Q7: Find out the smallest 5 digit number which is divisible by 31?
Ans: The smallest 5 digit number is 10000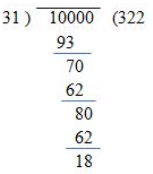
If 10000 is the smallest number and adding 31-18= 13 would make it divisible by 31.
Q8: Find out the largest 5 digit number which is divisible by 91?
Ans: The largest 5 digit number is 99999
If 99999 is the largest number and subtracting 81would make it divisible by 91.
Q9: If a number is divided by 56 then the remainder is 29. Find out the remainder if the same number is divided by 8.
Ans: Suppose a is the number being divided and b be the quotient
a = 56 *b + 29
= 8*7*b + 8*3 +5
= 8 ( 7*b + 3) +5
We need to divide a by 8 for fiding out the remainder, in the above explanation first part 8( 7*b + 3) have a factor 8 but 5 would still remain as remainder.
Q10: Find out how many numbers between 100 to 1000 are divisible by 6.
Ans: The first 3 digit number that is divisible by 6 is 102 and last would be 996 (you can find these numbers using smallest and largest methods we discussed earlier ).
This becomes an A.P. with a= 102, d=6 and l=996
l= a + (n-1)d
996 = 102 + (n-1) 6
After solving above equation we get n=150. Therefore 150 3 digit numbers which are divisible by 6.
|
49 videos|179 docs|73 tests
|
FAQs on Practice Questions: Number System - Quantitative Techniques for CLAT
| 1. What are the different types of number systems used in mathematics? |  |
| 2. How do you convert a decimal number to a binary number? |  |
| 3. How do you convert a binary number to a decimal number? |  |
| 4. What is the significance of the octal number system in computer programming? |  |
| 5. How was the Roman numeral system used in ancient times? |  |
















