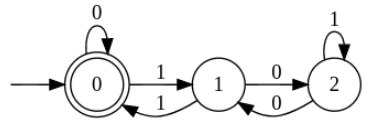
Q1: Let M be the 5-state NFA with ϵ-transitions shown in the diagram below:
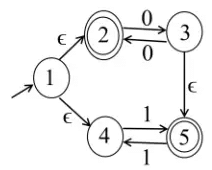
Which one of the following regular expressions represents the language accepted by M ? (2024 SET-2)
(a) (00)* + 1(11)*
(b) 0* + (1 + 0(00)*)(11)*
(c) (00)* + (1 + (00)*)(11)*
(d) 0 + + 1(11)* + 0(11)*
Ans: (b)
Sol:
Option A. here it is showing that even no of O's is accepted with odd no of 1's but if we try to find the solution for 00111 we cannot find with the help of given NFA
Option C. Here also if we will take an example for the string 00000 we won't be able to find in the given option but this string is accepted by the NFA
Option D. Here empty string is not present. Atleast 0 is always present. Hence this solution is also not correct.
Correct Answer is: B
Q2: Which one of the following regular expressions is equivalent to the language accepted by the DFA given below? (2024 SET-2)
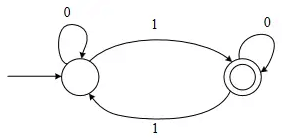
(a) 0*1(0 + 10*1)*
(b) 0*(10*11)*0*
(c) 0*1(010*1)*0*
(d) 0(1 + 0*10*1)*0*
Ans: (a)
Sol:
The given DFA accepts all & only binary strings containing Odd number of 1's.
So, option A is correct regular expression.
Option B Counter-Example: Generates empty string.
Option C Counter-Example: Doesn't generate 10011.
Option D Counter-Example: Doesn't generate 1.
WHY Option A: Go to the final state by reading 0*1, then stay in the final state by making either loop 0 or loop 10*1 in any order, any number of times. So, 0*1(0 + 10*1)* is the correct regular expression.
Q3: Consider the following two regular expressions over the alphabet {0, 1}:
r = 0* + 1*
S = 01* + 10*
The total number of strings of length less than or equal to 5, which are neither in r nor in s, is______ (2024 SET-1)
(a) 44
(b) 55
(c) 66
(d) 33
Ans:
Sol:
1. zero length string epselon can be formed using r.
2. all string with length 1 {a,b} can be formed using r.
3. in string with length 3, total 8 strings can be formed as there is three digit and for every digit we can select either 0 or 1, so 2 x 2 x 2 = 8.
Now As per RE r = {000, 111} and s = {011, 100) will be formed using RE r and s.
so strings of length 3 not present in both RE will be = 8 - 4 = 4.
4. For length 4, Similarly as 3rd steps
total string = 2 x 2 x 2 x 2 = 16
total strings not present in r and s = 16 - 4{0000, 1111, 0111, 1000} = 12.
5. For length 5, Similarly as 3rd steps
total string = 2 x 2 x 2 x 2 x 2 = 32
total strings not present in r and s = 32 - 4{00000, 11111, 01111, 10000} = 28.
So total string of length less than equal to 5 which are not present in both RE r and s will be 4 + 12 + 28 = 44(Option A).
Q4: Consider the following definition of a lexical token id for an identifier in a programming language, using extended regular expressions:
letter → A - Za - z
digit → [0 - 9]
id → letter(letter | digit)*
Which one of the following Non-deterministic Finite-state Automata with - transitions accepts the set of valid identifiers? (A double-circle denotes a final state) (2023)
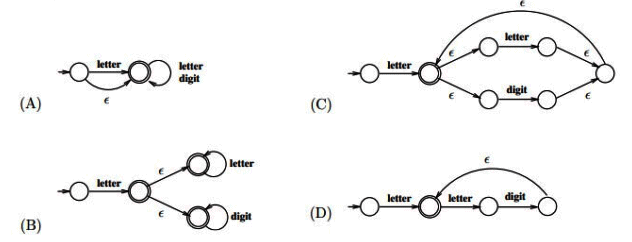
(a) A
(b) B
(c) C
(d) D
Ans: (c)
Sol:
The regular expression is given as letter (letter + digit)*.
This regular expression accepts the strings of one occurrence of a letter followed by any occurrence of letter and digits, such as (letter, letter.letter,letter.digit,letter.digit.digit..∞)
Option (A) This is wrong because it also accepts empty string that is ϵ.
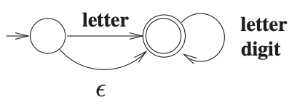
Option (B):
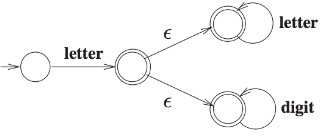
This is wrong because it accepts strings like (letter), (letter.letter) ...(letter.digit), (letter.digit.digit), but it will not accepts the strings like (letter.digit.letter).
Option (C): It is the correct option. it will accepts all the strings of letter (letter + digit)*
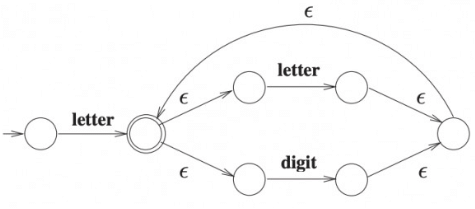
Option (D):
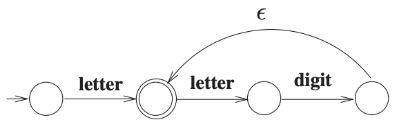
it is wrong. it RE is (letter(letter. digit)*)
and it will accept strings like (letter), (letter. letter. digit). (letter. letter. digit. letter. digit).....∞
it will not accepts strings like (letter. letter), (letter. digit) etc.
Q5: Consider the Deterministic Finite-state Automaton (DFA) A shown below. The DFA runs on the alphabet {0, 1}, and has the set of states (s, p, q, r), with s being the start state and p being the only final state.
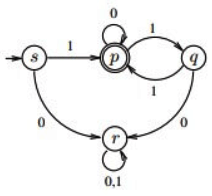
Which one of the following regular expressions correctly describes the language accepted by A? (2023)
(a) 1(0*11)*
(b) 0(0 + 1)*
(c) 1(0 + 11)*
(d) 1(110*)*
Ans: (c)
Sol:
The given finite automata generate string like
(1, 10, 111, 100, 11111, 1011, 1110, 10000, 101111, 10011...∞).
Start with 1 to reach the final state after that we have 2 choices as (0 + 11)*.
∴ R.E. = 1(0 +11)*
Option (A): it is wrong because it will not generate strings like 10
Option (B): it is wrong because it will generate 0 which is rejected in the given DFA.
Option (D): it is wrong because it will not generate strings like 10, 100.
Option (C) is correct.
Q6: Which of the following regular expressions represent(s) the set of all binary numbers that are divisible by three? Assume that the string ϵ is divisible by three. (2021 SET-2)
(a) (0 + 1(01*0)*1)*
(b) (0 + 11 + 10(1 + 00)*01)*
(c) (0*(1(01*0)*1)*)*
(d) (0 + 11 + 11(1 + 00)*00)*
Ans: (a, b and c)
Sol:
After this dfa is constructed, then by state elimination method we will directly get regular expression same as option A → (0 + 1(01*0)*1)* and now as per property (a + b)* = (a*b*)*, considering a as 0 and b as 1(01*0)1 we will get option c) (0* (1(01*0)1)*)* and now for option b and d we will check directly by checking the strings that will be accepted and from that we can observe that 1001(i.e.9) will not be accepted in option d)
Hence the ans A,B,C
Q7: Which one of the following regular expressions represents the set of all binary strings with an odd number of 1's? (2020)
(a) ((0 + 1)*1(0 + 1)*1)*10*
(b) (0*10*10*)*0*1
(c) 10* (0*10*10*)*
(d) (0*10*10*)*10*
Ans: (d)
Sol:
The regular expression should generate all possible binary strings with odd number of 1's and doesn't generate the other strings.
Option 1: Incorrect
Regular Expression: ((0 +1)*1(0 + 1)*1)*10*
String: 11110
It can generate strings (11110) with even number of 1's also
Option 2: Incorrect
Regular Expression: (0*10*10*)*0*1
It will generate string only ending with '1'
String: 1110
It cannot generate '1110' substring.
Option 3: Incorrect
Regular Expression: 10*(0*10*10*)*
It will generate string only starting with '1'
String: 0111
It cannot generate '0111' substring.
Option 4: Correct
Regular expression: 0*(10*10*)*10*
It will generate all possible binary strings with odd number of 1's and doesn't generate the other strings.
Q8: Which one of the following regular expressions represents the language: the set of all binary strings having two consecutive 0s and two consecutive 1s? (2016 SET-1)
(a) (0 + 1)*0011(0 + 1)* + (0 + 1)*1100(0 + 1)*
(b) (0 + 1)*(00(0 + 1)*11 + 11(0 + 1)*00)(0 + 1)*
(c) (0 + 1)*00(0 + 1)* + (0 + 1)*11(0 + 1)*
(d) 00(0 + 1)*11 + 11(0 + 1)*00
Ans: (b)
Sol:
Set of all binary strings having two consecutive Os and two consecutive 1s
Anything 00 Anything 11Anything + Anything 11 Anything 00 Anything
(0 + 1)*00(0 + 1)*11(0 + 1)* + (0 + 1)*11(0 + 1)*00(0 + 1)*
And it is same after taking common.
(0 + 1)*(00(0 + 1)*11 + 11(0 + 1)*00)(0 + 1)*
So, option B is answer.
Neither they said Both are immediate nor they give a predefined order, so it should be as above
Q9: The length of the shortest string NOT in the language (over ∑= {a, b}) of the following regular expression is________. (2014 SET-3)
a*b* (ba)* a*
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
Sol:
R = a*b*(ba)*a*
for finding shortest string that is not in language it is better to look strings of length 0, then of
length 1 and so on
length0{ϵ} is in L
length1{a, b} all belong to L
length2{aa, ab, ba, bb} all belong to L
length3{aaa, aab, aba, abb, baa, bab, bba, bbb} bab does not belong to L
Q10: Let L = {w ∈ (0+1)* / w has even number of 1s), i.e. L is the set of all bit strings with even number of 1s. Which one of the regular expressions below represents L? (2010)
(a) (0*10*1)*
(b) 0*(10*10*)*
(c) 0*(10*1)*0*
(d) 0*1(10*1)*10*
Ans: (b)
Sol:
A. -If the string contains a 1, it must end in a 1 hence cannot generate all bit strings with even number of 1's (eg, 1010)
B. - is the answer
C. - between the second and third 1's a 0 is not allowed (eg, 011011)
D. - 00 is not allowed, zero is an even number.






























