Previous Year Questions: Regular Language | Theory of Computation - Computer Science Engineering (CSE) PDF Download
Q1: Let L1 be the language represented by the regular expression b*ab* (ab8 ab8)8 and L2 = {w ∈ (a + b)*||w |≤ 4}, where |w| denotes the length of string w. The number of strings in L2 which are also in L1 is (2024 SET-2)
(a) 12
(b)15
(c) 18
(d) 20
Ans: (b)
Sol:
Let the language symbols = ∑ = {a, b} = |Σ| = 2.
If we try to analyze the regular language, we get L1 = set of strings where number of a's is odd.
For all strings with the alphabet set {a, b} of length 'n' half of them will have odd number of a's i.e. 2n/2 (numerator2 is based on the number of input symbols)
So, we can sum up half of total strings of all lengths (upto 4) in L1 =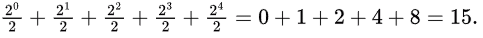
These all will be readily available in L2 since it is (a + b)*
Q2: Let L1, L2 be two regular languages and L3 a language which is not regular.
Which of the following statements is/are always TRUE? (2024 SET-1)
(a) L1 = L2 if and only if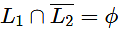
(b) L1 U L3 is not regular
(c) 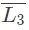 is not regular
is not regular
(d)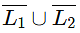 is regular
is regular
Ans: (c and d)
Sol:
A is wrong
As double implication we need to check both sides and take a case where L1 is subset of L2 still intersection of the statement will be null
Option B is wrong
because, take L1 as (a + b)*, now union of any non-regular language over alphabet a and b will always be regular.
Correct answers:
C and D
C is trivial and D is closure property where Regular languages are closed under both compliment and union.
Q3: Consider the following two statements about regular languages:
S1: Every infinite regular language contains an undecidable language as a subset.
S2: Every finite language is regular.
Which one of the following choices is correct? (2021 SET-2)
(a) Only S1 is true
(b) Only S2 is true
(c) Both S1 and S2 are true
(d) Neither S1 nor S2 is true
Ans: (c)
Sol:
S1: Every infinite regular language contains an undecidable language as a subset.
Cantor's theorem says that If S is any set then |S| < P(S), where P(S) is the power set of S.
So, from this we know that If we have any infinite set S then P(S) is definitely Uncountable (Because remember that a set A is countable if and only if |A| ≤ |N|, where N is the set of natural numbers).
From this we can say that if S is countably infinite set, then P(S) is uncountable.
We know that Every language is countable. (Every language L is a subset of ∑*, and ∑* is countable and subset of countable set is countable)
If we have any infinite language L, then it means that we have uncountably many subsets of
L. But we know that set of all RE languages is countable. So, due to this we have a subset of
L which is Not RE. So, the following statements are true :
- Every infinite regular language L has a subset S which is undecidable.
- Every infinite regular language L has a subset S which is unrecognizable.
- Every infinite language L has a subset S which is undecidable.
- Every infinite language L has a subset S which is unrecognizable.
- Here, (2) implies (1) and (4) implies (3) as undecidable set is a proper superset of unrecognizable set. (By undecidable set, I mean Set of all undecidable languages. Similarly, for unrecognizable set.
NOTE that if a language is unrecognizable then it is undecidable as well, so, undecidable set is a proper superset of unrecognizable set. Decidable set is a proper subset of Recognizable set because every decidable language is recognizable.)
Summary of above explanation:
EVERY language L is Countable. Every language, RE or Not RE, whatever language, is always Countable.
Set of all RE languages is Countable. Set of all Non-RE languages is Uncountable.
Now, If L is ANY infinite language, It has uncountable number of subsets. If every subset of L is a RE language, then we can have only countable number subsets of L, But I has uncountable number of subsets. That's why I has at least one subset which is Not-RE.
Actually, L has uncountable number of subsets which are Not-RE.
For regular languages, we can prove statement 1 using pumping lemma as well.
Using the pumping lemma, we find x, y, z such that xyn z is in language L for every n, and then consider the subset S = {xyn z | n ∈ A}, where A is any undecidable set of natural numbers. So, S is Not decidable.
S2 : Every finite language is regular.
It is true.
Proof:
Assume that we have a finite language L = {W1, W2, W3, ..., Wn}
For L we can write down:
Regular grammar:
- S → W1 | W2 | W3 |... | Wn
Regular expression:
- W1 + W2 + W3 + ... + Wn
Hence L is regular
Edit:
Some more variations :
The statement S1 can be written in Contrapositive manner as following:
S1 : Every infinite regular language contains an undecidable language as a subset.
Contrapositive of S1: If ALL the subsets of a regular language L are decidable then L is
finite.
Similarly, we can say, in contrapositive manner, that:
- If ALL the subsets of a regular language L are recognizable then L is finite.
- If ALL the subsets of a language L are decidable then L is finite.
- If ALL the subsets of a language L are recognizable then L is finite.
Q4: Let L {0, 1}* be an arbitrary regular language accepted by a minimal DFA with k states.
Which one of the following languages must necessarily be accepted by a minimal DFA with k states? (2021 SET-2)
(a) L - {01}
(b) L U {01}
(c) {0, 1}* - L
(d) L . L
Ans: (c)
Sol:
The question is asking about Number of states in minimal DFA.
If L is regular then so is L - {01}, so is L U {01}, so is L. L, so is {0, 1}* - L.
But if minimal DFA for L has k states then can we guarantee that minimal DFA for L - {01} will have k states ?? can we guarantee that minimal DFA for LU {01} will have k states ?? can we guarantee that minimal DFA for L. L will have k states ?? can we guarantee that minimal DFA for complement of L will have k states ??
First we will check Option C. We will prove that if minimal DFA for a regular language L has n states then the minimal DFA for complement of L will also have n states.
Since L is regular language, so, we have some DFA D that accepts L.
We can describe D as following: D(Q, Σ, δ, q0, F)
In this DFA D, If we make the accepting states be non-accepting, and make the non-accepting states be accepting, then this new automata D' can be described as D' (Q, Σ, δ, q0, Q - F) (Because in D', set of final states is QF) and this D' has following properties :
1. D' is a DFA (Because we are not changing the transition function so for every state, on every alphabet symbol we still have exactly one transitions)
2. Since D, D' have same states, same initial state, same transition function, So, on any string w, both D, D' will go to same state, say, q. Now, we have two cases:
- if q is final state in D then q is non-final in D', So, w ∈ L(D) and w & L(D')
- if q is non-final state in D then q is final in D', So, w & L(D) and w ∈ L(D')
So, any string w, either it belongs to L(D) or to L(D') But Not to both. So, L(D) and L(D') are complement of each other.
So, the conclusion is that :
If a DFA D accepts language L, then DFA D' will accept language L', where D' is constructed from D by changing the final states to Non-final and vice versa.
So far we have proven that If D is DFA for L then D' is DFA for L'.
Now, the second part is to prove that:
If D is minimal DFA for L then D' is minimal DFA for L'.
This is easy to prove by contradiction.
Let DFA D be the minimal DFA of L with n states in it.
For contradiction, let us assume that DFA D' is Not minimal DFA for L' then it means that L' has some minimal DFA M in which we have less than n states.
Now, we construct M' by swapping final and non-final states in M, So, M' will accept complement of L' i.e. M' accepts L. So, now we have a DFA (M') for L in which we have less than n states. But this is contradiction because minimal DFA for L has n states.
So, our assumption is false i.e. It is Not the case that DFA D' is Not minimal DFA for L'.
So, D' is minimal DFA for L'.
So, we have proven that:
If a D is a minimal DFA for a regular language L then D' is minimal DFA for L'.
Since D and D' have same number of states, so we can say that number of states in minimal DFA for regular language L and number of states in minimal DFA for complement of L is same.
Option A is false :
For counter example, take L = {01}, minimal DFA for L has 4 states. But minimal DFA for
L - {01} has 1 state only.
Option B is false :
For counter example, take L = {}, minimal DFA for L has 1 state. But minimal DFA for
L U {01} has 4 states.
Option D is false :
For counter example, take L = {0}, minimal DFA for L has 3 states. But minimal DFA for L. L has 4 states.
Q5: Consider the following statements.
I. If L1 ∪ L2 is regular, then both L1 and L2 must be regular.
II. The class of regular languages is closed under infinite union.
Which of the above statements is/are TRUE? (2020)
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Ans: (d)
Sol:
Keeping L2 as ∑*, what ever may be L1,, we get a Regular language.
So, statement I is wrong.
If regular languages are closed under infinite union, then L = {an . bn n > 0} must be
regular as it is equal to {ab} ∪ {aabb} ∪ {aaabbb} U...
So, statement Il is wrong.
Option D is correct.
Q6: For ∑ = {a, b}, let us consider the regular language
L = {x ∣ x = a2+3k or x = 610+12k, k ≥ 0}.
Which one of the following can be a pumping length (the constant guaranteed by the pumping lemma) for L? (2019)
(a) 3
(b) 5
(c) 9
(d) 24
Ans: (d)
Sol:
Pumping length P for a regular language L makes sure that any string in that language with the length greater than or equal to pumping length has some repetition zero or more times.
This means If you take w ∈ L such that length of w is greater or equal to P then some part of w can be pumped zero or more times such that resulting string is still in language.
For example, lets take regular language L = {0m1n∣m ≥ 0, n ≥ 0}. Here suppose somehow I know that pumping length is 1. Now you choose any string having length ≥ 1 then I will show you which substring you can pump (zero or more times). Note that you are free to remove subtsring (pumping zero times) or pump anytime.
- Suppose you choose 00011 (its length is 5 which is greater than equal to 1)
- I say ok, take first 0 and pump it zero or more times.
- You: Hmm, pumping first zero 0 times i.e. removing first 0 from 00011 or pumping one or more times will give string which is still in language.
Which means for any regular language you have pumping length. (Regular language satisfy pumping lemma)
But wait, Above pumping length is 1, can I say pumping length is also 2? (Yes, you can take any string which is greater or equal to 2 and pump some substring ot it).
Lets talk about minimum pumping length (MPL) only. Because of we know MPL then we know all pumping lengths. if MPL = P then P + k is also pumping length for any non-negative k.
We can also see pumping lemma using DFA and even regular grammar.
If we talk about DFA then it repeats some states. If we talk about regular grammar then it repeats atleast one nonterminal in derivation.
Let us suppose p is minimum pumping length then any string w that has length greater than equal to p must have repetition(zero or more times).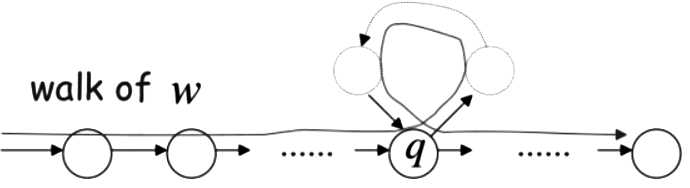
(In above DFA, for any string which has length > p it has to go through the loop (zero or more times).)
S → aX →...→ aw'X →...→ w
S →aX →...→aw'X →...→ aw'w'X → ...→ w (if repeat X 2 times)
If you notice we can generate infinitely many string by choosing number of repetitions to be 1,2,3 or any value.
Does this make any regular language an infinite language? No, we already know that regular languages are finite too.
What goes wrong here? Nothing.
For finite languages pumping length is greater than the longest string. And the definition of pumping length says that "Any string that is greater than equal to MPL p...". And there are no string which is greater than equal to MPL p which makes definition trivially true.
Now coming to the easiest part which is solving the question with clear definition in mind.
(First construct DFA)
Option A says that any string that has length 3 or greater has to have some repetition.
-Obviously false, b10 is a string in language and doesn't repeat any state.
Moreover any string with length greater than equal to 12 needs to repeat states.
D is the correct answer.
Q7: If L is a regular language over ∑ = {a, b}, which one of the following languages is NOT regular? (2019)
(a) L. LR = {xy|x ∈ L, YR ∈ L}
(b) {wwR|w ∈ L}
(c) Prifix(L) = {x ∈ Σ*|∃Υ ∈ Σ* such that xy ∈ L}
(d) Suffix(L) = {y ∈ Σ*|∃x ∈ Σ* such that xy ∈ L}
Ans: (b)
Sol:
wwR is well known CFL - the PDA can non-deterministically determine the middle position of the string and start popping (this is not DCFL though).
Reverse, Suffix, Prefix, Concatenation of Regular(s) is Regular.
Answer is (B).
Q8: Language L1 is defined by the grammar: S1 → as1b|ε
Language L2 is defined by the grammar: S2 → abS2|ε
Consider the following statements:
P: L1 is regular
Q: L2 is regular
Which one of the following is TRUE? (2016 SET-2)
(a) Both P and Q are true
(b) P is true and Q is false
(c) P is false and Q is true
(d) Both P and Q are false
Ans: (c)
Sol:
S1 → aS1b | ϵ
L1 = {anbn | n ≥ 0} is CFL
S2 → abS2 | ϵ
L2 = {(ab)n | n ≥ 0} is Regular having regular expression (ab)*
Q9: Which of the following languages is/are regular? (2015 SET-2)
L1 : {wxwR|w, x ∈ {a, b}* and |w|, |x| > 0}, wR is the
reverse of string w
L2 : {anbm|m ≠ n and m, n ≥ 0}
L3 : {apbqcr|p, q, r ≥ 0}
(a) L1 and L3 only
(b) L2 only
(c) L2 and L3 only
(d) L3 only
Ans: (a)
Sol:
L1: all strings of length 3 or more with same start and end letter- because everything in middle can be consumed by x as per the definition of L.
L2: We need to compare number of a's and b's and these are not bounded. So, we need at least a DPDA.
L3: Any number of a's followed by any number of b's followed by any number of c's. Hence regular.
Q10: Let L1 = {w ∈ {0, 1} * | w has at least as many occurrences of (110)'s as (011)'s).
Let L2 = {w ∈ {0,1} * | w has at least as many occurrence of (000)'s as (111)'s).
Which one of the following is TRUE? (2014 SET-2)
(a) L1 is regular but not L2
(b) L2 is regular but not L1
(c) Both L1 and L2 are regular
(d) Neither L1 nor L2 are regular
Ans: (a)
Sol:
Though at first look both L1 and L2 looks non-regular, L1 is in fact regular. The reason is the relation between 110 and 011.
We cannot have two 110's in a string without a 011 or vice verse. And this would mean that we only need a finite number of states to check for acceptance of any word in this language.
That was just an intuitive explanation. Now I say that L contains all binary strings starting with 11. Yes, if a binary string starts with 11, it can never have more no. of 011 than 110.
Lets take an example:
11 011 011-There are two 011's. But there are also two 110's. Similarly for any binary string starting with 11.
Using this property, DFA for L1 can be constructed as follows: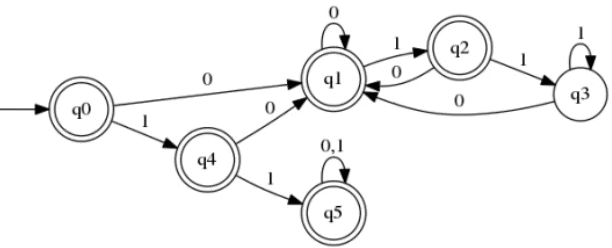
Q11: If L1 = {a" n ≥ 0} and L2 = {bn n ≥ 0}, Consider
(I) L1 . L2 is a regular language
(II) L1 . L2 = {anbn n ≥ 0}
Which one of the following is CORRECT? (2014 SET-2)
(a) Only (I)
(b) Only (II)
(c) Both (I) and (II)
(d) Neither (I) nor (II)
Ans: (a)
Sol:
L1 = {ε, a, aa, aaa, aaaa, ...}
L2 = {ε, b, bb, bbb, bbbb, ...}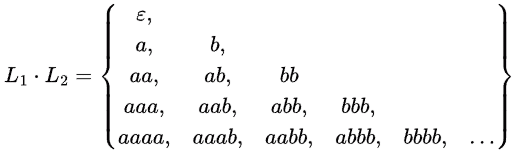
L1 . L2 = a*b*
Thus, L1 . L2 is Regular.
(Also, since both L1 and L2 are Regular, their concatenation has to be Regular since Regular languages are closed under concatenation)
However, L1 L2 ≠ anbn. This is because in a*b*, the number of a's and b's can be different where as in anbn they have to be the same.
Q12: Which one of the following is TRUE? (2014 SET-1)
(a) The language L = {anbn > 0} is regular
(b) The language L = {an | n is prime} is regular
(c) The language L = { w | w has 3k +1 b's for some k ∈ N with ∑ = {a, b} } is regular.
(d) The language L = { ww | w∈ ∑* with = 0,1}} is regular.
Ans: (c)
Sol:
L= anbn n ≥ 0 is a CFL because we are pushing suppose (n = 2) 2 no. of a and for every b we are pop out one 'a' so we are end with empty stack so string is accepted.so this is accepted by PDA as stack is required there.
L = an / n is prime no. is CSL not CFL because we are pushing only the no. of 'a' and no other no. to pop i out and n is prime no. making is CSL.
L = {w/w has 3k + 1 b's for some k ∈ N with ∑ = {a, b} is a regular since total number of b's are multiple of 3 plus 1, as we can draw DFA for this.
L = ww/w ∈ Σ* with ∑ = {0, 1} is csl because 010101010101 as we do not know where to push and where to pop out so it is not CFL and L = ww is not regular because we can not have regular expression for this.
so the option c is correct.
Q13: Consider the languages L1 = ϕ abd L2 = {a}. Which one of the following represents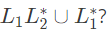 (2013)
(2013)
(a) {ϵ}
(b) ϕ
(c) a*
(d) {ϵ, a}
Ans: (a)
Sol:
Concatenation of empty language with any language will give the empty language and
L1* = c = ϵ.
Therefore,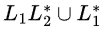
= ϕ. (L2)* U ϕ*
= ϕ U {ϵ} (∵ ϕ concatenated with anything is ϕ and ϕ* = {ϵ})
= {ϵ}.
Hence, option (A) is true.
PS: ϕ* = ϵ, where ϵ is the regular expression and the language it generates is {ϵ}.
Q14: Given the language L = {ab, aa, baa), which of the following strings are in L*? (2012)
1) abaabaaabaa
2) aaaabaaaa
3) baaaaabaaaab
4) baaaaabaa
(a) 1, 2 and 3
(b) 2, 3 and 4
(c) 1, 3 and 4
(d) 1, 2 and 4
Ans: (d)
Sol:
L = {ab, aa, baa}
Correct Answer: D
|
18 videos|93 docs|44 tests
|
FAQs on Previous Year Questions: Regular Language - Theory of Computation - Computer Science Engineering (CSE)
| 1. What is a regular language in computer science? |  |
| 2. How are regular languages different from context-free languages? |  |
| 3. Can regular languages be represented by regular expressions? |  |
| 4. What are some common examples of regular languages? |  |
| 5. How are regular languages used in practical applications of computer science? |  |
















