Previous Year Questions: Finite Automata | Theory of Computation - Computer Science Engineering (CSE) PDF Download
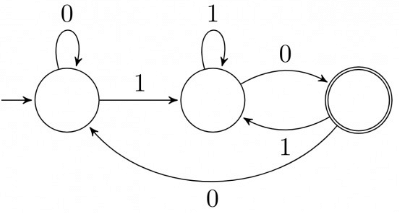
Q1: Consider the 5-state DFA M accepting the language L(M) ⊂ (0 + 1)* shown below. For any string w ∈ (0 + 1)* let n0 (w) be the number of 0's in w and n1 (w) be the number of 1 's in w.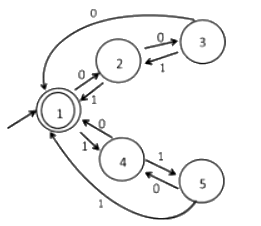
Which of the following statements is/are FALSE? (2024 SET-1)
(a) States 2 and 4 are distinguishable in M
(b) States 3 and 4 are distinguishable in M
(c) States 2 and 5 are distinguishable in M
(d) Any string w with n0 (w) = n1 (w) is in L(M)
Ans: (b, c)
Sol:
When we try to minimize the DFA given we can notice that states 3 and 4 have same inward and outward transitions and are indistinguishable, same for the states 2, 5.
States 2 and 4 are distinguishable, because they have different transitions from state 1.
In the final minimised DFA, we can clearly see that there are three states 1, 2, 4. For any given string with equal number of 1s and Os, it will be accepted by the DFA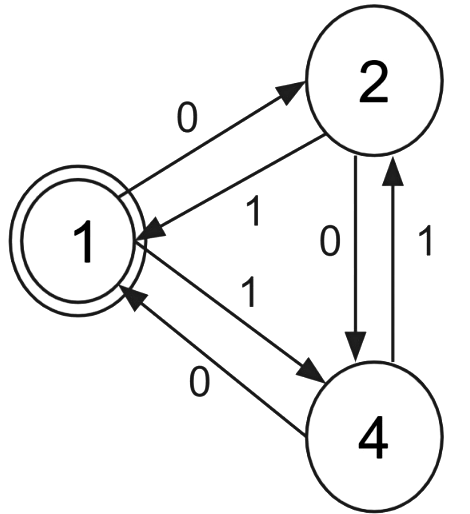
Q2: Consider the language L over the alphabet {0, 1}, given below:
L = {w ∈ {0, 1}* ∣w does not contain three or more consecutive 1's}.
The minimum number of states in a Deterministic Finite-State Automaton (DFA) for L is (2023)
(a) 3
(b) 4
(c) 5
(d) 6
Ans: (b)
Sol:
the given problem is simply a complement of MDFA having 3 consecutive 1's over the input (0, 1). We can take complement by simply changing the non-final state to the final state and vice-versa.
The MDFA not containing 3 or more consecutive 1's will require 4 state out of which 3 are final and 1 is dead states.
it will accept strings like (ϵ, 0, 1, 00, 01, 10, 11, 000, 001, 010, 011, 100, 101, 110...∞)
it will reject strings like (111, 1110, 11101, 11111, 111000, 1110101, 111001...∞)
the correct MDFA is as follows: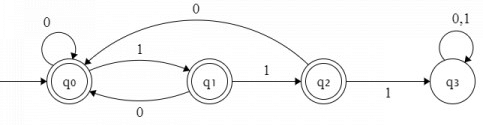
Q3: Which one of the following regular expressions correctly represents the language of the finite automaton given below? (2022)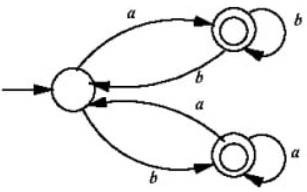
(a) ab*bab* + ba*aba*
(b) (ab*b)*ab* + (ba*a)*ba*
(c) (ab*b + ba*a)*(a* + b*)
(d) (ba*a + ab*b)*(ab* + ba*)
Ans: (d)
Sol: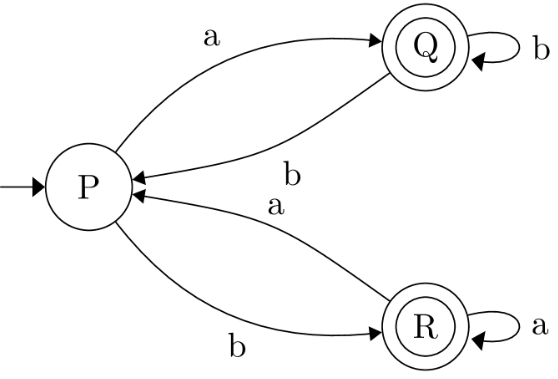
We have two final states, Q, R.
First find the regular expression for set of all strings that end up at the initial state P when running the given NFA. Let's call this P.
Note that P is the initial state, so, NFA execution starts at P. Now, to end up on state P at the end of the string, we can do any of the following, in any order, any number of times :
- Read 'a', go to state Q, then read any number of b's, then read b to come back to state P. So, 1 = ab*b
- Read 'b', go to state R, then read any number of a's, then read a to come back to state P. So, 2 = ba*a
So, P = (1 + 2)* = [(ab*b) + (ba*a)]* (Because we can do 1 or 2 in any order, any number of times)
Now, we want to find language of the given NFA N, whose final states are Q, R.
So, RegEx(N) = Q + R
Where Q is the regular expression for set of all strings that end up at the state Q when running the given NFA and R is the regular expression for set of all strings that end up at the state R when running the given NFA.
Q = Pab*
R = Pba*
So, RegEx(N) = Q + R Pab* + Pba* = P(ab* + ba*)
RegEx(N) = [(ab*b) + (ba*a)]*(ab* + ba*)
Hence, Option D is Correct Answer.
Method 2 (Option Elimination):
Option A:
The Strings "a" and "b" are accepted by the given NFA BUT these strings are Not generated by the regular expression in Option A. So Option A is wrong.
Option B:
The String abbbbaa is accepted by the given NFA BUT this string is Not generated by the regular expression in Option B. So Option B is wrong.
Option C:
The Empty String is NOT accepted by the given NFA BUT this string is generated by the regular expression in Option C. So Option C is wrong.
Correct answer is D.
Q4: Suppose we want to design a synchronous circuit that processes a string of O's and 1's. Given a string, it produces another string by replacing the first 1 in any subsequence of consecutive 1's by a 0. Consider the following example.
Input sequence: 00100011000011100
Output sequence: 00000001000001100
A Mealy Machine is a state machine where both the next state and the output are functions of the present state and the current input. The above mentioned circuit can be designed as a two-state Mealy machine. The states in the Mealy machine can be represented using Boolean values 0 and 1. We denote the current state, the next state, the next incoming bit, and the output bit of the Mealy machine by the variables s, t, b and y respectively. Assume the initial state of the Mealy machine is 0.
What are the Boolean expressions corresponding to t and y in terms of s and b? (2021 SET-2)
(a)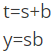
(b)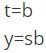
(c)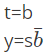
(d)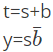
Ans: (b)
Sol: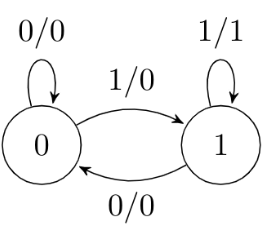
In (a / b), 'a' is input and 'b' is output
Option B is correct.
Q5: Consider the following deterministic finite automaton (DFA)
The number of strings of length 8 accepted by the above automaton is _________ (2021 SET-2)
(a) 32
(b) 256
(c) 64
(d) 512
Ans: (b)
Sol:
We can reach the final state with all possible strings of length three on set {0, 1}.
So there are 8 ways to reach the final state and we will have a five-length string remaining where we have two options - either 0 or 1, for each of the 5 positions.
So, total number of strings accepted will be 8 x 25 = 28 = 256.
The answer is 256.
Q6: Consider the following language:
L = { w ∈ {0, 1}* ∣ w ends with the substring 011}
Which one of the following deterministic finite automata accepts L? (2021 SET-1)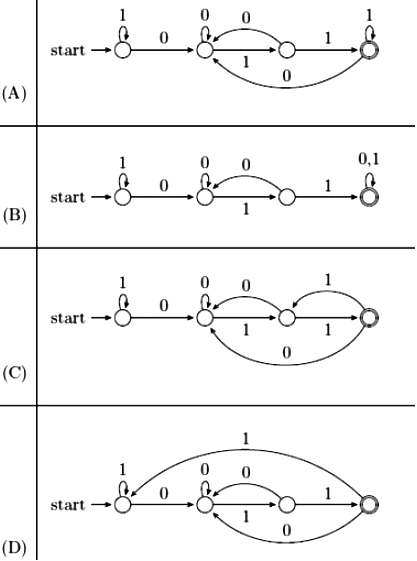
(a) A
(b) B
(c) C
(d) D
Ans: (d)
Sol:
The correct automata for L must accept every binary string ending with "011" and not accept any other binary string.
A. False it accepts binary strings ending with 111
B. False it accepts binary strings ending with 0, 00, 00, 100, 001, 111 etc.
C. False it accepts binary string ending with 1111
D. True it accepts all strings that end with 011 and no other strings.
Correct Ans: D
Q7: Consider the following language.
L = {x ∈ {a, b}* number of a's in x divisible by 2 but not divisible by 3}
The minimum number of states in DFA that accepts L is (2020)
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (c)
Sol:
Number of a's in x are divisible by 2 but not divisible by 3 means number of a's can be 2, 4, 8, 10, 14, 16, 20, 22, 26,...
Terms which are divisible by both 2 and 3 like 6, 12, 18, 24, ... are dropped from the above sequence at finite interval in * position from above sequence 2, 4, *, 8, 10, *, 14, 16, *, 20, 22, *, 26, 28, *, 32, 34, ...
Here, sequence {6, 12, 18, 24, ...} is in AP. Now, to drop this sequence from our original sequence which represent the number of a's, we have to go through at least total 7 states which says total 6 a's have seen so far and since terms of this sequence come at regular interval, So, we will make a cycle in the DFA as :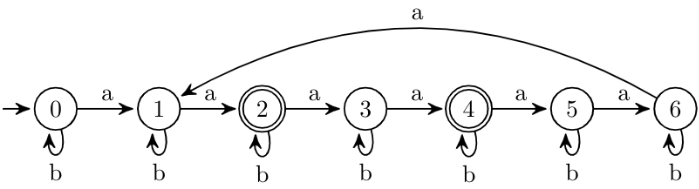
Now, observe that states 0 and 6 are equivalent because by definition, 2 states p and q are equivalent i.e.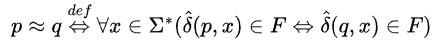
It says 2 states are equivalent if for all strings, they both either go to final state or both go to non-final state means they have the same nature.
So, here, we can merge states 0 and 6. Other states can't be merged because they are in cycle and if we merge states which are in cycle, machine will not accept the desired number of a's and reject 6, 12, 18, ... a's.
So, our final collapsing DFA is: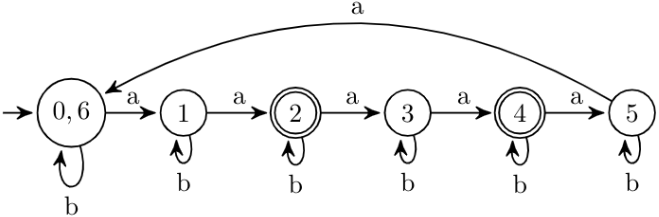
Q8: Let ∑ be the set of all bijections from {1,...,5} to {1,...,5}, where id denotes the identity function, i.e. id(j) = j, ∀j. Let o denote composition on functions. For a string x =x1x2...xn ∈ ∑n, n ≥ 0, let π(x) = x1 o x2 o ... o xn. Consider the language L = {x ∈ ∑* | π(x) = id}. The minimum number of states in any DFA accepting L is_______. (2019)
(a) 25
(b) 125
(c) 120
(d) 150
Ans: (c)
Sol:
I am rewriting question in (hopefully) simple way-
There are 5! 120 bijection functions possible. let f1, f2, ... f120 be functions. we can represent every function fi with some string xi.
Now we take the composition of functions f i and fj then the corresponding string is xixj (Composition of two functions in function space is the concatenation of corresponding strings in string space).
eg: Composite function fi o fj o fk has representation xixjxk and so on.
A function can have multiple string representations, suppose f i = fj o fk then fi has xi and xjxk both representations. And further, suppose f i = fp o fq o fr then fi = fp o fq o fr, then xpxqxr, also maps to = f i.
There is a given function called π which does the same job. i.e. π maps a string to the corresponding function. (It is obvious to see that π is many to one function.)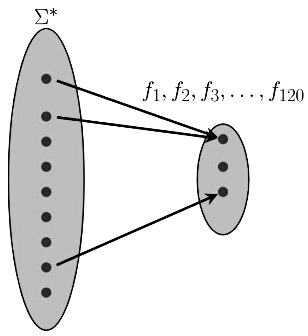
We need to construct a DFA, which accepts a set of all strings whose function representation behaves like Identity function.
x1x2... xn is accepted If and Only If f1 o f2 o ... o fn is identity function.
In other words, Design a DFA for L = π-1 (id).
First interesting and important point to note is, π(ϵ) = id.
Quick check for above statement: Suppose it is not the case and π(ϵ) is some nonidentity function f. Then consider a string x1x2x3 which maps to a function f123 (where f123 = f1 o f2 o f3) i.e. π(x1x2x3) = f1 o f2 o f3 o = f123. Now we can always append epsilon to a string x1x2x3 = x1x2x3ϵ
π(x1x2x3ϵ) = f1 o f2 o f3 o f = f123 o f ≠ f123.
This concludes that π(ϵ) = id, therefore, ∑ = {x1, x2, ... , x120} which has 120 states corresponding to 120 functions.
Initial state and final state will be the same which corresponds to the Identity function.
For any string xixj, DFA will move to state corresponding to function fi o fj and let fk = f i o fj. Therefore on string xixj, DFA will be in state corresponding to function fk.
(I have written fk = f i o fj, where fk is one of the function in f1, f2, ... , f120, because this set of bijective functions {f1, f2,, f120} is closed under composition).
Formally, we have DFA M = (∑, Q, q0, δ, F) for L = π-1(id).
where, ∑ = {x1, x2,..., x120}
Q = {f1, f2,..., f120} (let name of ith state is f i)
q0 = fid (f id is identity function)
δ(f i, a) = f1 o π(a), ∀a ∈ ∑
F = {f id}.
Q9: Given a language L, define L' as follows: (2018)
L0 = {ϵ}
Li = Li-1. L for all i > 0
The order of a language L is defined as the smallest k such that Lk = Lk+1, Consider the language L1 (over alphabet 0) accepted by the following automaton.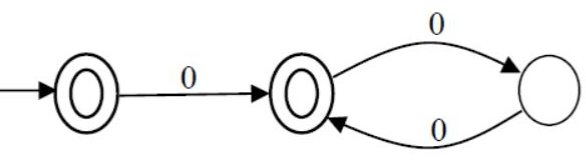
The order of L1 is ______
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol:
L1 = {ϵ + 0(00)*}
Now that is given language L, we have find order of it.
L0 = {ϵ}
L1 = L0. L = {ϵ}. {ϵ + 0(00)*} = {ϵ + 0(00)*}
L2 = L1 L = {ϵ + 0(00)*}. {ϵ + 0(00)*}
= {ϵ + 0(00)* + 0(00)*0(00)*}
L2 = {0*}
L3 = L2. L = {0*}. {ϵ + 0(00)*}
= {0* + 0*0(00)*}
L3 = {0*}
Order of L is 2 such that L2 = L2+1
Q10: Let N be an NFA with n states. Let k be the number of states of a minimal DFA which is equivalent to N. Which one of the following is necessarily true? (2018)
(a) k ≥ 2n
(b) k ≥ n
(c) k ≤ n2
(d) k ≤ 2n
Ans: (d)
Sol:
Number of states in minimal DFA - K must be ≤ 2n as each state corresponds to a subset of states of the corresponding NFA
D is answer.
Option B is not always TRUE as the NFA N can have epsilon moves and hence can have more number of states than the minimal DFA.
Q11: Let δ denote that transition function and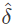 denote the extended transition function of the ϵ - NFA whose transition table is given below: (2017 SET-2)
denote the extended transition function of the ϵ - NFA whose transition table is given below: (2017 SET-2)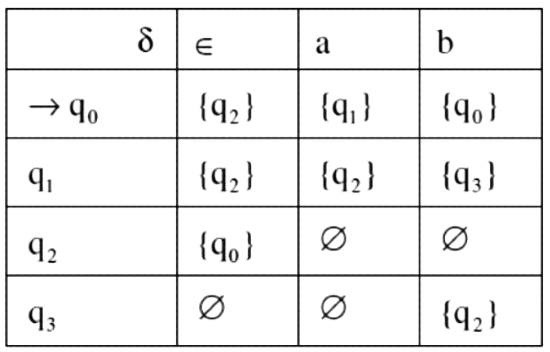
Then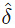 (q2, aba) is
(q2, aba) is
(a) ∅
(b) {q0, q1, q3}
(c) {q0, q1, q2}
(d) {q0, q2, q3
Ans: (c)
Sol:
Starting state: q2 and input string is "aba"
- Step 1: Find Epsilon closure of q2 = {q2, q0}
- Step 2: Find transitions on a:
- q0 → q1
- q2 → ∅
- Step 3: Find epsilon closure of q1 = {q1, q2, q0}
- Step 4: Find transitions on b:
- q1 → q3
- q0 → q0
- q2 → ∅
- Step 5: Find epsilon closure of q0 = {q0, q2} UNION epsilon closure of q3 = {q3}, = {q0, q2, q3}
- Step 6: Find transitions on a:
- q0 → q1
- q2 → ∅
- q3 → ∅
- Step 7: Find epsilon closure of q1 : {q1, q0, q2}
Therefore answer is C.
Q12: The minimum possible number of states of a deterministic automaton that accepts the regular language
L = {w1aw2∣w1, w2 ∈ {a, b}* , ∣ w1∣ = 2, ∣ w2∣ ≥ 3} is ______ (2017 SET-2)
(a) 4
(b) 6
(c) 8
(d) 9
Ans: (c)
Sol:
Answer is 8 states included one trap state (8) and final state (7).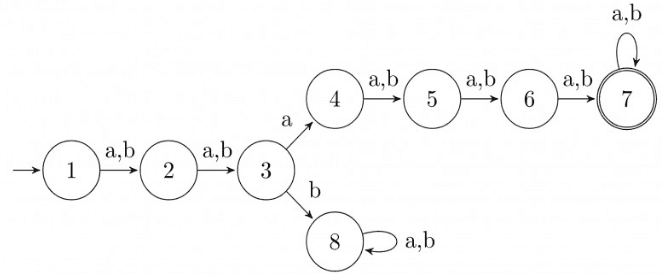
3rd symbol from the start is an a
Q13: Consider the language L given by the regular expression (a + b)* b (a + b) over the alphabet {a, b}. The smallest number of states needed in a deterministic finite-state automation (DFA) accepting L is ______ (2017 SET-1)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (c)
Sol: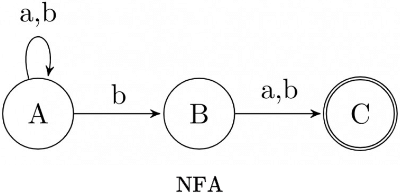 N
N
FA to DFA Conversion:
In the State Transition Table below we can see 4 states (A, AB, *AC, *ABC, the * ones being FINAL) are there but before confirming the ans lets try to minimize. A, AB cannot be minimized further because A goes to non-final state on a where as AB goes to a final state. Similarly *AC goes to a non-final state on a where as *ABC goes to a final state. Hence, none of the states can be merged.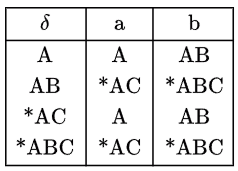
Answer: 4.
Q14: Consider the following two statements:
I. If all states of an NFA are accepting states then the language accepted by the NFA is ∑*
II. There exists a regular language A such that for all languages B, ANB is regular.
Which one of the following is CORRECT? (2016 SET-2)
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Both I and II are false
Ans: (b)
Sol:
I. False, as in NFA, it is not necessary that all states have transitions for all symbols.
II. True, there exists a regular language A = {}, such that for all languages B,
A ∩ B = {} is regular
So, Answer is option B.
Q15: The number of states in the minimum sized DFA that accepts the language defined by the regular expression
(0 + 1)* (0 + 1) (0 + 1)*
is _______. (2016 SET-2)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (a)
Sol:
All strings over {0, 1} having length ≥ 1
(0 +1)*(0 +1)(0 +1)* = (0 + 1)(0 + 1)* = (0 + 1)* (0 + 1) = (0 + 1)+
Having DFA: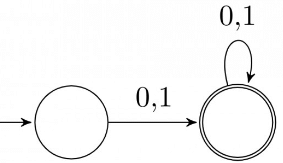
Number of states in minimal DFA = 2.
Q16: Let L be the language represented by the regular expression ∑* 0011∑* where ∑ = {0, 1}.
What is the minimum number of states in a DFA that recognizes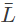 (complement of L)? (2015 SET-3)
(complement of L)? (2015 SET-3)
(a) 4
(b) 5
(c) 6
(d) 8
Ans: (b)
Sol:
First we can draw DFA for L which has 5 states after that for L compliment we will convert all final to non final and all non final to final so, total states is 5.
Answer is option B.
Q17: The number of states in the minimal deterministic finite automaton corresponding to the regular expression (0 + 1)*(10) is _____. (2015 SET-2)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
Sol:
All strings ending with 10. So, we need 3 states.
- From first state on 1, we go to second state.
- From second state on 0 we go to third state.
- From third state on 0 we go to first state and on 1 we go to second state.
Only third state is final.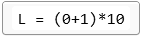 Minimal DFA will be as follows:
Minimal DFA will be as follows:
Q18: 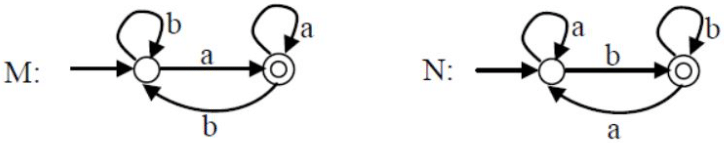
Consider the DFAs M and N given above. The number of states in a minimal DFA that accepts the language L(M) ∩ L(N) is ______ (2015 SET-1)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (a)
Sol:
L(M) = (a + b)* a = {a, aa, ba, aaa, aba, bba, ...}
L(N) = (a + b)* b = {b, ab, bb, aab, abb, bbb, ...}
So, L(M) ∩ L(N) = {}. So, in the minimal DFA, we just have 1 start state with all transitions going to it self and no final state.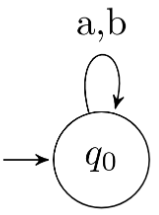
Q19: Which of the regular expressions given below represent the following DFA? (2014 SET-1)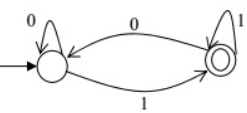
I) 0*1(1 + 00*1)*
II) 0*1*1 + 11*0*1
III) (0 + 1)*1
(a) I and II only
(b) I and III only
(c) II and III only
(d) I, II, and III
Ans: (b)
Sol:
The DFA accepts the language "all strings ending with 1".
So the regular expression corresponding to DFA is (0 + 1)*1.
Now, by using state elimination method,
So the DFA also has another equivalent regular expression: 0*1(1 + 00*1)*.
But the regular expression (0*1*1 + 11*0*1) is not equivalent to DFA, as the DFA also accept
the string "11011" which cannot be generated by this regular expression.
Q20: Consider the finite automaton in the following figure.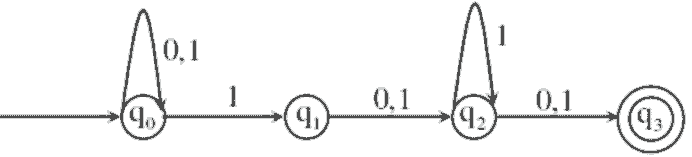
What is the set of reachable states for the input string 0011? (2014 SET-1)
(a) {q0, q1, q2}
(b) {q0,q1}
(c) {q0, q1, q2, q3}
(d) {q3}
Ans: (a)
Sol: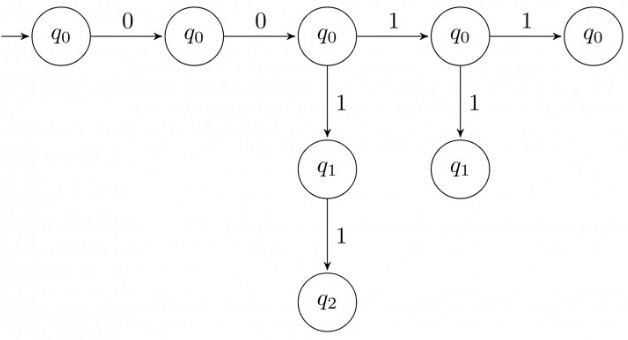
q0, q1 and q2 are reachable from q0 on input 0011
Correct Answer: A
Q21: Consider the DFA A given below.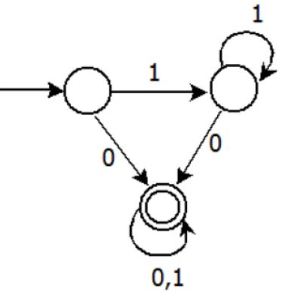
Which of the following are FALSE? (2013)
1. Complement of L(A) is context-free.
2. L(A) = L((11*0 + 0) (0 + 1)*0*1*)
3. For the language accepted by A, A is the minimal DFA.
4. A accepts all strings over {0, 1} of length at least 2.
(a) 1 and 3 only
(b) 2 and 4 only
(c) 2 and 3 only
(d) 3 and 4 only
Ans: (d)
Sol:
- Complement of L(A) (regular language) is regular and hence also Context Free. True
- Regular expression is (11*0 + 0)(0 + 1)* True
- Minimized DFA is:
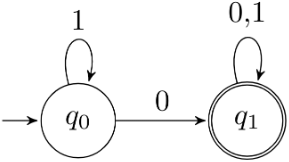
Both non-final states are equivalents and can be minimized
So, 3 is False - From 3, shortest length string reached from q0 to q1 (final) is 0, so 4 is False
Note :
a. (0 + 1)*0*1* = (0 + 1)* + something = (0 + 1)*
b. (11*0 + 0)(0 + 1)* = (11* + ϵ )0(0 + 1)* = 1*0(0 + 1)* look at Minimized DFA at 3.
Correct Answer: D
Q22: Consider the set of strings on {0, 1} in which, every substring of 3 symbols has at most two zeros. For example, 001110 and 011001 are in the language, but 100010 is not. All strings of length less than 3 are also in the language. A partially completed DFA that accepts this language is shown below. (2012)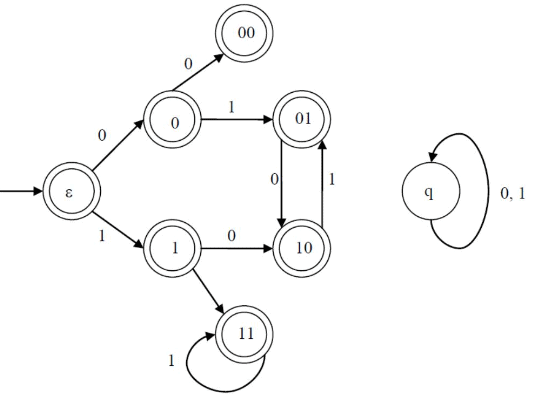
The missing arcs in the DFA are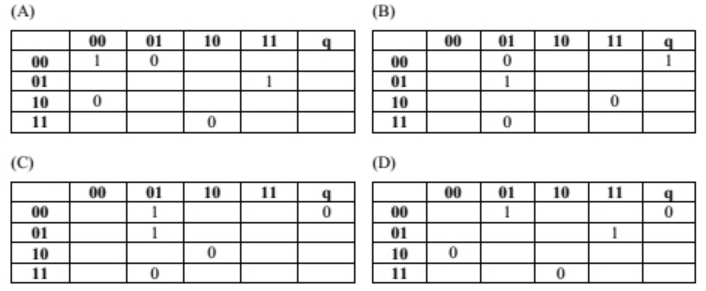
(a) A
(b) B
(c) C
(d) D
Ans: (d)
Sol:
(D) is the answer. From 00 state, a '0' should take the DFA to the dead state - q. From 11, a '0' should go to 10 representing the 10 at the end of string so far. Similarly, from 00 a 1 should go to 01, from 01 a '1' should go to 11 and from 10 a '0' should go to '00'.
Q23: What is the complement of the language accepted by the NFA shown below? Assume ∑ = {a} and ε is the empty string. (2012)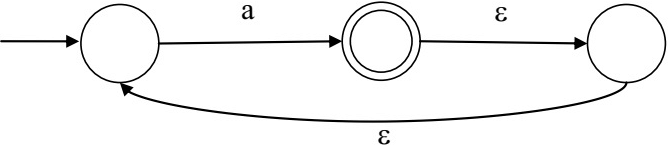
(a) ϕ
(b) {ε}
(c) a∗
(d) {a,ε}
Ans: (b)
Sol:
Language being accepted by this NFA is : a+
complement of language = (Σ* - a+) = (a* - a+)
a* ={ϵ,a,aa,aaa,....}
a+ ={a,aa,aaa,......}
so, complement of language = {ϵ}
Q24: A deterministic finite automation (DFA)D with alphabet ∑ = {a, b} is given below 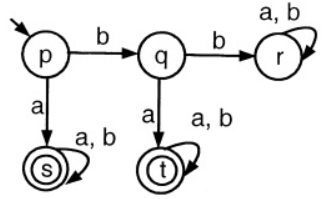
Which of the following finite state machines is a valid minimal DFA which accepts the same language as D? (2011)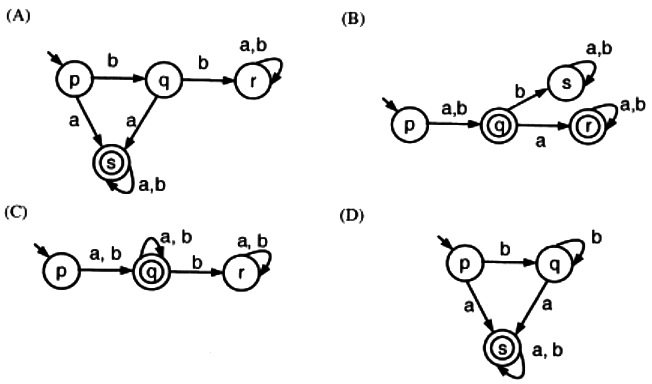
(a) A
(b) B
(c) C
(d) D
Ans: (a)
Sol:
In (B) and (C) when the first letter of input is 'b' we reach final state, while in the given DFA first letter 'b' is not a final state. So, (B) and (C) are not accepting same language as the given DFA.
In (D) we can reach final state when the last letter is 'a', whatever be the previous transitions. But in the given DFA, when the first 2 letters are 'b' we can never reach the final state. So, (D) is also accepting a different language than the given DFA.
Q25: Definition of a language L with alphabet (a) is given as following
L = {ank | k > 0, and n is a positive integer constant}
What is the minimum number of states needed in a DFA to recognize L? (2011)
(a) k + 1
(b) n + 1
(c) 2n+1
(d) 2k+1
Ans: (b)
Sol:
(B) n + 1
We need a state for strings of length 0, 1, 2,... n (and their respective multiples with k). Each of these set of strings form an equivalence class as per Myhill-Nerode relation and hence needs a separate state in min-DFA.
One thing to notice here is k > 0. Because of this we are not able to combine Class 1 and Class n + 1. Had it been k ≥ 0, we would have had only n equivalent classes and equivalently n states in the minimal DFA.
Q26: Which of the following pairs have DIFFERENT expressive power? (2011)
(a) Deterministic finite automata (DFA) and Non-deterministic finite automata (NFA)
(b) Deterministic push down automata (DPDA) and Non-deterministic push down automata (NPDA)
(c) Deterministic single-tape Turing machine and Non-deterministic single tape Turing machine
(d) Single-tape Turing machine and multi-tape Turing machine
Ans: (b)
Sol:
Expressing power of any machine can be defined as the maximum number of languages it can accept..if machine M1 can accept more languages then M2 then we can say that expressing power of M1 is greater then M2.
A. Languages accepted by NFA, will also be accepted by DFA because we can make DFA corresponding to NFA. So their expressing power is same.
B. In this case languages accepted by NPDA is more then DPDA, so expressing power of NPDA is more then DPDA
C. Both deterministic and non deterministic turing can accept same language.so there expressing power is same.
D. In turing machine if we increase the number of tape then also language accepted by that machine is same as single tape turing machine.so there expressing power is same.
Answer is B.
Q27: Let w be any string of length n in {0, 1}*. Let L be the set of all substrings of w. What is the minimum number of states in a non-deterministic finite automaton that accepts L? (2010)
(a) n - 1
(b) n
(c) n + 1
(d) 2n-1
Ans: (c)
Sol:
Suppose a string w from (0 + 1)* is 001 {n = 3}
Step1. Draw a NFA that accept 001 so it requires (n + 1 = 4) states
step2. Now our requirement is to draw a NFA for "L be the set of all substrings of w". so From NFA given in
step1 attach an branch containing ε from initial state to all other states. This ε-NFA accepts L.
but there may be a confusion that it is a ε-NFA as i know that for an ε-NFA an equivalent NFA(w/o ε)
contains same no of states as in ε-NFA
Hence this NFA also contains "n + 1" states
Step3. now someone ask that how many minimum states DFA it requires to accept the L so i want to tell u that there is no any standard result for it and also it is wrong to say that DFA for L contains "n + 2" states it is variying {u can check it also by taking some examples).
|
18 videos|70 docs|44 tests
|
FAQs on Previous Year Questions: Finite Automata - Theory of Computation - Computer Science Engineering (CSE)
| 1. What is a finite automaton in computer science? |  |
| 2. How does a finite automaton work? |  |
| 3. What is the difference between a deterministic finite automaton (DFA) and a non-deterministic finite automaton (NFA)? |  |
| 4. Can a finite automaton recognize regular languages? |  |
| 5. What are some applications of finite automata in computer science? |  |






















