NEET Previous Year Questions (2014-2025): Work, Energy & Power | Physics Class 11 PDF Download
The terms ‘work’, ‘energy’, and ‘power’ are frequently used in everyday language. In physics, however, the word ‘Work’ covers a definite and precise meaning. This chapter of NEET physics covers the fundamental concepts of energy, work, and power, and their applications to various physical systems. Let's have a look at the Previous Year's Questions of NEET Exam of this chapter.

2025
Q1: The kinetic energies of two similar cars A and B are 100 J and 225 J respectively. On applying breaks, car A stops after 1000 m and car B stops after 1500 m. If FA and FB are the forces applied by the breaks on cars A and B, respectively, then the ratio FA / FB is: [2025]
(a) 1/3
(b) 1/2
(c) 3/2
(d) 2/3
Ans: (d)
From work energy theorm
W . D = ΔKE
⇒ F . S = ΔKE
⇒ (ΔKE)A / (ΔKE)B = - FA SA / FB SB
⇒ (-100) / (225) = - FA(1000) / FB(1500)
FA / FB = 2 / 3
Q2: A bob of heavy mass m is suspended by a light string of length l. The bob is given a horizontal velocity v0 as shown in figure. If the string gets slack at some point P making an angle θ from the horizontal, the ratio of the speed v of the bob at point P to its initial speed v0 is: [2025]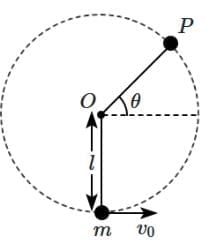 (a)
(a) 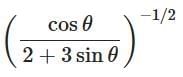
(b) 
(c) 
(d) 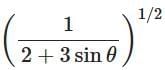
Ans: (b)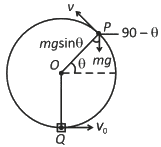
At Point P, mg sin θ = m v2/ l ... (1)
By conservation of mechanical energy at point P ∈ Q
(1/2) mv02 = (1/2) mv2 + mg (I + I sin θ)
⇒ v02 / 2 = v2 / 2 + gl(1 + sin θ)
Put gl = v2 / l sin θ using (1)
v02 / 2 = v2 / 2 + (v2 / sin θ)(1 + sin θ)
v02 / 2 = (3v2/2) + (v2 / sin θ)
⇒v / v0 = (sin θ /(2 + 3 sin θ))1/2
2024
Q1: At any instant of time t, the displacement of any particle is given by 2t − 1 (SI unit) under the influence of force of 5N. The value of instantaneous power is (in SI unit):
(a) 10
(b) 5
(c) 7
(d) 6
Ans: (a)
To find the instantaneous power delivered by a force, we can use the formula:
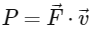
where P is the power,  is the force vector, and
is the force vector, and  is the velocity vector of the particle.
is the velocity vector of the particle.
In this question, the force exerted is given as a constant 5N. Since no direction is specified, and the displacement is given in a scalar form, we assume the force acts along the direction of displacement. Therefore, we can treat the vectors as scalars for simplicity.
The displacement of the particle is given by:
The velocity, 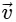 , is the derivative of displacement with respect to time. Deriving the displacement equation with respect to time t gives:
, is the derivative of displacement with respect to time. Deriving the displacement equation with respect to time t gives: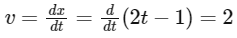
The instantaneous power can now be calculated as: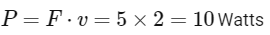
Thus, the instantaneous power delivered by the force at any time t is 10 Watts
The correct answer is Option A: 10.
Q2: Two bodies A and B of same mass undergo completely inelastic one dimensional collision. The body A moves with velocity v1 while body B is at rest before collision. The velocity of the system after collision is v2. The ratio v1 : v2 is: [2024]
(a) 1 : 2
(b) 2 : 1
(c) 4 : 1
(d) 1 : 4
Ans: (b)
In a completely inelastic collision, the two bodies stick together and move with a common final velocity. Here, before the collision, body A is moving with a velocity v1 and body B is at rest. The conservation of momentum must hold true because no external forces are acting on the system.
The momentum before the collision is only due to body A since body B is at rest. Therefore, the total initial momentum p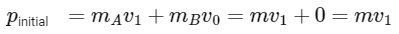
where:
- mA and mB are the masses of bodies A and B respectively,
- m is the mass of each body,
- v1 is the velocity of body A,
v0 = 0 is the velocity of body
Since they undergo a completely inelastic collision, bodies A and B stick together after the collision and hence move with a common velocity v2. The total mass of the combined system post-collision is  The momentum after the collision is given by:
The momentum after the collision is given by: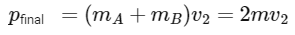
Applying the conservation of momentum (since no external force implies momentum is conserved), we equate p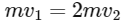
Dividing through by 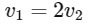
Thus, solving for the ratio v1 / v2 gives: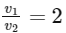
Therefore, the ratio of v1 to v2 is
Option B: 2 : 1
2023
Q1: The potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm, potential energy stored in it will be [2023](a) 2 U
(b) 4 U
(c) 8 U
(d) 16 U
Ans: d
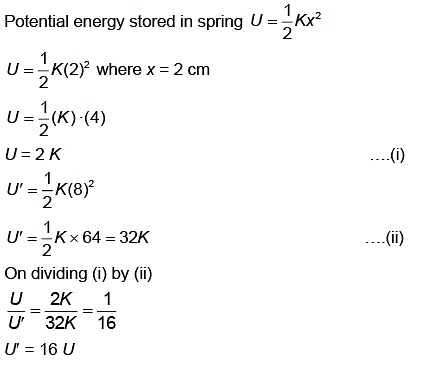
Q2: A particle moves with a velocity 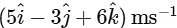 horizontally under the action of constant force
horizontally under the action of constant force  . The instantaneous power supplied to the particle is : [2023]
. The instantaneous power supplied to the particle is : [2023]
(a) 200 W
(b) Zero
(c) 100 W
(d) 140 W
Ans: (d)
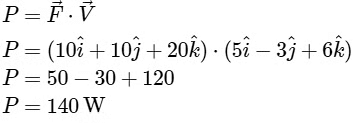
2022
Q1: The restoring force of a spring with a block attached to the free end of the spring is represented by [2022]
(a) 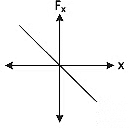
(b) 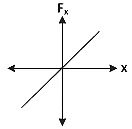
(c) 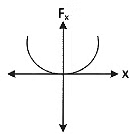
(d) 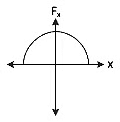
Ans: (a)
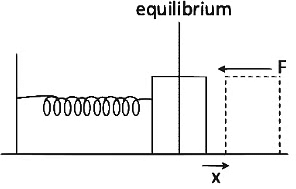
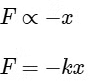
Where F is restoring force
x is displacement of block from equilibrium position

Q2: An electric lift with a maximum load of 2000 kg (lift + passengers) is moving up with a constant speed of 1.5 ms–1 . The frictional force opposing the motion is 3000 N. The minimum power delivered by the motor to the lift in watts is : (g = 10 m s –2 ) [2022]
(a) 20000
(b) 34500
(c) 23500
(d) 23000
Ans: b
The power delivered by the motor to the lift can be calculated using the formula:
Power = Force x Velocity
In this case, the force is the sum of the weight of the lift and the passengers and the frictional force opposing the motion:
Force = (Weight of lift + passengers) + Frictional force
Weight of lift + passengers = Mass x gravity
= (2000 kg / 1000) x 10 m/s2
= 20,000 N
Therefore,
Force = (20,000 N) + (3000 N)
= 23,000 N
Now, using the formula for power, we get:
Power = Force x Velocity
= (23,000 N) x (1.5 m/s)
= 34,500 W
Therefore, the minimum power delivered by the motor to the lift in watts is 34,500 W.
Q3: The energy that will be ideally radiated by a 100 kW transmitter in 1 hour is [2022]
(a) 36
(b) 36
(c) 36
(d) 1
Ans: (a)
Energy = Power
E = 100
= 36
2021
Q1: A particle is released from height S from the surface of the earth. At a certain height, its kinetic energy is three times its potential energy. The height from the surface of the earth and the speed of the particle at that instant are respectively: [2021]
(a) 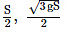
(b) 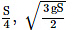
(c) 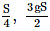
(d) 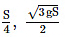
Ans: B
U + KE = E
4U = E = mgS
4mgh = mgS
h = S/4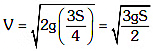
Q2: Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional force are 10% of the input energy. How much power is generated by the turbine?(g = 10 m/s2) [2021]
(a) 12.3 kW
(b) 7.0 kW
(c) 10.2 kW
(d) 8.1 kW
Ans: D
Mass of water falling/second = 15 kg/s h = 60 m, g = 10 m/s2, loss = 10 % i.e., 90% is used. Power generated = 15 x 10 x 60 x 0.9 = 8100 W = 8.1 kW.
2020
Q.6. The energy required to break one bond in DNA is 10–20J. This value in eV is nearly: [2020]
(a) 0.06
(b) 0.006
(c) 6
(d) 0.6
Ans: a
1.6 × 10–19 Joule = 1 eV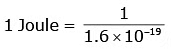
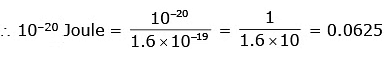
2019
Q1: A force F = 20 + 10 y acts on a particle in y direction where F is in newton and y in meter. Work done by this force to move the particle from y = 0 to y = 1 m is [2019]
(a) 30 J
(b) 5 J
(c) 25 J
(d) 20 J
Ans: c
Work done by variable force is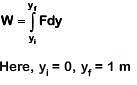
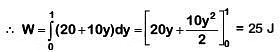
Q2: Body A of mass 4m moving with speed u collides with another body B of mass 2m, at rest. The collision is head on and elastic in nature. After the collision the fraction of energy lost by the colliding body A is: [2019]
(a) 1/9
(b) 8/9
(c) 4/9
(d) 5/9
Ans: b
Fractional loss of KE of colliding body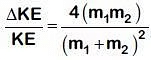
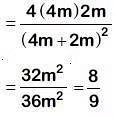
Q3: A disc of radius 2 m and mass 100 kg rolls on a horizontal floor. Its centre of mass has speed of 20 cm/s. How much work is needed to stop it? [2019]
(a) 3 J
(b) 30 kJ
(c) 2 J
(d) 1 J
Ans: a
Work required = change in kinetic energy Final KE = 0
Initial KE 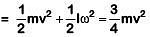
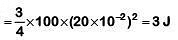
|ΔKE| = 3 J
Q4: The work done to raise a mass m from the surface of the earth to a height h, which is equal to the radius of the earth, is: [2019]
(a) mgR
(b) 2mgR
(c)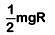
(d)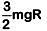
Ans: c
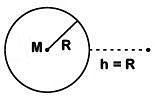
Initial potential energy at earths surface is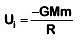
Final potential energy at height h = R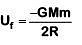
As work done = Change in PE∴ W = Uf – Ui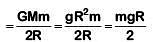
(∵ GM = gR2)
2018
Q1: A body initially at rest and sliding along a frictionless track from a height h (as shown in the figure) just completes a vertical circle of diameter AB = D. The height h is equal to [2018]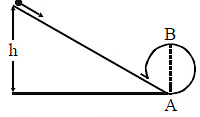 (a) 3/2 D
(a) 3/2 D
(b) D
(c) 7/5 D
(d) 5/4 D
Ans: d
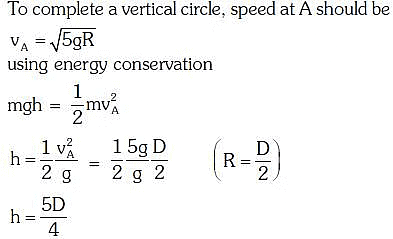
Q2: A moving block having mass m, collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the lighter block is v, then the value of coefficient of restitution (e) will be :- [2018]
(a) 0.5
(b) 0.25
(c) 0.8
(d) 0.4
Ans: b
Q3: The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are KA, KB and KC respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then [2018]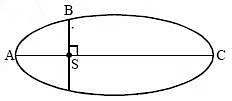 (a) KA < KB < KC
(a) KA < KB < KC
(b) KA > KB > KC
(c) KB < KA < KC
(d) KB > KA > KC
Ans: b
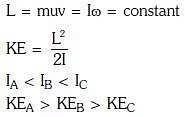
2017
Q1: Consider a drop of rain water having mass 1 g falling from a height of 1 km. It hits the ground with a speed of 50 m/s. Take 'g' constant with a value 10 m/s2. The work done by the [2017]
(i) gravitational force and the
(ii) resistive force of air is :-
(a) (i) 1.25 J (ii) – 8.25 J
(b) (i) 100 J (ii) 8.75 J
(c) (i) 10 J (ii) – 8.75 J
(d) (i) – 10 J (ii) – 8.25 J
Ans: c
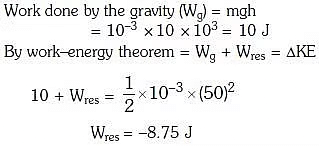
Q2: A spring of force constant k is cut into lengths of ratio 1: 2 : 3. They are connected in series and the new force constant is k'. Then they are connected in parallel and force constant is k''. Then k' : k'' is [2017]
(a) 1 : 6
(b) 1 : 9
(c) 1 : 11
(d) 1 : 14
Ans: c
Force constant of spring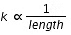
after cutting the spring in the ratio 1:2:3, the force constants will be in the ratio 6:3:2
Force constant in series K' is given by 
Force constant in parallel K" : 6k+3k+2k = 11k;hence K'/K" = 1/11
2016
Q1: A particle moves from a point 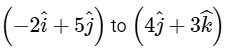 when a force of
when a force of 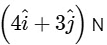 N is applied. How much work has been done by the force ? [2016]
N is applied. How much work has been done by the force ? [2016]
(a) 8 J
(b) 11 J
(c) 5 J
(d) 2 J
Ans: (c)
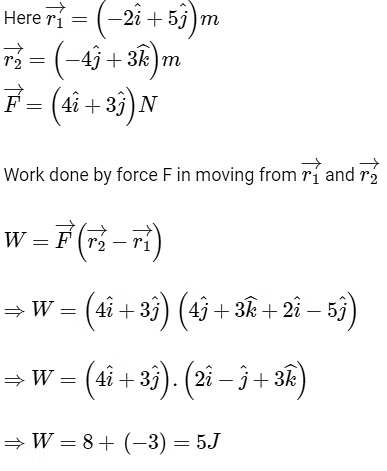
Q2: A body of mass 1 kg begins to move under the action of a time dependent force 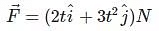 , when
, when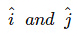 are unit vectors along x and y axis. What power will be developed by the force at the time t ? [2016]
are unit vectors along x and y axis. What power will be developed by the force at the time t ? [2016]
(a) (2t3+ 3t5)W
(b) (2t2 + 3t3)W
(c) (2t2 + 4t4)W
(d) (2t3 + 3t4)W
Ans: a
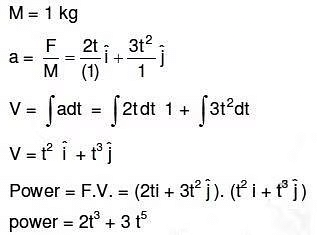
Q3: A particle of mass 10 g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal to 8 × 10−4 J by the end of the second revoluation after the beginning of the motion ? [2016]
(a) 0.18 m/s2
(b) 0.2 m/s2
(c) 0.1 m/s2
(d) 0.15 m/s2
Ans: (c)
Given: Mass of particle, M = 10g
radius of circle R = 6.4 cm
Kinetic energy E of particle = 8 × 10–4J
acceleration at = ?

Now, using

Q4: What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
Ans: (b)
To complete the loop a body must enter a vertical loop of radius R with the minimum velocity v =√5gR
2015
Q1: Two particles A and B, move with constant velocities 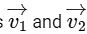 . At the initial moment their position vectors are
. At the initial moment their position vectors are 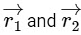 respectively. The condition for particles A and B for their collision is [2015]
respectively. The condition for particles A and B for their collision is [2015]
(a) 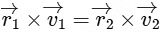
(b) 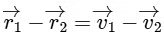
(c) 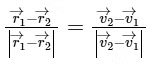
(d) 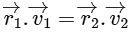 Ans: (c)
Ans: (c)
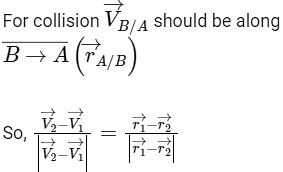
Q2: A ball is thrown vertically downwards from a height of 20 m with an initial velocity v0. It collides with the ground, losses 50 percent of its energy in collision and rebounds to the same height. The initial velocity v0 is (Take g = 10 m s−2) [2015]
(a) 28 m s−1
(b) 10 m s−1
(c) 14 m s−1
(d) 20 m s−1
Ans: (d)
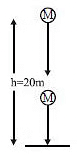
When ball collides with the ground it loses its 50% of energy
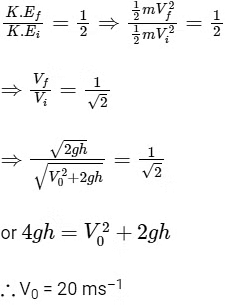
Q3: The heart of a man pumps 5 litres of blood through the arteries per minute at a pressure of 150 mm of mercury. If the density of mercury be 13.6 × 103 kg/m3 and g = 10 m/s2 then the power (in watt) is [2015]
(a) 3.0
(b) 1.50
(c) 1.70
(d) 2.35
Ans: (c)
Here, Volume of blood pumped by man’s heart,
V = 5 litres = 5 × 10–3 m3 (
Time in which this volume of blood pumps, t = 1 min = 60 s
Pressure at which the blood pumps,
P = 150 mm of Hg = 0.15 m of Hg
= (0.15 m)(13.6 × 103 kg/m3)(10 m/s2)
= 20.4 × 103 N/m2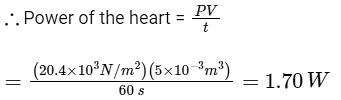
Q4: Two particles of masses m1, m2 move with initial velocities u1 and u2. On collision, one of the particles get excited to higher level, after absorbing energy ε. If final velocities of particles be v1 and v2 then we must have : [2015]
(a) 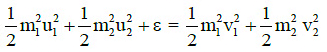
(b)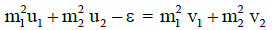
(c) 
(d) 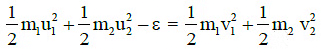
Ans: d
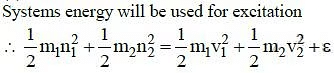
Q5: Two similar springs P and Q have spring constants KP and KQ, such that KP > KQ. They are stretched, first by the same amount (case a), then by the same force (case b). The work done by the springs WP and WQ are related as, in case (a) and case (b), respectively: [2015]
A: WP < WQ; WQ < WP
B: WP = WQ; WP > WQ
C: WP = WQ; WP = WQ
D: WP > WQ; WQ > WP
Ans: d

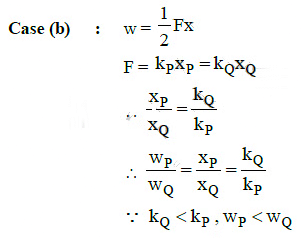
Q6: A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to a string which passes through a smooth hole in the plane as shown.
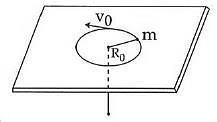
The tension in the string is increased gradually and finally m moves in a circle of radius R0/2. The final value of the kinetic energy is : [2015]
(a)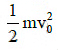
(b) 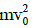
(c)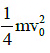
(d)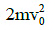
Ans: d
When a mass moves in a circle of radius R0 with velocity v0, its kinetic energy is given by The tension in the string is gradually increased and the radius of the circle decreased to R0/2. When the radius of the circle is R
The tension in the string is gradually increased and the radius of the circle decreased to R0/2. When the radius of the circle is R 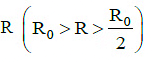 the tension in the string is the same as the centripetal force.
the tension in the string is the same as the centripetal force.
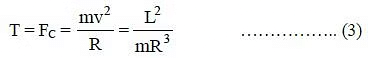 where L = mRv is the angular momentum which is conserved.Work done in reducing the radius of the circle from R0 to R0/2 is
where L = mRv is the angular momentum which is conserved.Work done in reducing the radius of the circle from R0 to R0/2 is
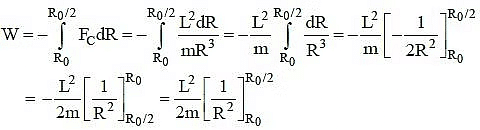
(a) 250 J
(b) 475 J
(c) 450 J
(d) 275 J
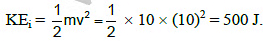 It is subjected to a retarding force F = 0.1 x J/m during its travel from x = 20 m to 30 m.Work done is given by
It is subjected to a retarding force F = 0.1 x J/m during its travel from x = 20 m to 30 m.Work done is given by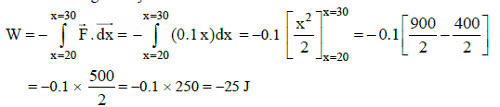 Final kinetic energy is, KEf = KEi + W = 500 - 25 = 475
Final kinetic energy is, KEf = KEi + W = 500 - 25 = 475|
96 videos|367 docs|98 tests
|
FAQs on NEET Previous Year Questions (2014-2025): Work, Energy & Power - Physics Class 11
| 1. What is work in the context of physics? |  |
| 2. How is energy related to work? |  |
| 3. What is power in the context of physics? |  |
| 4. How can the concept of work, energy, and power be applied in real-life situations? |  |
| 5. How can one increase the power output in a mechanical system? |  |






















