NEET Previous year questions (2014-2024): System of Particles & Rotational Motion | Physics Class 11 PDF Download
2024
Q1: The moment of inertia of a thin rod about an axis passing through its mid point and perpendicular to the rod is 2400gcm2. The length of the 400g rod is nearly: [2024](a) 8.5 cm
(b) 17.5 cm
(c) 20.7 cm
(d) 72.0 cm
Ans: (a) 8.5 cm
Explanation:
Moment of Inertia of rod =
Q2: A wheel of a bullock cart is rolling on a level road as shown in the figure below. If its linear speed is v in the direction shown, which one of the following options is correct (P and Q are any highest and lowest points on the wheel, respectively)? [2024] (a) Point P moves slower than point Q
(a) Point P moves slower than point Q
(b) Point P moves faster than point Q
(c) Both the points P and Q move with equal speed
(d) Point P has zero speed
Ans: (b) Point P moves faster than point Q
Explanation:
In the case of pure rolling,
The linear speed of the centre of the wheel is Q are the highest and lowest points on the wheel, respectively.
For rolling motion, every point on the wheel has two components of velocity:
- The translational velocity due to the movement of the entire wheel (
- The rotational velocity due to the wheel spinning. The velocity of a point on the rim is R is the radius of the wheel).
- For the topmost point (P):
(i) The translational velocity is
(ii) The rotational velocity at v (forward direction, since it rotates along with the wheel).
(iii) So, the total velocity of- For the bottommost point (Q):
(i) The translational velocity is v (forward).
(ii) The rotational velocity at v (backward direction, because it rotates in the opposite direction of translational motion).
(iii) So, the total velocity at
2023
Q1: The ratio of radius of gyration of a solid sphere of mass M and radius R about its own axis to the radius of gyration of the thin hollow sphere of same mass and radius about its axis is [2023](a) 3 : 5
(b) 5 : 3
(c) 2 : 5
(d) 5 : 2
Ans: (a) 3 : 5
Explanation:
The moment of inertia of a body about a given axis is related to the radius of gyration by the equation:
Where:
- = Moment of inertia
- = Mass of the body
- = Radius of gyration
For a solid sphere rotating about its own axis, the moment of inertia is given by:
For a thin hollow sphere rotating about its own axis, the moment of inertia is given by:
Now, we take the ratio of the radius of gyration of the solid sphere to the hollow sphere:
Q2: The angular acceleration of a body, moving along the circumference of a circle, is :
(a) along the radius towards the centre
(b) along the tangent to its position
(c) along the axis of rotation
(d) along the radius, away from centre [2023]
Ans: (c) along the axis of rotation
Explanation:
Angular acceleration refers to the rate of change of angular velocity of a body moving in a circular path. Angular acceleration is a vector quantity, and its direction depends on the direction of the change in angular velocity.
When a body moves along the circumference of a circle, its angular acceleration is associated with the axis of rotation, which is perpendicular to the plane of motion.
The direction of angular acceleration is the same as the direction of the change in angular velocity. For rotational motion, the axis of rotation determines the orientation of angular velocity and angular acceleration.
2022
Q1: An energy of 484 J is spent in increasing the speed of a flywheel from 60 rpm to 360 rpm. The moment of inertia of the flywheel is
(a) 0.07 kg-m2
(b) 0.7 kg-m2
(c) 3.22 kg-m2
(c) 30.8 kg-m2
Ans: (b) 0.7 kg-m2
Explanation:
Given:Energy spent J
Initial angular speed
Final angular speed
2. The change in rotational kinetic energy is given by:
3. Substitute the known values into the equation:
Q2: The angular speed of a fly wheel moving with uniform angular acceleration changes from 1200 rpm to 3120 rpm in 16 seconds. The angular acceleration in rad/s2 is [2022]
(a) 2π
(b) 4π
(c) 12π
(d) 104π
Ans: (b) 4π
Explanation:Given:
Initial angular speed,
Final angular speed,
Time interval,
Angular acceleration α is given by the formula:
Q3: Two objects of mass 10 kg and 20 kg respectively are connected to the two ends of a rigid rod of length 10 m with negligible mass. The distance of the center of mass of the system from the 10 kg mass is [2022]
(a) 20/3 m
(b) 10 m
(c) 5 m
(d) 10/3 m
Ans: (a) 20/3 m
Explanation:
Given:Mass of the first object,
Mass of the second object, kg
Length of the rod, m
We need to find the distance of the center of mass from the 10 kg mass.

Q4: The ratio of the radius of gyration of a thin uniform disc about an axis passing through its center and normal to its plane to the radius of gyration of the disc about its diameter is [2022]
(a) √2: 1
(b) 4: 1
(c) 1: √2
(d) 2: 1
Ans: (a) √2: 1
Explanation:
Now, we take the ratio of the radius of gyration about the center to that about the diameter:
2021
Q1: From a circular ring of mass 'M' and radius 'R' an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is 'K' times 'MR2'. Then the value of 'K' is : [2021]
(a) 1/4
(b) 1/8
(c) 3/4
(d) 7/8
Ans: (c) 3/4
Explanation:
The moment of inertia of a full circular ring about its center and perpendicular to the plane is:
Since a 90° sector is removed, this represents of the total mass of the ring. The mass of the removed sector is:
The moment of inertia of the removed sector is proportional to its mass, so:
Now,
The moment of inertia of the remaining part is given as K×MR2, so:
Q2: A uniform rod of length 200 cm and mass 500 g is balanced on a wedge placed at 40 cm mark. A mass of 2 kg is suspended from the rod at 20 cm and another unknown mass 'm' is suspended from the rod at 160 cm mark as shown in the figure. Find the value of 'm' such that the rod is in equilibrium. (g=10 m/s2) [2021]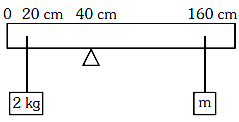
(a) 1/6 kg
(b) 1/12 kg
(c) 1/2 kg
(d) 1/3 kg
Ans: (b) 1/12 Kg
Explanation:Given:
Length of the rod = 200 cmMass of the rod = 500 g = 0.5 kg
The rod is balanced at the 40 cm mark.
A mass of 2 kg is suspended at the 20 cm mark.
An unknown mass m is suspended at the 160 cm mark.
The rod is in equilibrium, and the acceleration due to gravity
Torque due to the 2 kg mass at 20 cm:
The distance from the pivot (40 cm) to the 2 kg mass (at 20 cm) is:
20cm = 0.2m
Torque due to this mass (T1) is:
4Nm
This torque is clockwise.
Torque due to the unknown mass m at 160 cm:
The distance from the pivot (40 cm) to the unknown mass m (at 160 cm) is:
= 1.2m
Torque due to this mass (T2) is:
m Nm
This torque is counterclockwise.
Torque due to the mass of the rod:
The rod's mass acts at its center of mass, which is at the midpoint of the rod (100 cm).
The distance from the pivot (40 cm) to the center of mass (100 cm) is:
0.6 m
Torque due to the rod's mass (T3) is:
T3 = 0.5 × g × 0.6 = 03Nm
This torque is counterclockwise.
Equilibrium Condition (Net Torque = 0):The sum of clockwise and counterclockwise torques must balance:
T1= T2 + T3
Substituting the values:
Solving for m:
4−3=12m
2020
Q1: Find the torque about the origin when a force of acts on a particle whose position vector is
acts on a particle whose position vector is  [2020]
[2020]
(a) 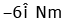
(b) 
(c) 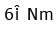
(d) 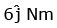
Ans: (a) 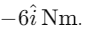
Explanation:
Given:
Q2: Two particles of mass 5kg and 10 kg respectively are attached to the two ends of a rigid rod of length 1m with negligible mass. The centre of mass of the system from the 5kg particle is nearly at a distance of: [2020]
(a) 67 cm
(b) 80 cm
(c) 33 cm
(d) 50 cm
Ans: (a) 67 cm
Explanation:
Given:Mass of the first particle, 5kg
Mass of the second particle, 10kg
Length of the rod, 1m =100cm
We need to find the distance of the center of mass from the 5 kg particle.
2019
Q1: A solid cylinder of mass 2 kg and radius 4 cm is rotating about its axis at the rate of 3 rpm. The torque required to stop after 2π revolutions is [2019]
(a) 2 × 10-6 N m
(b) 2 × 10-3 N m
(c) 12 × 10-4 N m
(d) 2 × 106 N m
Ans: (a) 2 × 10-6 N m
Explanation:
We take only magnitude, therefore,
Q2: Two particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed vA and vB respectively. Their time period of rotation is the same. The ratio of angular speed of A to that of B will be: [2019]
(a) rA : rB
(b) vA : vB
(c) rB : rA
(d) 1 : 1
Ans: (d) 1 : 1
Explanation:
Q3: A disc of radius 2 m and mass 100 kg rolls on a horizontal floor. Its centre of mass has speed of 20 cm/s. How much work is needed to stop it? [2019]
(a) 1 J
(b) 2 J
(c) 3 J
(d) 30 J
Ans: (c) 3 J
Explanation:
Given:Radius of the disc, 2 m
Mass of the disc, 100 kg
Speed of the center of mass, 20 cm/s = 0.2m/s
We need to find the work required to stop the disc.
When the disc is rolling on a horizontal surface, it has both translational kinetic energy and rotational kinetic energy.
For a solid disc, the moment of inertia about its axis is:
2018
Q1: Three objects, A : (a solid sphere), B : (a thin circular disk) and C = (a circular ring), each have the same mass M and radius R. They all spin with the same angular speed ω about their own symmetry axes. The amounts of work (W) required to bring them to rest, would satisfy the relation:- [2018]
(a) WC > WB > WA
(b) WA > WB > WC
(c) WB > WA > WC
(d) WB > WA > WC
Ans: (a) WC > WB > WA
Explanation:
Q2: The moment of the force,  at (2, 0, –3), about the point (2, –2, –2), is given by:- [2018]
at (2, 0, –3), about the point (2, –2, –2), is given by:- [2018]
(a) 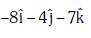
(b) 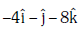
(c) 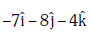
(d) 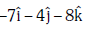
Ans: (d) 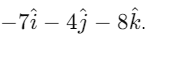
Explanation:
Q3: A solid sphere is in rolling motion. In rolling motion a body possesses translational kinetic energy (Kt) as well as rotational kinetic energy (Kr) simultaneously. The ratio Kt : (Kt + Kr) for the sphere is [2018]
(a) 7 : 10
(b) 5 : 7
(c) 10 : 7
(d) 2 : 5
Ans: (b) 5 : 7
Explanation:
Given:
Q4: A solid sphere is rotating freely about its symmetry axis in free space. The radius of the sphere is increased keeping its mass same. Which of the following physical quantities would remain constant for the sphere ? [2018]
(a) Angular velocity
(b) Moment of inertia
(c) Rotational kinetic energy
(d) Angular momentum
Ans: (d) Angular Momentum
Explanation:
(a) Angular momentum (L): In free space, no external torque acts on the sphere, so angular momentum remains conserved (as per the law of conservation of angular momentum). Angular momentum is given by:Where:
I is the moment of inertia.
ω is the angular velocity.
Since no external torque is acting, angular momentum remains constant.
(b) Moment of inertia (I): The moment of inertia of a solid sphere about its axis is given by:
Where:
M is the mass of the sphere.
R is the radius of the sphere.
As the radius
(d) Rotational kinetic energy (K):The rotational kinetic energy is given by:
K = 1 2 I ω 2 K = \frac{1}{2} I \omega^2As
I increases and ω decreases, the rotational kinetic energy will change (decrease) because both \omega I and I ω are changing in opposite directions. \omega
2017
Q1: A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? [2017]
(a) 0.25 rad/s2
(b) 25 rad/s2
(c) 5 m/s2
(d) 25 m/s2
Ans: (b) 25 rad/s2
Explanation:
Given:
Mass of the hollow cylinder,
M =3 kg kgM = 3 \, \text{kg} Radius of the cylinder,
mR = 40 \, \text{cm} = 0.4 \, \text{m} R = 40 cm = 0.4 mForce applied on the rope, F = 30 N
We need to find the angular acceleration α of the cylinder.
\alpha The moment of inertia I of a hollow cylinder about its axis is:
The angular acceleration is related to torque and moment of inertia by the equation:
Q2: Two discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is:- [2017]
(a) 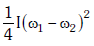
(b)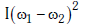
(c) 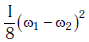
(d) 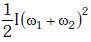
Ans: (a) 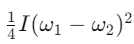
Explanation:
The initial kinetic energy of the system (both discs) before being brought into contact is:
When the two discs are brought into contact and rotate together, the total angular momentum is conserved. Therefore:
After the discs are brought into contact, the final kinetic energy of the system is:
The energy lost during the process is the difference between the initial and final kinetic energies:
Q3: Which of the following statements are correct ? [2017]
(a) Centre of mass of a body always coincides with the centre of gravity of the body
(b) Central of mass of a body is the point at which the total gravitational torque on the body is zero
(c) A couple on a body produces both translational and rotation motion in a body
(d) Mechanical advantage greater than one means that small effort can be used to lift a large load
(a) (a) and (b)
(b) (b) and (c)
(c) (c) and (d)
(d) (b) and (d)
Ans: (d) (b) and (d)
Explanation:
(a) Centre of mass of a body always coincides with the centre of gravity of the body:False: The center of mass and the center of gravity coincide only in a uniform gravitational field. In non-uniform fields, they may not coincide because the center of gravity depends on the distribution of gravitational forces.
(b) Centre of mass of a body is the point at which the total gravitational torque on the body is zero:
True: The center of mass is the point where all the mass of the body can be considered to be concentrated, and the total gravitational torque about this point is zero.
(c) A couple on a body produces both translational and rotational motion in a body:
False: A couple consists of two equal and opposite forces whose lines of action do not coincide. A couple produces only rotational motion without any translational motion, as the net force is zero but the net torque is not.
(d) Mechanical advantage greater than one means that small effort can be used to lift a large load:
True: Mechanical advantage (MA) is the ratio of load to effort. When MA is greater than 1, a small effort is sufficient to lift a large load, making it easier to perform the task.
Conclusion:
(b) is true because the center of mass is the point where the total gravitational torque is zero.
(d) is true because mechanical advantage greater than 1 means a small effort can lift a large load.
2016
Q1: From a disc of radius R and mass M1 a circular hole of diameter R1 whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about at perpendicular axis, passing through the centre ? [2016]
(a) 9MR2/32
(b) 15MR2/32
(c) 13MR2/32
(d) 11 MR2/32
Ans: (c) 3MR2/32
Explanation:
Option C is correct Answer.
Q2: A disk and a sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first ? [2016]
(a) Depends on their masses
(b) Disk
(c) Sphere
(d) both reach at the same time
Ans: (c) Sphere
Explanation:
When a disk and a sphere roll down an inclined plane, the speed at which they reach the bottom depends on the distribution of mass in relation to their rotation. This is determined by their moment of inertia and how it affects their total kinetic energy.
Q3: A uniform circular disc of radius 50 cm at rest is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of 2.0 rad s-2. Its net acceleration in ms-2 at the end of 2.0 s is approximately : [2016]
(a) 3.0
(b) 8.0
(c) 7.0
(d) 6.0
Ans: (b) 8.0
Explanation:
The angular speed of disc increases with time, and hence centripetal acceleration also increases.
Q4: A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is [2016]
(a) 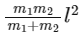
(b) 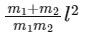
(c) 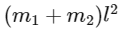
(d) 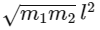
Ans: (a) 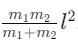
Explanation:
Q5: A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation (Esphere / Ecylinder) will be [2016]
(a) 2 : 3
(b) 1 : 5
(c) 1 : 4
(d) 3 : 1
Ans: (b) 1 : 5
Explanation:
2015
Q1: Three identical spherical shells, each of mass m and radius r are placed as shown in figure. Consider an axis XX' which is touching to two shells and passing through diameter of third shell. Moment of inertia of the system consisting of these three spherical shells about XX' axis is : [2015]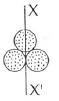
(a) 4 mr2
(b) 11/5 mr2
(c) 3 mr2
(d) 16/5 mr2
Ans: (a) 4 mr2
Explanation:
Similarly the moment of inertia of the spherical shell C about the XX' axis is
Q2: A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is [2015]
(a) 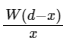
(b) 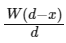
(c) 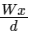
(d) 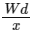
Ans: (b) 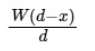
Explanation:
Given situation is shown in figure.
N1 = Normal reaction on A
N2 = Normal reaction on B
W = Weight of the rod
In vertical equilibrium,
N1 + N2 = W …(i)
Torque balance about centre of mass of the rod,
N1x = N2(d – x)
Putting value of N2 from equation (i)
N1x = (W – N1)(d – x)N1x = Wd – Wx – N1d + N1x ⇒ N1d = W(d – x) ⇒
Q3: Three identical spherical shells, each of mass m and radius r are placed as shown in figure. Consider an axis XX' which is touching to two shells and passing through diameter of third shell. Moment of inertia of the system consisting of these three spherical shells about XX' axis is [2015]
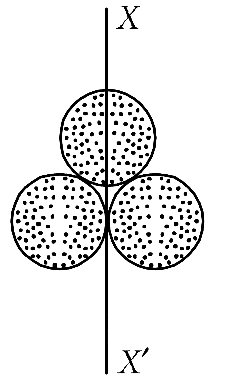
(a) 16/5mr2
(b) 4mr2
(c) 11/5mr2
(d) 3mr2
Ans: (b) 4mr2
Explanation:
Net moment of inertia of the system,
I = I1 + I2 + I3
The moment of inertia of a shell about its diameter,
Q4: An automobile moves on a road with a speed of 54 km h
(a) 10.86 kg m2 s
(b) 2.86 kg m2 s
(c) 6.66 kg m2 s
(d) 8.58 kg m2 s
Ans: (c) 6.66 kg m2 s
Explanation:
Here, Speed of the automobile,
Radius of the wheel of the automobile, R = 0.45 m
Moment of inertia of the wheel about its axis of rotation, I = 3 kg m2
Time in which the vehicle brought to rest, t = 15 s
The initial angular speed of the wheel is
Q5: A force  is acting at a point
is acting at a point  . The value of αfor which angular momentum about origin is conserved is [2015]
. The value of αfor which angular momentum about origin is conserved is [2015]
(a) Zero
(b) 1
(c) -1
(d) 2
Ans: (c) -1
Explanation:
From Newton's second law for rotational motion,
2014
Q1: A solid cylinder of mass 50 kg and radius 0.5 m is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of 2 revolutions s−2 is: [2014]
(a) 78.5 N
(b) 157 N
(c) 25 πN
(d) 50 N
Ans: (b) 157 N
Explanation:
Q2: The ratio of the accelerations for a solid sphere (mass ‘m’ and radius ‘R’) rolling down an incline of angle ‘θ’ without slipping and slipping down the incline without rolling is : [2014]
(a) 2 : 5
(b) 7 : 5
(c) 5 : 7
(d) 2 :3
Ans: (c) 5 :7
Explanation:
Q3: A body of mass (4m) is lying in x−y plane at rest. It suddenly explodes into three pieces. Two pieces, each of mass (m) move perpendicular to each other with equal speeds (ν). The total kinetic energy generated due to explosion is : [2014]
(a) 2 mν2
(b) 4 mν2
(c) mν2
(d) 3/2 mν2
Ans: (d) 3/2 mv2
Explanation:
|
97 videos|378 docs|103 tests
|
FAQs on NEET Previous year questions (2014-2024): System of Particles & Rotational Motion - Physics Class 11
| 1. What are the key concepts of System of Particles in NEET Physics? |  |
| 2. How do I calculate the center of mass for a system of particles? |  |
| 3. What is the importance of rotational motion in NEET exams? |  |
| 4. How do I solve problems related to torque and moment of inertia? |  |
| 5. What are some common types of questions asked in NEET regarding System of Particles and Rotational Motion? |  |

|
Explore Courses for NEET exam
|

|


 The linear speed of the centre of the wheel is Q are the highest and lowest points on the wheel, respectively.
The linear speed of the centre of the wheel is Q are the highest and lowest points on the wheel, respectively.






















































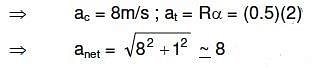





 Given situation is shown in figure.
Given situation is shown in figure.































