Profit & Loss | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
| Table of contents |

|
| Introduction |

|
| Definition |

|
| Important Formulae |

|
| Discount |

|
| Markup Price |

|
| Faulty Balance |

|
Introduction
Profit and Loss is a fundamental concept in business and finance that helps individuals and organizations assess the financial health of their operations. It involves understanding the difference between the revenue generated from selling goods or services and the costs incurred to produce or deliver them.
 Profit is the amount left after subtracting the expenses from the income. Loss occurs when the expenses exceed the income. This concept is crucial for making informed decisions about pricing, costs, and overall business strategies.
Profit is the amount left after subtracting the expenses from the income. Loss occurs when the expenses exceed the income. This concept is crucial for making informed decisions about pricing, costs, and overall business strategies.
Definition
To solve Profit and Loss questions, following are the terms that we should be aware of- Cost Price: C.P. is the price at which one buys anything.
- Selling Price: S.P. is the price at which one sells anything
- Profit/Loss: This is the difference between the selling price and the cost price. If the difference is positive it is called the profit and if negative it is called a loss.
- Profit/Loss %:This is the profit/loss as a percentage of the C.P.
- Margin: Normally is in % terms only. This is the profit as a percentage of S.P.
- Marked Price: This is the price of the product as displayed on the label.
- Discount:This is the reduction given on the marked price before selling it to a customer. If the trader
wants to make a loss he can offer a discount on the cost price as well - Markup: This is the increment on the cost price before being sold to a customer.
Important Formulae
- Gain = (S.P. - C.P.)
- Loss = (C.P. - S.P.)
- Gain % = (Gain × 100)/C. P
- Loss % = (Loss × 100)/C. P
- Given the cost & the gain percent,
S.P. = (100 + gain %) × C. P. / 100 - Given the cost & the loss percent,
S.P. = (100 - loss %) × C. P. / 100 - Given the M.P. & the discount,
C.P. = (100 - Discount %) x M.P / (100 + gain %) - Given the M.P. & the discount,
C.P. = (100. - Discount %) x M.P / (100 - loss %)
Example: A person sells 36 oranges for one rupee and suffers a loss of 4%. Find how many oranges per rupee to be sold to have a gain of 8%?
Sol. Let ‘X’ is the cost price of each orange.
Since he is giving 36 apples for one rupee, the selling price of an orange isrupee.
Since he got 4% loss, the selling price of each orange is 0.96X =
To get 8% gain he has to sell it for 1.08X=rupee.
So for one rupee, he has to give 32 oranges to get a gain of 8%.
Discount
- You always come across different offers attracting the customers such as “Buy 1 get 2 Free” or “Buy 3 get 5 Free” or “SALE 50% + 40%”. Can you calculate the discount offered to you?
- Most of us are not aware of the offer given to us. The percentage of the discount offered in the first case is not 200% but it is 66.66% only. The discount is always on the number of items sold, not on the number of items purchased.
- In case of successive discounts we can treat the problem as the problem of successive percentage change and can use the formula
Net discount =
Markup Price
- It is also known as list price or Tag price which is written on the item. The markup price written is always greater than the actual C.P of the item and the percentage rise in the markup price is on the C.P of the item.
- Percentage increase in the Markup price =
Example 1: The price of a trouser is marked 50% more than its cost price and a discount of 25% is offered on the marked price of the trouser by the shopkeeper. Find the percentage of profit/loss.
Sol. M.P = 1.5 C.P
S.P = 0.75 × 1.5 C.P = 1.125 C.P
So profit percentage = 12.5 %.
Example 2: After allowing a discount of 11.11%, a trader still makes a profit of 14.28%. At how much percent above the cost price does he mark on his goods?
Sol. Discount of 11.11% means a discount of
and 14.28% means
So selling price =C.P. =
M.P
So M.P =
C.P. So it is
× 100 = 28.56% more than the C.P.
Two different articles sold at the same selling price
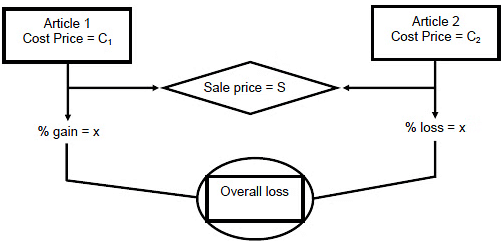
where x is the percent profit or loss on the transaction.
Example 1: Each of the two horses is sold for Rs. 1875. The first one is sold at 25% profit and the other one at 25% loss. What is the % loss or gain in this deal?
Sol. It is loss of
= 6.25 % loss.
Example 2: What is the total loss or gain (in rupees) in the above example?
Sol. Since he got 6.25 % loss means
loss.
So, his selling price should beof the C.P
So loss is
of the S.P =
= Rs. 250.
Faulty Balance
- Sometimes traders may sell their products at the rate at which they purchased them or even less than the actual cost incurred by them. Even in this transaction, they make a profit by cheating on volume. If the weighing balance of a shopkeeper reads 1000 grams for every 900 grams, what is the profit or loss the shopkeeper is making?
- On the other hand if the faulty balance reads 900 grams for every 1000 grams, is he still making profit? If not why?
Example 1: Instead of a meter scale, a cloth merchant uses a 120 cm scale while buying, but uses an 80 cm scale while selling the same cloth. If he offers a discount of 20% on the cash payment, what is his overall profit percentage?
Sol. When the merchant is buying he is using a scale of 120 cm instead of 100 cm thus multiplying factor
for him in this transaction =
When selling the cloth the merchant is measuring 80 cm for every 100 cm , so multiplying factor of this
transaction is =
For the discount offered by the merchant the multiplying factor =
Net profit =Hence making a profit of 20% in the whole transaction.
Example 2: Mr. A purchased an article and sold it to Mr. B at 20% profit. Mr. B sold it to Mr. C at 20% profit. If Mr. C paid Rs. 2880 to Mr. B, what is the profit in rupees earned by Mr. A ?
Sol. Assume that Mr. A purchased the article for Rs. X,
Then he sold it to Mr. B for Rs. 1.2X and Mr. B sold it to Mr. C for Rs. 1.2 × 1.2X = 1.44X.
This is given as Rs. 2880. So X = Rs. 2000.
Profit earned by A is 20% of X = Rs. 400.
Example 3: A cloth merchant allows 25% discount on a saree and still makes 20% profit. By selling a saree, he gained Rs. 160. What is the marked price of that saree?
Sol. He makes a profit of 20% and it is given as Rs. 160.
20% of C.P = 160
So C.P = Rs. 800.
So S.P = 800 + 160 = Rs. 960.
And 0.75 M.P = 960 (since he is giving 25% discount)
M.P = Rs. 1280
Example 4: A man purchased some chocolates at 80 per Rs 100 and same number of chocolates of other type at 120 per Rs. 100. He sold each chocolate per 1 rupee each, what is his profit/loss
percentage?
Sol.The first type of chocolate costs Rs. 100/80 rupees = 5/4 rupee.
The second type costs Rs. 100/120 = 5/6 rupee
Since he purchased both the chocolates in equal number, the
Average cost per chocolate is
But he is selling each chocolate at Re. 1. So he get a loss of
|
1335 videos|1432 docs|834 tests
|
FAQs on Profit & Loss - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year
| 1. What is the difference between discount and markup? |  |
| 2. How do you calculate the selling price after applying a discount? |  |
| 3. What is the formula to calculate profit or loss? |  |
| 4. How do faulty balances affect profit and loss calculations? |  |
| 5. What is the significance of understanding markup price in business? |  |





















