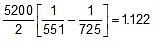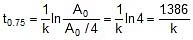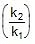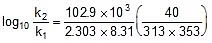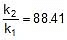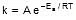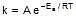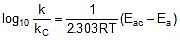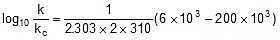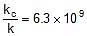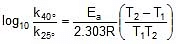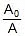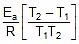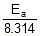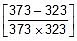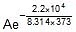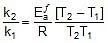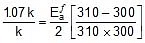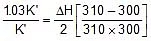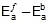Arrhenius Equation, Collision Theory & Pseudo First Order Reaction | Chemistry Class 12 - NEET PDF Download
What is the Arrhenius Equation?
The Arrhenius equation is an expression that provides a relationship between the rate constant (of a chemical reaction), the absolute temperature, and the A factor (also known as the pre-exponential factor; can be visualized as the frequency of correctly oriented collisions between reactant particles). It provides insight into the dependence of reaction rates on absolute temperature.
The expression of the Arrhenius equation is:
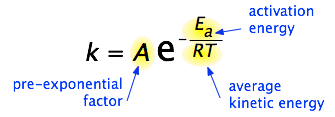
- k denotes the rate constant of the reaction
- A denotes the pre-exponential factor which, in terms of the collision theory, is the frequency of correctly oriented collisions between the reacting species
- e is the base of the natural logarithm (Euler’s number)
- Ea denotes the activation energy of the chemical reaction (in terms of energy per mole)
- R denotes the universal gas constant
- T denotes the absolute temperature associated with the reaction (in Kelvin)
If the activation energy is expressed in terms of energy per reactant molecule, the universal gas constant must be replaced with the Boltzmann constant (kB) in the Arrhenius equation.
Activation Energy (Ea)
Activation energy is the minimum amount of energy required for a chemical reaction to occur. It is the energy barrier that must be overcome for reactants to be transformed into products. The concept of activation energy is crucial in understanding how and why chemical reactions happen and what factors can affect the rate of these reactions.
- A mixture of magnesium and oxygen does not react at room temperature. But if a burning splinter is introduced to the mixture, it burns vigorously.
- Similarly a mixture of methane and oxygen does not react at room temperature, but if a burning match-stick is put in the mixture, it burns rapidly. Why it happen like this, that some external agents has to be introduced in order to initiate the reaction ?
- According to the theory of reaction rates "for a chemical reaction to take place, reactant molecules must make collisions among themselves". Now in actuality, only a fraction of collisions are responsible for the formation of products, i.e., not all collisions are effective enough to give products. So the collisions among reactant molecules are divided into two categories:-
Effective collisions and In-effective collisions
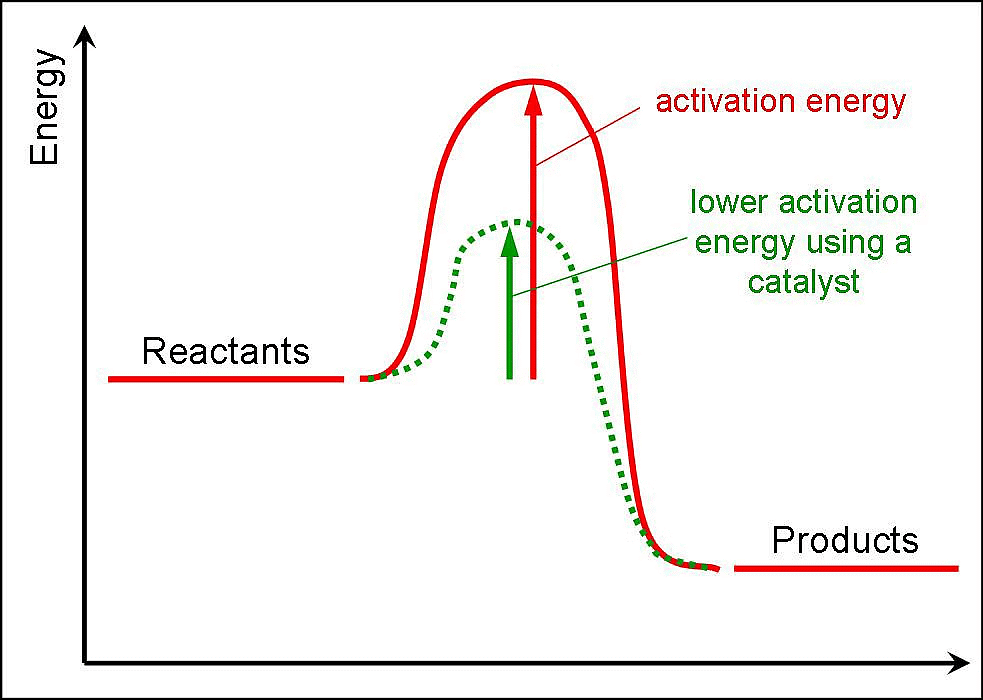
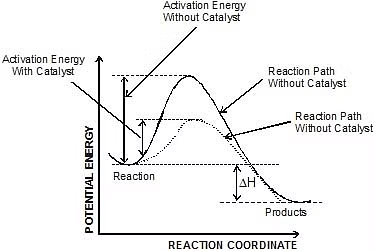
Effective collisions are collisions between the molecules that have energies equal to or above a certain minimum value. This minimum energy which must be possessed by the molecules in order to make an effective collision (i.e., to give a molecule of products) is called as threshold energy. So it is the effective collisions that bring about the occurrence of a chemical reaction.
Ineffective collisions are the collisions between the molecules which does not posses the threshold energy. These can not result in a chemical reaction.
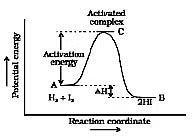
Now most of the times, the molecules of reactants do not possess the threshold energy. So in order to make effective collisions (i.e., to bring about the chemical reaction), an additional energy is needed to be absorbed by the reactant molecules. This additional energy which is absorbed by the molecules so that they achieve the threshold energy is called as energy of activation or simply activation energy. It is represented as Ea.
A reaction which needs higher activation energy is slow at a given temperature.
Activation Energy Curve in Exothermic Reaction
For example : is faster at ordinary temperature whereas the following reaction :
CO(g) + → CO2(g) is slower at the same temperature as the value of Ea for the second reaction is much higher.
Variation in Arrhenius equation
Type -1 :
log k = 2 - ; A = ? Ea = ?
k = Ae-Ea/RT
loge k = loge A -
log k = log A -
log10 A = 2 A = 102 = 100
Ea = 2.303 x R x 5 x 10-3
Type -2 : Temperature Variation :
r1 K1
T1
r2 K2
T2
log k1 = log A - , log k2 = log A -
Type -3 : Addition of Catalyst :
r1 k1
no catalyst
Ea
T
r2 k1
catalyst
Eac
T
log k1 = log A -
log k2 = log A -
log
Type -4 : Both Catalyst and Temperature :
Q. At 278 oC the half life period for the first order thermal decomposition of ethylene oxide is 363 min and the energy of activation of the reaction is 52,00 cal/mole. From these data estimate the time required for ethylene oxide to be 75% decomposed at 450�C.
Sol. ln
=
=
t1/2 (at 450oC) = 118.24 min.
Now
Therefore, t0.75 =
x 118.24 = 236.48 min
Example. The activation energy of the reaction : A + B → products is 102.9 kJ/mol. At 40oC, the products are formed at the rate of 0.133 mol/L/min. What will be rate of formation of products at 80oC?
Sol. Let the rate law be defined as
At T1 : r1 = k1[A]x[B]y
At T2 : r2 = k2[A]x [B]y
⇒ r2 = r1
Using Arrhenius equation find k at 40oC.
log10
=
⇒
⇒ log10
= 1.95 ⇒
⇒ r2 = 0.133 x 88.41 = 11.76 mol/L/min
Q. The activation energy of a non-catalysed reaction at 37oC is 200 kcal/mol and the activation energy of the same reaction when catalysed decreases to only 6.0 kcal/mol. Calculate the ratio of rate constants of the two reactions.
Sol. We know that :
Let k = rate constant for non-catalysed reaction and kc rate constant for catalysed reaction. Let Ea be the activation energy for non-catalysed reaction and Eac be the energy of activation of catalysed reaction.
1.
2.
⇒
⇒
⇒
⇒
⇒
or
Q. A first order reaction A → B requires activation energy of 70 kJ/mol. When 20% solution of A was kept at 25oC for 20 minutes, 25% decomposition took place. What will be the percent decomposition in the same time in a 30% solution maintained at 40oC? Assume that the activation energy remains constant in this range of temperature.
Sol. Note : It does not matter whether you take 20%, 30%, 40% or 70% of A.
At 25oC, 20% of A decomposes 25%
⇒ kt = 2.303 log10
⇒ k(40) = 2.303 log10
⇒ k(at 25oC) = 0.0143 min-1
Using Arrhenius equation find k at 40oC.
⇒ k(at 40oC) = 0.055 min-1
Now calculate % decomposition at 40oC using first order kinetics.
kt = 2.303 log10
⇒ 0.055 x 40 = 2.303 log10(
)
⇒ x = 67.1 ≡ 67.1% decomposition of A at 40oC.
Q. The rate constant of a reaction is 1.5 x 107 sec-1 at 50oC and 4.5 x 107 sec-1 at 100oC. Evaluate the Arrhenius parameters A and Ea.
Sol. Therefore, 2.303 log10
=
Therefore, 2.303 log10
=
Therefore, Ea = 2.2 x 104 J mol-1
Now,
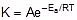
Therefore, 4.5 x 107 =Therefore, A = 5.42 x 1010
Q. The rate constant of a reaction increases by 7% when its temperature is raised from 300 K to 310 K, while its equilibrium constant increases by 3%. Calculate the activation energy of the forward and reverse reactions.
Sol. Rate constant at 300K = k
Therefore, Rate constant at 310 K = k +
= 1.07 k
Thus, 2.303 log
2.303 log
Therefore,
= 1258.68 cal
Now, equilibrium constant at 300 K = K'
Equilibrium constant at 310 K = K' + 3/100 x K' = 1.03 K'
Using 2.303 log
=
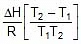
2.303 log
Therefore, ΔH = 549.89 cal
Since, ΔH =
Therefore, 549.89 = 1258.68 -
Therefore,
= 708.79 cal
Q. At 380oC, the half life period for the first order decomposition of H2O2 is 360 min. The energy of activation of the reaction is 200 kJ mol-1. Calculate the time required for 75% decomposition at 450oC. [IIT 1995]
Sol. K1 = 0.693/360 min-1 at 653 K and
Ea = 200 x 103 J, K2 = ? at 723 K, R = 8.314 J
Therefore, From 2.303 log10 (K2 / K1) = (Ea/R)[(T2 - T1)/(T1T2)]
K2 = 0.068 min-1
Now, t =
log10
= 20.39 minute
Factors Affecting Rate of Reaction
Several factors affect the rate of a chemical reaction. These factors influence how quickly reactants are converted into products. Here are the main factors:
(a) Catalyst
The rate of reaction increased by addition of catalyst, because catalyst lowers, the activation energy and increased the rate of reaction. A catalyst is a substance which increases the rate of a reaction without itself undergoing any permanent chemical change. For example, MnO2 catalyses the following reaction so as to increase its rate considerably.
| 2KClO3 |
The word catalyst should not be used when the added substance reduces the rate of reaction. The substance is then called inhibitor. The action of the catalyst can be explained by intermediate complex theory. According to this theory, a catalyst participates in a chemical reaction by forming temporary bonds with the reactants resulting in an intermediate complex. This has a transitory existence and decomposes to yield products and the catalyst.
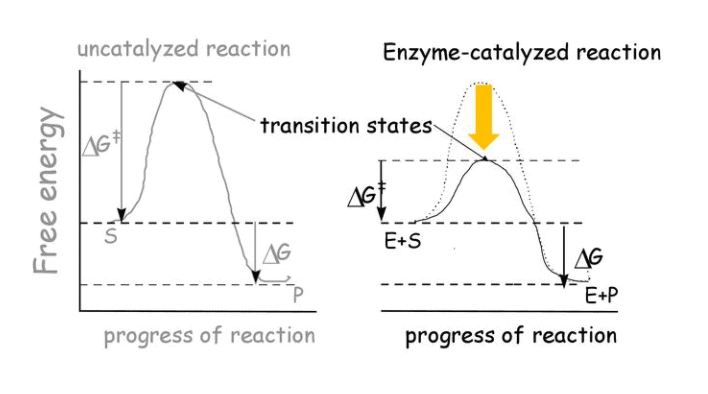
- A catalyst is believed to provide an alternative pathway or reaction mechanism by reducing the activation energy between reactants and products, thereby lowering the potential energy barrier, as illustrated in the figure.
- According to the Arrhenius equation, a lower activation energy results in a faster reaction rate. A small quantity of catalyst can catalyze a large amount of reactants. Importantly, a catalyst does not alter the Gibbs energy (ΔG) of a reaction. It can catalyze spontaneous reactions but cannot make non-spontaneous reactions proceed.
- Additionally, a catalyst does not change the equilibrium constant of a reaction; instead, it helps the system reach equilibrium more quickly. It accelerates both the forward and backward reactions to the same extent, so the equilibrium state remains unchanged but is achieved sooner.
(b) Temperature
With increase in temperature the rate of reaction increases. It is generally found for every 10o increase in temperature. The rate constant double.
Raising the temperature increases the kinetic energy of the molecules, leading to more frequent and energetic collisions. This typically results in a faster reaction rate. According to the Arrhenius equation, an increase in temperature decreases the activation energy, thus increasing the rate constant.
The ratio of rate constants with 10o difference in their temperature is called the temperature coefficient.
= Q = Temperature coefficient of reaction
2
 (c) Concentration
(c) Concentration
Rate = A e-Ea/RT [A]m [B]n - - - - - - - - -
With increase in concentration of reactants the rate of the reaction increases because number of, collision (effective collisions) increases.
Increasing the concentration of reactants generally increases the rate of reaction. This is because more reactant molecules are present, leading to a higher probability of collisions and, thus, reactions.
(d) Nature of Reactants
Different substances react at different rates depending on their chemical nature. For instance, ionic compounds in aqueous solutions tend to react more quickly than covalent compounds because the ions can move freely and interact more readily.
- Ionic Reactants : Generally ionic reactions in aq. media are fast than the reaction involving covalent reactants.
- Covalent Reactants : As covalent reactants involving breaking of bond then formation of bond where as ionic reaction involve in single step.
(e) Surface Area
For reactions involving solids, increasing the surface area (e.g., by crushing a solid into a powder) exposes more reactant particles to the other reactant, increasing the reaction rate. Increase in surface area increases the number of collisions and hence rate increases.
 Increasing Surface Area increases the Rate of Reaction
Increasing Surface Area increases the Rate of Reaction
(f) Radiation
Some reactions exposes to sunlight also increases the rate of reactionEffect of temperature on Rate of Reaction
Temperature is one of the parameters that can affect the rate of a chemical reaction considerably. We have often seen milk boiling on a gas stove. The rate at which a specific quantity of milk boils depends on the flame of the stove. If the flame height is maximum, the milk boils in less time and if the flame height is minimum, the milk takes more time to boil. Here the flame height resembles temperature.

Pseudo First Order Reaction
The order of a reaction is sometimes altered by conditions. Consider a chemical reaction between two substances when one reactant is present in large excess. During the hydrolysis of 0.01 mol of ethyl acetate with 10 mol of water, amounts of the various constituents at the beginning (t = 0) and completion (t) of the reaction are given as under.
The concentration of water does not get altered much during the course of the reaction. So, in the rate equation Rate = k'[CH3COOC2H5] [H2O] the term [H2O] can be taken as constant. he equation, thus, becomes Rate = k[CH3COOC2H5] where k = k'[H2O] and the reaction behaves as first order reaction. The molecularity of acidic hydrolysis of sucrose and esters is 2, whereas their order is 1. In both the reactions water is in excess so that its concentration remains constant throughout the reaction. The rate of reaction therefore depends only on the concentration of sucrose and ester in two reactions respectively. So the reactions in which the molecularity is 2 or 3 but they conform to the first order kinetics are known as pseudo first order reactions OR pseudo uni-molecular reactions.
C12H22O11 + H2O + H+ → C6H12O6(glucose) + C6H12O6(fructose)
CH3COOC2H5(ester) + H2O + H+ → CH3COOH + C2H5OH
(In both the reactions, H ion acts as a catalyst)
nth Order kinetics
A product
⇒ -
⇒
⇒
⇒
⇒
Half-life (t1/2) for n order reaction
at t = t1/2 , [A]t =
⇒ k =
⇒ t 1/2 = ⇒
Q. For the non-equilibrium process, A + B → Products, the rate is first order w.r.t A and second order w.r.t. B. If 1.0 mole each of A and B are introduced into a 1 litre vessel and the initial rate were 1.0 x 10-2 mol/litre-sec, calculate the rate when half of the reactants have been used.
Sol. Rate = K[A] [B]2
Therefore, 10-2 = K[1] [1]2
or K = 10-2 litre2 mol-2 sec-1
Now ratell = 10-2 x 0.5 x (0.5)2
or New rate = 1.2 x 10-3 mol/L-sec
Analysis of some important first-order reactions
(i) Decomposition of Hydrogen peroxide (H2O2)
H2O2(g) → H2O(g) + 1/2O2(g)
The rate of this first order reaction is measured by titrating a fixed volume of H2O2 (undecomposed) against a standard solution of KMnO4. Here KMnO4 acts as oxidising agent and H2O2 as reducing agent. The volumes of KMnO4 used for H2O2 after regular intervals of time are as follows.
Time instants | t = 0 | t1 | t2 | t3 | t4 | t5 |
Vol. of KMnO4 | Vo | V1 | V2 | V3 | V4 | V5 |
Volume of KMnO4 at t = 0 corresponds to volume of H2O2 initially present.
⇒ A0 ∝ V0
Volume of KMnO4 at time instants t1, t2, t3, .................... corresponds to volume of H2O2 remaining after t1, t2, t3, .................
⇒ A ∝ Vt
Now it being a first order reaction, follows first order kinetics, so
k t = 2.303 log10
Now using the above expression, if we calculate the values of k for different time intervals t1, t2, ........... (for actual numerical data), the values of k should be same if the reaction follows first order kinetics.
(ii) Decomposition of ammonium nitrite (NH4NO2) and benzene diazonium chloride (C6H5N = NCl)
NH4NO2(g) → 2 H2O(g) + N2(g)
C6H5 - N = N - Cl(g) → C6H5 - Cl(g) + N2(g)
The rate of both the reaction is studied (measured) in similar manner. The volume of nitrogen (N2) is collected after a regular interval of time as follows
Time instants | t = 0 | ti | t2 | t3 | t4 | t |
Vol. of N2 | 0 | V1 | V2 | V3 | V4 | V∝ |
At t = 0, clearly the volume of N2 = 0
Time instant t = ∞ means the end of a reaction i.e., when whole of NH4NO2 or C6H5 - N = N - Cl is decomposed.
⇒ At t = ∞, V∞ corresponds to the initial volume of NH4NO2 or C6H5 - N = N - Cl
(Note that the ratio of stoichiometric coefficient for both N2 : NH4NO2 or N2 : C6H5N = NCl is 1 : 1)
⇒ A0 ∝ V∞
At t = t1, t2, t3................ the volume of N2 corresponds to concentration of product formed i.e., equal to x.
⇒ x ∝ Vt
⇒ A0 - x ∝ V∞ - Vt
⇒ kt = 2.303 log10
(iii) Hydrolysis of Esters (CH3COOC2H5 )
CH3COOC2H5 (ester) + H2O + HCl(H+ ) → CH3COOH + C2H5OH
The reaction rate is measured by titrating the acid (CH3COOH) produced against a standard alkali solution. Note that when a test sample is prepared from the reacting mixture, there are two acids : one is mineral acid H (HCl or any other) and second is CH3COOH produced. So volume of alkali used gives titration value for both acids. The data is collected in the following manner.
Time instants | t = 0 | t1 | t2 | t3 | t4 | t∝ |
Vol. of NaOH | Vo | V1 | V2 | V3 | V4 | V∝ |
At t = 0, V0 is the volume NaOH used to neutralise the mineral acid present (H ) being used as catalyst.
(At t = 0, no CH3COOH is yet produced)
At t = ∞ (i.e., at the end of hydrolysis), V∞, is the volume of NaOH used to neutralise whole of CH3COOH plus vol. of HCl present At t = ∞, volume of CH3COOH corresponds to volume of ester taken initially
⇒ A0 ∝ V∞ - V0 (as V0 = vol. of HCl)
At t = t1, t2, t3............ V1, V2, V3, ................corresponds to vol. of HCl plus vol. of CH3COOH being produced.
⇒ x ∝ Vt - V0
⇒ A0 - x ∝ (V∞ - V0) - (Vt - V0)
⇒ A0 - x ∝ V∞ - Vt
 ⇒ kt = 2.303 log10
⇒ kt = 2.303 log10
(iv) Inversion of Cane Sugar (C12H22O11)
C12H22O11 + H2O + H+ → C6H12O6(glucose) + C6H12O6 (fructose)
The rate is measured by measuring the change in the angle of rotation (optical activity) by a polarimeter. Sucrose is dextro-rotatory, glucose is dextro-rotatory and fructose is leavo-rotatory. The change produced in rotatory power in time t gives a measure of x, the quantity of sucrose decomposed in that time. The total change in the rotatory power produced at the end of the reaction gives the measure of A0, the initial concentration of sucrose.
If r0, r1 and r∞ represent rotations at the start of reaction, after time t and at the end of reaction respectively,
then
⇒ A0 ∝ r0 - r∞ and x ∝ r0 - rt
(v) Decomposition of AsH3(g)
In first-order reactions involving gases, sometime measuring the pressure of the reaction mixture is very good method for measuring reaction rates.
For example consider decomposition of arsine gas (AsH3)
AsH3(g) → As(s) +
The rate of reaction is measured as the increase in pressure of the reaction mixture. Note that there is an increase in number of moles of the gaseous products to the right, so as the reaction proceeds, there will be an increase in pressure of contents (P ∝ n).
Let the initial pressure of AsH3(g) is P0, if x is the decrease in pressure of AsH3(g) after time t.
Arsenic is solid, so P(AS) = 0
After time t, let Pt be the total pressure, then
Pt = P(AsH3) + P(H2) = (P0 - x) +
⇒ Pt = P0 + ⇒ x = 2(Pt - P0)
Now A0 ∝ P0
and A ∝ P0 - x ≡ P0 - 2 (Pt - P0) ≡ 3P0 - 2Pt
⇒ kt = 2.303 log10
On similar pattern, please try to write the expression for Ist order rate law for following first-order reactions. (in terms of P0 and Pt)
1. N2O(g) → N2(g) + O2(g)
2. (CH3)3C - O - O - C(CH3)(g) → 2(CH3)2C = O(g) + C2H6(g)
Complex (First order) kinetics
(A) Parallel Kinetics
Rate of change of A = [rate of change of A]I + [rate of change of A]II
- = K1 [A] + K2 [A],
,
⇒
% of B in the mix of A & B =
% of C in the =
Generalization
,
Q. An organic compound A decomposes following two parallel first order mechanisms :
;
and k1 = 1.3 x 10-5 sec-1.
Calculate the concentration ratio of C to A, if an experiment is allowed to start with only A for one hour.
Sol.
But k1 = 1.3 x 10-5 sec-1 ; k2 = 9 x 1.3 x 10-5 sec-1 = 117 x 10-5 sec-1
(k1 + k2) = (1.3 x 10-5) + (11.7 x 10-5) sec-1 = 13 x 10-5 sec-1 ....(1)
Also ⇒ [B]t =
...(2)
⇒ ;
= (k1 + k2)t
⇒ [from eq. (2)] ⇒
⇒ = 13 x 10-5 x 60x 60 = 0.468 [from eq. (1)]
⇒ 1 + = 1.5968 ;
Series Kinetics
Series Kinetics
,
,
,
Graph of [A], [B], [C] Vs t:
Time when [B] is maximum
[B] =
t =
Reversible Kinetics
O < t < teq Chemical kinetics, teq
t <
Chemical Equilibrium
At equilibrium, rf = rb , k1 [A] equilibrium = k2 [B] equilibrium ,
- 1,
............ (I)
= - k1 [A] + k2 [B],
= - k1 [A] + k2 [ [A]o - [A] ] = - (k1 + k2) [A] + k2 [A]o
= (k1 + k2)
By substituting the value from equation (I)
⇒
Q. For a reversible first order reaction,
A B ; Kf = 10-2 sec-1
and = 4 ; If A0 = 0.01 ML-1 and B0 = 0, what will be concentration of B after 30 sec ?
Sol.
=
=
Therefore, Kb = 0.25 x 10-2 and xeq =
= 0.008
t =
30 =
log
Therefore,
Therefore, x = 2.50 x 10-3
Ways to determine Order of Reaction
(1) Initial Rate Method
A + B product
rate = k [A]m [B]n ; Order = m + n
| [A] | [B] | rate |
Experiment 1 | 0.1 | 0.1 | 2 x 10-3 |
Experiment 2 | 0.1 | 0.2 | 4 x 10-3 |
Experiment 3 | 0.2 | 0.1 | 32 x 10-3 |
Experiment (1) and Experiment (2)
n = 1
Experiment (1) and Experiment (3)
m = 4
Order (m + n) = 4 + 1 = 5
(2) Half - life method
t1/2 ∝
2 hr 0.2
n = 0
(3) Integrated Rate law Method
A product
t = 0 1000 M
t = 60 sec 100 M
t = 120 sec 10 M
n = 0 k = =
= 15
k =
n = 1
k =
k =
(4) Ostwald Isolation method
rate = k[A]m [B]n [C]o [D]p - - - - - - - -
Experiment 1 : [A] = In small quantity ; [B], [C], [D] - - - - - - - in excess
The rate equation reduces to
rate = k' [A]m r1 = k' [A]1m
r2 = k' [A]2m
, log
Experiment 2: [B] = In small quantity . & [A], [C], [D] - - - - - - in excess.
rate = k' [B]n repeated
Order of reaction = m + n + o + p + - - - - - - - -
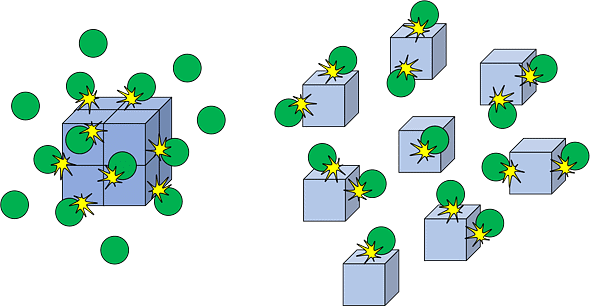
Collision Theory of Chemical Reaction
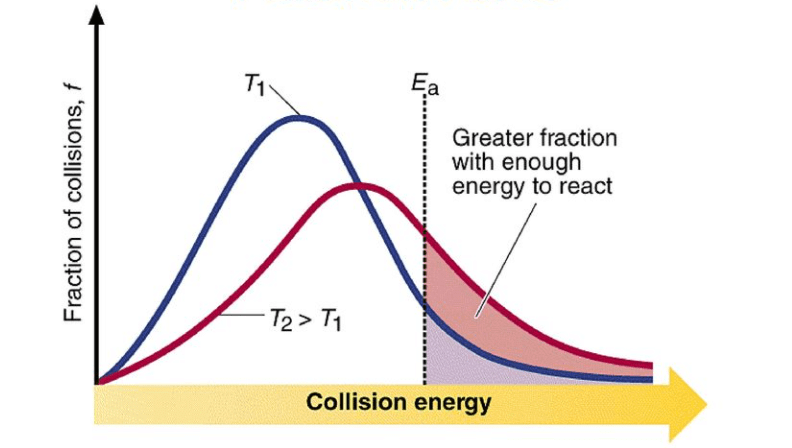
- Though the Arrhenius equation is applicable under a wide range of circumstances, collision theory, which was developed by Max Trautz and William Lewis in 1916 -18, provides greater insight into the energetic and mechanistic aspects of reactions. It is based on the kinetic theory of gases.
- According to this theory, the reactant molecules are assumed to be hard spheres and reaction is postulated to occur when molecules collide with each other.
- The number of collisions per second per unit volume of the reaction mixture is known as collision frequency (Z). Another factor that affects the rate of chemical reactions is activation energy (as we have already studied). For a bimolecular elementary reaction.
A + B → Products rate of reaction can be expressed as
Rate =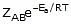 ..............(1)
..............(1)
where 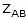 represents the collision frequency of reactants, A and B and
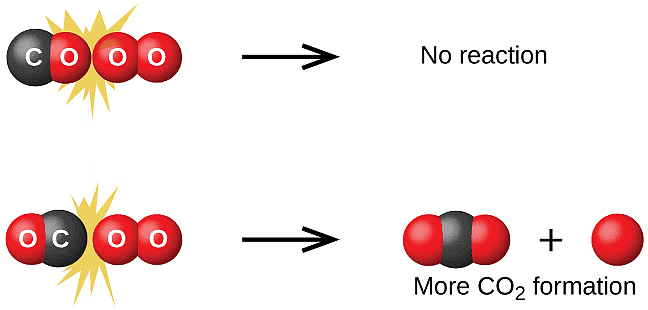
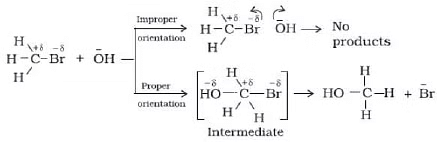
represents the collision frequency of reactants, A and B and 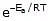 represents the fraction of molecules with energies equal to or greater than Ea. Comparing (1) with Arrhenius equation, we can say that A is related to collision frequency. Equation (1) predicts the value of rate constants fairly accurately for the reactions that involve atomic species or simple molecules but for complex molecules significant deviations are observed. The reason could be that all collisions do not lead to the formation of products. The collisions in which molecules collide with sufficient kinetic energy (called threshold energy*) and proper orientation, so as to facilitate breaking of bonds between reacting species and formation of new bonds to form products are called as effective collisions.
represents the fraction of molecules with energies equal to or greater than Ea. Comparing (1) with Arrhenius equation, we can say that A is related to collision frequency. Equation (1) predicts the value of rate constants fairly accurately for the reactions that involve atomic species or simple molecules but for complex molecules significant deviations are observed. The reason could be that all collisions do not lead to the formation of products. The collisions in which molecules collide with sufficient kinetic energy (called threshold energy*) and proper orientation, so as to facilitate breaking of bonds between reacting species and formation of new bonds to form products are called as effective collisions.
To account for effective collisions, another factor P, called the probability or steric factor is introduced. It takes into account the fact that in a collision, molecules must be properly oriented i.e.,
Rate = 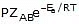
Thus, in collision theory activation energy and proper orientation of the molecules together determine the criteria for an effective collision and hence the rate of a chemical reaction.
Mechanism of Reaction
Reactions can be divided into
Elementary/Simple/single step
Complex/multi-step
Elementary Reaction
These reaction take place in single step without formation of any intermediate
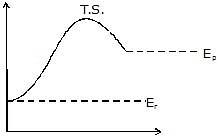
For elementary reaction we can define molecularity of the reaction which is equal to no of molecules which make transition state or activated complex because of collisions in proper orientation and with sufficient energy
molecularity will always be a natural no
1 = unimolecular one molecular gets excited (like radioactivity)
2 = bimolecular
3 = trimolecular
Molecularity < 3 because the probability of simultaneous collision between 4 or mor molecules in proper orientation is very low
For elementary reaction there is only single step and hence it is going to be rate determining step so order of an elementary reaction is its molecularity
Order of elementary reaction w.r.t reactant = stoichiometric co-efficient of the reactant
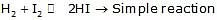
rate = k [H2] [I2]
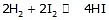 (no elementary)
(no elementary)
reaction obtained by multiplying and elementary reaction with some no will not be of elementary nature
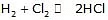
order = 0
Complex Reaction
Reaction which proceed in more than two steps or having some mechanism. (sequence of elementary reaction in which any complex reaction proceeds)
For complex reaction each step of mechanism will be having its own molecularity but molecularity of net complex reaction will not be defined.
Order of complex reaction can be zero fractions whole no, even negative w.r.t some species.
Order of reaction or rate law of reaction is calculated with the help of mechanism of the reaction generally using rate determine step (R.D.S) if given.
Rate law of a reaction is always written in terms of conc. of reactant, products or catalysts but never in terms of conc. of intermediates.
The mechanism of any complex reaction is always written in terms of elementary steps, so molecularity of each of these steps will be defined but net molecularity of complex reaction has no meaning.
The mechanism of most of the reaction will be calculated or predicted by using mainly the following approximation.
The Rate-Determining-Step Approximation %
In the rate-determining-step approximation (also called the rate-limiting-step approximation or the equilibrium approximation), the reaction mechanism is assumed to consist of one or more reversible reactions step, which in turn is followed by one or more rapid reactions. In special cases, there may be no equilibrium steps before the rate-determining step or no rapid reactions after the rate-determining step.
When steps 2 B 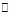 (C) is assumed to be the rate-determining step. For this assumption to be valid, we must have k-1 >> k2. The slow of
(C) is assumed to be the rate-determining step. For this assumption to be valid, we must have k-1 >> k2. The slow of 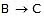 compared with
compared with 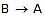 ensures that most B molecules go back to A rather than going to C, thereby ensuring that step
ensures that most B molecules go back to A rather than going to C, thereby ensuring that step 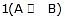 remains close to equilibrium. Further-more, we must have k3 >> k2 and k3 >> k-2 to ensure that step 2 acts as a"bottleneck" and that product D is rapidly formed from C. The overall rate is then controlled by the rate-determining step
remains close to equilibrium. Further-more, we must have k3 >> k2 and k3 >> k-2 to ensure that step 2 acts as a"bottleneck" and that product D is rapidly formed from C. The overall rate is then controlled by the rate-determining step 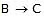 . (Note that since k3 >> k-2, the rate-limiting step is not in equilibrium.) Since we are examining the rate of the forward reaction
. (Note that since k3 >> k-2, the rate-limiting step is not in equilibrium.) Since we are examining the rate of the forward reaction 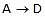 , we further assume that k2[B] >> k-2[C]. During the early stage of the reaction, the concentration of C will be low compared with B, and this condition will hold. Thus we neglect the reverse reaction for step 2. Since the rate-controlling step is taken to be essentially irreversible, it is irrelevant whether the rapid steps after the rate-limiting step are reversible or not. The observed rate law will, depends only on the nature of the equilibrium that precede the rate-determining step and on this step itself.
, we further assume that k2[B] >> k-2[C]. During the early stage of the reaction, the concentration of C will be low compared with B, and this condition will hold. Thus we neglect the reverse reaction for step 2. Since the rate-controlling step is taken to be essentially irreversible, it is irrelevant whether the rapid steps after the rate-limiting step are reversible or not. The observed rate law will, depends only on the nature of the equilibrium that precede the rate-determining step and on this step itself.
Arrhenius Equation
Number of effective collisions = Number of collision x fraction.
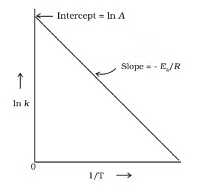
F k = A e-Ea/RT
Where , k = rate constant of reaction
A = Pre exponential factor or Arrhenius constant or Frequency factor.
Ea = Activation energy
R = Universal gas constant
T = Absolute temperature.
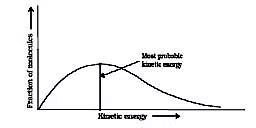
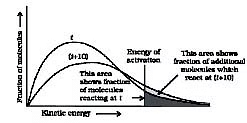
⇒ Fraction of molecules undergoing effective collision 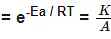
Variation in Arrhenius equation
Type -1 :
log k = 2 - 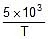 ; A = ? Ea = ?
; A = ? Ea = ?
k = Ae-Ea/RT
loge k = loge A - 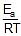
log k = log A - 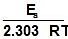
log10 A = 2 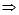 A = 102 = 100
A = 102 = 100
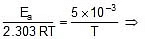 Ea = 2.303 x R x 5 x 10-3
Ea = 2.303 x R x 5 x 10-3
Type -2 : Temperature Variation :
r1 K1
K1 T1
T1
r2 K2
K2 T2
T2
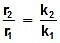
log k1 = log A - 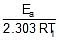 , log k2 = log A -
, log k2 = log A - 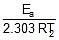
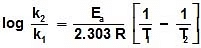
Type -3 : Addition of Catalyst :
r1 k1
k1 no catalyst
no catalyst Ea
Ea T
T
r2 k1
k1 catalyst
catalyst Eac
Eac T
T
log k1 = log A - 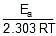
log k2 = log A - 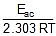
log 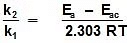
Type -4 : Both Catalyst and Temperature :
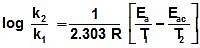
Q. At 278 oC the half life period for the first order thermal decomposition of ethylene oxide is 363 min and the energy of activation of the reaction is 52,00 cal/mole. From these data estimate the time required for ethylene oxide to be 75% decomposed at 450�C.
Sol. ln =
= 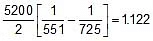
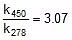 =
= 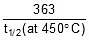 t1/2 (at 450oC) = 118.24 min.
t1/2 (at 450oC) = 118.24 min.
Now 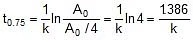
Therefore, t0.75 =  x 118.24 = 236.48 min
x 118.24 = 236.48 min
Q. The activation energy of the reaction : A + B → products is 102.9 kJ/mol. At 40oC, the products are formed at the rate of 0.133 mol/L/min. What will be rate of formation of products at 80oC?
Sol. Let the rate law be defined as
At T1 : r1 = k1[A]x[B]y
At T2 : r2 = k2[A]x [B]y
⇒ r2 = r1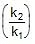
Using Arrhenius equation find k at 40oC.
log10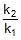 =
= 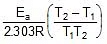 ⇒
⇒ 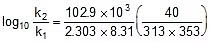
⇒ log10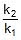 = 1.95 ⇒
= 1.95 ⇒ 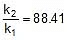
⇒ r2 = 0.133 x 88.41 = 11.76 mol/L/min
Q. The activation energy of a non-catalysed reaction at 37oC is 200 kcal/mol and the activation energy of the same reaction when catalysed decreases to only 6.0 kcal/mol. Calculate the ratio of rate constants of the two reactions.
Sol. We know that :
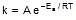
Let k = rate constant for non-catalysed reaction and kc rate constant for catalysed reaction. Let Ea be the activation energy for non-catalysed reaction and Eac be the energy of activation of catalysed reaction.
1. 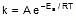
2. 
⇒ 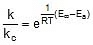 ⇒
⇒ 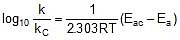
⇒ 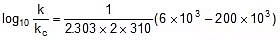
⇒ 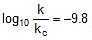 ⇒
⇒ 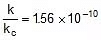 or
or 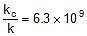
Q. A first order reaction A → B requires activation energy of 70 kJ/mol. When 20% solution of A was kept at 25oC for 20 minutes, 25% decomposition took place. What will be the percent decomposition in the same time in a 30% solution maintained at 40oC? Assume that the activation energy remains constant in this range of temperature.
Sol. Note : It does not matter whether you take 20%, 30%, 40% or 70% of A.
At 25oC, 20% of A decomposes 25%
⇒ kt = 2.303 log10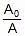
⇒ k(40) = 2.303 log10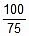 ⇒ k(at 25oC) = 0.0143 min-1
⇒ k(at 25oC) = 0.0143 min-1
Using Arrhenius equation find k at 40oC.
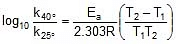
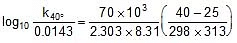 ⇒ k(at 40oC) = 0.055 min-1
⇒ k(at 40oC) = 0.055 min-1
Now calculate % decomposition at 40oC using first order kinetics.
kt = 2.303 log10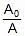
⇒ 0.055 x 40 = 2.303 log10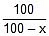
⇒ x = 67.1 ≡ 67.1% decomposition of A at 40oC.
Q. The rate constant of a reaction is 1.5 x 107 sec-1 at 50oC and 4.5 x 107 sec-1 at 100oC. Evaluate the Arrhenius parameters A and Ea.
Sol. Therefore, 2.303 log10 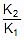 =
= 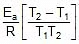
Therefore, 2.303 log10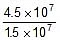 =
= 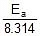
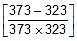
Therefore, Ea = 2.2 x 104 J mol-1
Now, 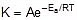 Therefore, 4.5 x 107 =
Therefore, 4.5 x 107 = 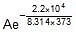
Therefore, A = 5.42 x 1010
Q. A reaction proceeds five times more at 60oC as it does at 30oC. Estimate energy of activation.
Sol. Given, T2 = 60 + 273 = 333 K, T1 = 30 + 273 = 303 K,
R = 1.987 x 10-3 kcal
r = k [ ]n (at a temperature T)
Therefore, 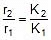 (at temp. T2 and T1)
(at temp. T2 and T1)
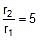 Therefore,
Therefore, 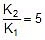
2.303 log10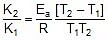
Therefore, 2.303 log10 5 = 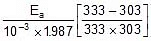
Ea = 10.757 kcal mol-1
Q. The rate constant of a reaction increases by 7% when its temperature is raised from 300 K to 310 K, while its equilibrium constant increases by 3%. Calculate the activation energy of the forward and reverse reactions.
Sol. Rate constant at 300K = k
Therefore, Rate constant at 310 K = k + 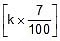 = 1.07 k
= 1.07 k
Thus, 2.303 log 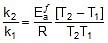
2.303 log 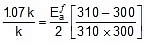
Therefore, 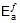 = 1258.68 cal
= 1258.68 cal
Now, equilibrium constant at 300 K = K'
Equilibrium constant at 310 K = K' + 3/100 x K' = 1.03 K'
Using 2.303 log 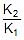 =
= 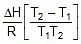
2.303 log 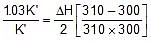
Therefore, ΔH = 549.89 cal
Since, ΔH = 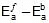
Therefore, 549.89 = 1258.68 - 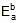
Therefore, 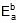 = 708.79 cal
= 708.79 cal
Q. At 380oC, the half life period for the first order decomposition of H2O2 is 360 min. The energy of activation of the reaction is 200 kJ mol-1. Calculate the time required for 75% decomposition at 450oC. [IIT 1995]
Sol. K1 = 0.693/360 min-1 at 653 K and
Ea = 200 x 103 J, K2 = ? at 723 K, R = 8.314 J
Therefore, From 2.303 log10 (K2 / K1) = (Ea/R)[(T2 - T1)/(T1T2)]
K2 = 0.068 min-1
Now, t = 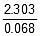 log10
log10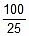 = 20.39 minute
= 20.39 minute
|
75 videos|278 docs|78 tests
|
FAQs on Arrhenius Equation, Collision Theory & Pseudo First Order Reaction - Chemistry Class 12 - NEET
| 1. What is the Arrhenius Equation and how is it related to the rate of reaction? |  |
| 2. How does temperature affect the rate of a chemical reaction according to the Arrhenius Equation? |  |
| 3. What is the Collision Theory of Chemical Reactions and how does it relate to the Arrhenius Equation? |  |
| 4. What is a Pseudo First Order Reaction and how does it differ from a first-order reaction? |  |
| 5. How can the order of a reaction be determined experimentally? |  |