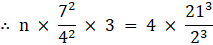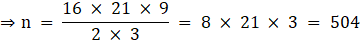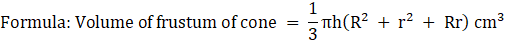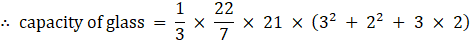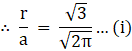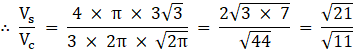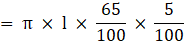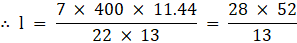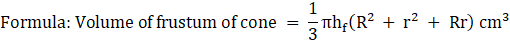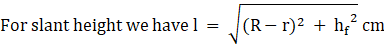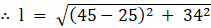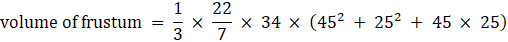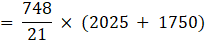RS Aggarwal Solutions: Volume and Surface Area of Solids- 6 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download

Q.1. Find the number of solid sphere, each of diameter 6 cm, that could be moulded to
Form a solid metallic cylinder of height 45 cm and diameter 4 cm.

Given: Diameter of each solid sphere = 6 cm
∴ Radius of each sphere = 6/2 = r_s = 3 cm
Diameter of cylinder = 4 cm
∴ Radius of cylinder = 4/2 = r_c = 2 cm
Height of cylinder = h = 45 cm
Formula: volume of sphere = (4/3) × π × r_s³
Volume of cylinder = π × r_c² × h
Spheres are moulded to form cylinder which means the volume remains the same
Let ‘n’ be the number of spheres required
i.e. volume of n spheres = volume of cylinder
∴ n × (4/3) × π × 3³ = π × 2² × 45
n × 4 × 27 = 4 × 3 × 45
n = 45/9 = 5
Number of solid spheres made = 5

Q.2. Two right circular cylinder of equal volume have their height in the ratio 1:2. What is the ratio of their radii?

Let the two cylinders be with volume V₁ and V₂ with their respective radii and height as r₁, r₂ and h₁, h₂
Now given ratio of their heights i.e. h₁:h₂ = 1:2
∴ h₁/h₂ = 1/2
Volume of cylinder = πr²h
Given that volumes of both cylinder are equal i.e. V₁ = V₂
∴ π × r₁² × h₁ = π × r₂² × h₂
h₁/h₂ = r₂²/ r₁²
r₂²/ r₁² = 1/2
r₂/r₁ = 1/√2
r₁/r₂ = √2/1
Therefore the ratio of their radii is r₁:r₂ = √2:1

Q.3. A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, find the total area of the canvas required.

Given: diameter of base of cone and the cylinder = 105 m
∴ Radius of cylinder = r_cl = 105/2 = 51 m
Radius of cone = r_co = 105/2 = 51 m
Height of cylinder = h = 4 m
Slant height of cone = l = 40 m
Formula: Surface area of cylinder = 2πr_clh + 2πr_cl²
Surface area of cone = πr_co² + πr_col
Since we don’t require canvas for the top surface and bottom surface of cylinder and also for the base of cone we should subtract those areas from the surface area
Area of upper and lower surfaces of cylinder = 2πr_cl²
∴ Area of canvas required for cylinder = 2πr_clh + 2πr_cl² - 2πr_cl²
= 2πr_clh
= 2 × 3.14 × 51 × 4
= 1281.12 m²
Area of base of cone = πr_co²
∴ area of canvas required for cone = πr_co² + πr_col - πr_co²
= πr_col
= 3.14 × 51 × 40
= 6405.6 m²
Total area of canvas required = Area of canvas required for cylinder + area of canvas required for cone
= 1281.12 + 6405.6
= 7686.72 m²
∴ Total area of canvas required = 7686.72 m²

Q.4. The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm respectively. Find the curved surface area of the bucket.

Given: slant height of bucket = l = 45 cm
Radius of bottom circle = r = 7 cm
Radius of top circle = R = 28 cm
As the bucket is in the form of frustum
Formula: Total surface area of frustum = πr² + πR² + π(R + r)l cm²
Now we have asked curved surface area, so we should subtract the top and bottom surface areas which are flat circles.
Surface area of top = πr²
Surface area of bottom = πR²
∴ Curved surface area = total surface area – πr² - πR² cm²
= πr² + πR² + π(R + r)l – πr² - πR² cm²
= π(R + r)l cm²
= 3.14 × (28 + 7) × 45 cm²
= 3.14 × 35 × 45 cm²
= 4945.5 cm²
Therefore, curved surface area of bucket = 4945.5 cm².

Q.5. A solid metal cone with radius of base 12 cm and height 24 cm is melted to form solid spherical balls of diameter 6 cm each. Find the number of balls formed.

Given: base radius of cone = r_c = 12 cm
Height of cone = h = 24 cm
Diameter of spherical ball = 6 cm
Radius of spherical ball = r_s = 6/2 = 3 cm
Formula: volume of cone = (1/3)πr_c²h
Volume of sphere = (4/3)πr_s³
Let n be the number of spherical balls made
As the cone is melted and then the spherical balls are made therefore the volume remains same
i.e. volume of n spherical balls made = volume of cone
∴ n × (4/3) × π × r_s³ = (1/3) × π × r_c² × h
n × 4 × 3³ = 12² × 24
n × 9 = 12 × 24
n = 32
∴ Number of balls formed = 32

Q.6. A hemisphere bowl of internal diameter 30 cm is full of a liquid. This liquid is filled into cylindrical - shapes bottles each of diameter 5 cm and height 6 cm. How many bottles are required?

Given: diameter of hemisphere = 30 cm
∴ Radius of hemisphere = r_h = 30/2 = 15cm
Diameter of cylindrical shaped bottles = 5 cm
∴ radius of cylindrical shaped bottles = 5/2 = r_c = 2.5 cm
Height of cylindrical shaped bottle = h = 6 cm
Formula: volume of hemisphere = (volume of sphere/2) = (2/3)πr_h³
Volume of cylinder = πr_c²h
Let ‘n’ bottles are required
As we are filling the cylindrical bottles with liquid in hemispherical bowl hence we can say that volume of liquid in cylindrical bottles = volume of liquid in hemisphere
∴ n × π × r_c² × h = (2/3) × π × r_h³
n × 2.5² × 6 × 3 = 2 × 15³
n × 6.25 × 9 = 3375
n = 3375/56.25
n = 60
Therefore 60 cylindrical shaped bottles are required to fill the liquid from hemispherical bowl.

Q.7. A solid metallic sphere of diameter 21 cm is melted and recast into small cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.

Given: diameter of sphere = 21 cm
∴ radius of sphere = r_s = (21/2) cm
Diameter of cone = 3.5 cm
∴ radius of cone = r_c = 3.5/2 = 1.75 = (7/4) cm
Height of cone = h = 3 cm
Formula: volume of sphere = (4/3)πr_s³
Volume of cone = (1/3)πr_c²h
Sphere is melted and then cones are made from molten metal therefore the volume remains same
Let ‘n’ be the number of cones made
i.e. volume of n cones = volume of sphere
∴ n × (1/3) × π × r_c² × h = (4/3) × π × r_s³


Therefore number of cones formed = 504

Q.8. The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.

Given: diameter of sphere = 42 cm
∴ radius of sphere = 42/2 = r_s = 21 cm
Diameter of cylindrical wire = 2.8 cm
∴ Radius of cylindrical wire = r_c = 1.4 = (7/5)cm
Let l be the length of wire
Formula: volume of sphere = (4/3)πr_s³
Volume of wire = πr_c²l
Sphere is melted and wire is made from it
∴ volume of sphere = volume of wire
(4/3)πr_s³ = πr_c²l
4 × 21³ = 3 × (7/5)² × l
4 × 21 × 9 × 25 = 3 × l
2100 × 3 = l
l = 6300 cm
Therefore length of wire formed = 6300 cm = 63 meters

Q.9. A drinking glass is in the shape of frustum of a cone of height 21 cm with 6 cm and 4 cm as the diameters of its two circular ends. Find the capacity of the glass.

Given: Height of glass = h = 21 cm
Diameter of lower circular end of glass = 4 cm
Diameter of upper circular end of glass = 6 cm
∴ Radius of lower circular end = r = 4/2 = 2 cm
∴ Radius of upper circular end = R = 6/2 = 3 cm

Capacity of glass = volume of frustum

= 22 × (9 + 4 + 6)
= 22 × 19
= 418 cm³
∴ Capacity of glass = 418 cm³

Q.10. Two cubes, each of volume 64 cm³, are joined end to end. Find the total surface area of the resulting cuboid.

volume of each cube = 64 cm³
Let a be the side length of each cube
∴ a³ = 64
a = 4 cm
The figure shows both the cubes joined together after joining we get a cuboid of length 2a and breadth a and height a
Length of cuboid formed = l = 2a
l = 8 cm
Breadth of cuboid formed = b = 4 cm
Height of cuboid formed = h = 4 cm
In the cuboid so formed there are 4 rectangular surfaces of length l = 8 and breadth b = 4 and 2 square surfaces of length 4
Total surface area of cuboid = 4 × l × b + 2a²
= (4 × 8 × 4) + (2 × 4²)
= 128 + 32
= 160 cm²
Total surface area of cuboid = 160 cm²

Q.11. The radius of the base and the height of a solid right circular cylinder are in the ratio 2:3 and its volume is 1617 cm³. Find the total surface area of the cylinder. [Take π = 22/7.]

Given: volume of cylinder = 1617 cm³
Let r be the radius of base and h be the height of cone
r:h = 2:3
∴ r/h = 2/3
3r = 2h
h = 3r/2 …(i)
Formula: volume of cylinder = πr²h
∴ 1617 = (22/7) r²h
r²h = 514.5
Using (i) we have
∴ r² × (3r/2) = 514.5
3r³ = 1029
r³ = 343
r = 7 cm
h = 21/2 cm
Total surface area of cylinder = 2πr² + 2πrh
= 2 × (22/7) × 7² + 2 × (22/7) × 7 × (21/2)
= 308 + 462
= 770 cm²
Therefore total surface area of cylinder = 770 cm²

Q.12. A toy is in the form of a cone mounted on a hemisphere on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. find the total surface area of the toy.

Given: Height of toy = h = 31 cm
Radius of hemisphere = radius of base of cone = r = 7 cm
From the figure we can calculate height of cone as
Height of cone = h_c = h - r
= 31 - 7 = 24 cm
∴ h_c = 24 cm
Formula: surface area of hemisphere = surface area of sphere/2 = 2πr²
Curved surface area of cone = πrl
Where l is slant height

l = √(49 + 576) = 25 cm
∴ l = 25 cm
Total surface area of toy = curved surface area of cone + surface area of hemisphere
Surface area of hemisphere = 2 × π × r²
= 2 × (22/7) × 7²
= 308 cm²
Curved surface area of cone = π × r × l
= (22/7) × 7 × 25
= 550 cm²
∴ Total surface area of toy = 308 + 550
= 858 cm²
∴ Total surface area of toy = 858 cm²

Q.13. A hemispherical bowl of internal radius 9 cm is full of water. This water is to be filled in cylindrical bottles of diameter 3 cm and height 4 cm. find the number of bottles needed to fill the whole water of the bowl.

Given: Radius of hemisphere = r_h = 9 cm
Diameter of cylindrical shaped bottles = 3 cm
∴ radius of cylindrical shaped bottles = r_c = 3/2 = 1.5 cm
Height of cylindrical shaped bottle = h = 4 cm
Formula: volume of hemisphere = (volume of sphere/2) = (2/3)πr_h³
Volume of cylinder = πr_c²h
Let ‘n’ bottles are required
As we are filling the cylindrical bottles with liquid in hemispherical bowl hence we can say that volume of liquid in cylindrical bottles = volume of liquid in hemisphere
∴ n × π × r_c² × h = (2/3) × π × r_h³
n × (3/2)² × 4 × 3 = 2 × 9³
n = 3³ × 2
n = 27 × 2
n = 54
Therefore 54 cylindrical shaped bottles are required to fill the liquid from hemispherical bowl.

Q.14. The surface areas of a sphere and a cube are equal. Find the ratio of their volumes. [Takes π = 22/7.]

Let r be the radius of sphere and a be the side length of cube.
Let S_s be the surface area of sphere and S_c be the surface area of cube and V_s be volume of sphere and V_c be volume of cube
∴ S_s = 4πr² and S_c = 4a²
Given that surface area of sphere and cube are equal
∴ S_s = S_c
4πr² = 6a²
r²/ a² = 3/2π

V_s = (4/3) πr³
V_c = a³
∴ V_s/V_c = 4πr³/3a³
Using (i)

∴ V_s/V_c = √21/√11
Therefore ratio of their volumes is V_s:V_c = √21:√11.

Q.15. The slant height of the frustum of a cone is 4 cm and the perimeters (i.e. , circumferences) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.

Given: perimeter of upper circle = 18 cm
Perimeter of lower circle = 6 cm
Slant height of frustum = l = 4 cm
Formula: Total surface area of frustum = πr² + πR² + π(R + r)l cm²
Let r be the radius of lower circle and R be the radius of upper circle
Now perimeter of circle = circumference of circle = 2π × radius
∴ Perimeter of upper circle = 2πR
18 = 2 × π × R
R = 9/π cm
Perimeter of lower circle = 2πr
6 = 2 × π × r
r = 3/π cm
Now we have asked curved surface area, so we should subtract the top and bottom surface areas which are flat circles.
Surface area of top = πR²
Surface area of bottom = πr²
∴ Curved surface area = total surface area - πr² - πR² cm²
= πr² + πR² + π(R + r)l - πr² - πR² cm²
= π(R + r)l cm²
= π × [(9/π) + (3/π)] × 4 cm²
= (9 + 3) × 4 cm²
= 48 cm²
∴ curved surface area = 48 cm²

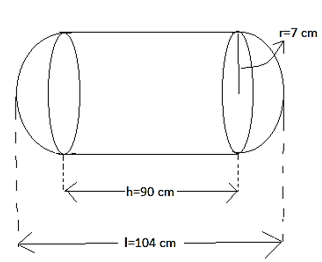
Q.16. A solid is composed of a cylinder with hemisphere ends. If the whole length of the solid is 104 cm and the radius of each hemispherical end is 7 cm, find the surface area of the solid.

Total length of solid = l = 104 cm as shown in figure
The solid consist of a cylinder and two hemispheres
Let the height of cylinder be h
We get the height h by subtracting the radii of left and right hemisphere from the total length l as seen in figure
∴ h = 104 - (7 + 7) cm
∴ h = 90 cm
Let r be the radius of hemisphere and the radius of cylinder
∴ r = 7 cm
There are two hemisphere one at left and one at right both of same radius r and two hemispheres make one sphere
Surface area of sphere = 4πr²
The flat circles i.e. the upper and lower circles of cylinder are not to be considered in the surface area of whole solid as they are covered by the hemispheres therefore for cylinder we will take its curved surface area
Curved surface area of cylinder = 2πrh
Surface area of solid = surface area of sphere + curved surface area of cylinder
= 4πr² + 2πrh
= 2 × (22/7) × 7 × (2 × 7 + 90)
= 44 × 104
= 4576 cm²
Therefore total surface area of solid = 4576 cm²

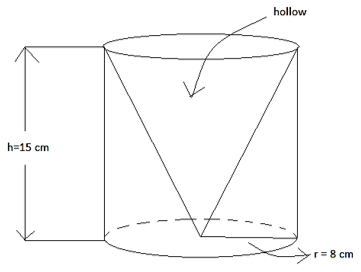
Q.17. From a solid cylinder whose height is 15 cm and diameter 16 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. [Use π = 3.14.]

After removing the conical solid the cylinder would look like this

Given: height of cylinder = height of cone = h = 15 cm
Diameter of cylinder = diameter of base cone = 16 cm
∴ radius of cylinder = radius of base of cone = 16/2 = r = 8 cm
Formula: total surface area of cylinder = 2πr² + πrh
Total surface area of cone = πrl + πr²
Where l is the slant height
l = √(r² + h²)
l = √(8² + 15²)
l = √289
l = 17 cm
In the solid as seen in figure we have the curved surface of cylinder and the base of cylinder as there is no top circular face of the cylinder we should subtract its area from total surface area of cylinder
Area of top circular surface of cylinder = πr²
∴ surface area of cylinder in solid = 2πr² + πrh - πr²
= πr² + πrh
= 3.14 × 8 × (8 + 15)
= 3.14 × 8 × 23
= 577.76 cm²
Now there is a hollow conical part with no base of the cone as seen in the figure therefore we should subtract the surface area of base of cone from the total surface area of cone
Surface area of base of cone = πr²
∴ Surface area of conical part in solid = πrl + πr² - πr²
= πrl
= 3.14 × 8 × 17
= 427.04 cm²
Therefore total surface area of solid = surface area of cylinder in solid + surface area of conical part in solid
= 577.76 + 427.04
= 1004.8 cm²
Surface area of solid = 1004.8 cm²

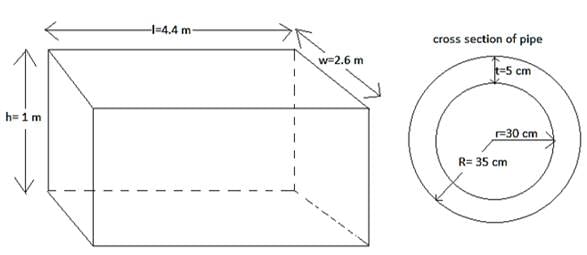
Q.18. A solid rectangular block of dimension 4.4 m, 2.6 m, 1 m is cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.

Given: length of the block = l = 4.4 m
Width of the block = w = 2.6 m
Height of the block = h = 1 m
Inner radius of pipe = r = 30 cm = 0.3 m
Thickness of pipe = t = 5 cm = 0.05 m
∴ outer radius of pipe as seen in the cross section of pipe = R = r + t = 30 + 5 = 35 cm = 0.35 m
Let l be the length of the pipe
Formula: volume of block = l × w × h
= 4.4 × 2.6 × 1
= 11.44 m³
Volume of block = 11.44 m³
Volume of pipe = π × (radius)² × (length)
Volume of pipe material = volume of full pipe(R = 0.35) – volume of hollow cylinder(r = 0.3)
= π × 0.35² × l - π × 0.3² × l
= π × l × [(35/100)² - (3/10)²]
= π × l × [(35/100) + (3/10)] × [(35/100) - (3/10)]

= (22/7) × l × (13/400) m³
∴ volume of pipe material = (22/7) × l × (13/400) m³
The pipe is made from the block
∴ volume of block = volume of pipe material
∴ 11.44 = (22/7) × l × (13/400)

∴ l = 28 × 4
∴ l = 112 m
Length of the pipe = 112 m

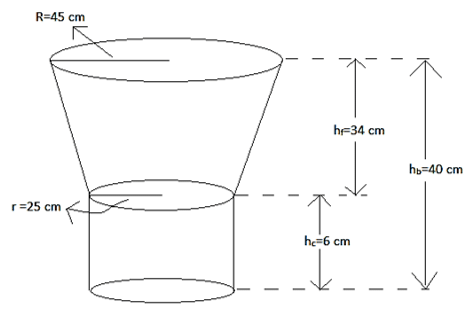
Q.19. An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The diameter of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket. Also, find the volume of water the bucket can hold, in litres.

Given: radius of upper circular end of frustum = R = 45 cm
Radius of lower circular end of frustum = radius of cylindrical base = r = 25 cm
Height of bucket = h_b = 40 cm
Height of cylindrical base = h_c = 6 cm
From the figure height of frustum = h_f = h_b - h_c
= 40 - 6
∴ h_f = 34 cm

Volume of cylinder = πr²h_c
Curved surface area of cylinder = 2πrh_c
curved surface area of frustum = π(R + r)l cm²
Where l = slant height


= √(400 + 1156)
= 39.44 cm
Area of metallic sheet used = curved surface area of frustum + curved surface area of base cylinder + area of base circle of cylinder
Now, curved surface area of frustum = π × (R + r) × l cm²
= (22/7) × (45 + 25) × 39.44 cm²
= 22 × 10 × 39.44 cm²
= 8676.8 cm²
Curved surface area of base cylinder = 2πrh_c
= 2 × (22/7) × 25 × 6
= 942.85 cm²
Surface area of base circle of cylinder = πr²
= (22/7) × 25²
= 1964.28 cm²
∴ Area of metallic sheet used = 8676.8 + 942.85 + 1964.28
= 11583.93 cm²
Therefore, area of metallic sheet used to make the bucket is 11583.93 cm² i.e. 1.158393 m²
Volume of water bucket can hold = volume of bas cylinder + volume of frustum
Volume of base cylinder = πr²h_c
= (22/7) × 25² × 6
= 11785.71 cm³


= 35.62 × 3775
= 134465.5 cm³
∴ volume of water bucket can hold = 11785.71 + 134465.5
= 146251.21 cm³
Now 1 litre is 1000 cm³
∴ 146251.21 cm³ = 146251.21/1000 = 146.25121 litres
Volume of water bucket can hold = 146.25121 litres

Q.20. A farmer connect a pipe of internal diameter 20 cm from a canal into a cylindrical tank which is 10 m diameter and 2 m deep. If the water flows through the pipe at the of 4 km/hr, in how much time will the tank be filled completely?

Given: diameter of pipe = 20 cm
∴ radius of pipe = r_p = 20/2 = 10 cm = 0.1 m
Diameter of tank = 10 m
∴ radius of cylindrical tank = r_c = 10/2 = 5 m
Depth of cylindrical tank = height of cylindrical tank = h = 2 m
Rate of flow of water through pipe = 4 km/hr
1 km = 1000 m
4 km/hr = 4000 m/hr
Volume of water required to completely fill the tank is equal to the volume of cylinder
Time require to fill the tank = volume of cylindrical tank/volume of water flown through pipe per hr volume of cylindrical tank = π × r_c² × h
= 3.14 × 25 × 2
= 157 m³
volume of water flown through pipe per hr = π × r_p² × 4000
= 3.14 × 0.1² × 4000
= 3.14 × 40
= 125.6 m³/hr
Time require to fill the tank = 157/125.6
= 1.25 hrs
Therefore, it will take 1.25 hours to fill the tank completely.