Raoult's Law | Chemistry Class 12 - NEET PDF Download
| Table of contents |

|
| Who discovered Raoult's Law? |

|
| What is Raoult’s Law? |

|
| Finding Vapour Composition |

|
| Raoult's Law as a special case of Henry's law |

|
| Limitations of Raoult’s Law |

|
| Solved Examples |

|
Who discovered Raoult's Law?
- Raoult’s law has been named after François-Marie Raoult, a French chemist who while experimenting found out that when substances were mixed in a solution, the vapour pressure of the solution decreased simultaneously.
- Raoult’s law was established in 1887 and is also considered the law of thermodynamics.
What is Raoult’s Law?
Raoult’s law states that:
For a solution of volatile liquids, the partial vapour pressure of each component of the solution
is directly proportional to its mole fraction present in solution.
Mathematical representation of Raoult’s law:
Let's understand this by looking at the example below
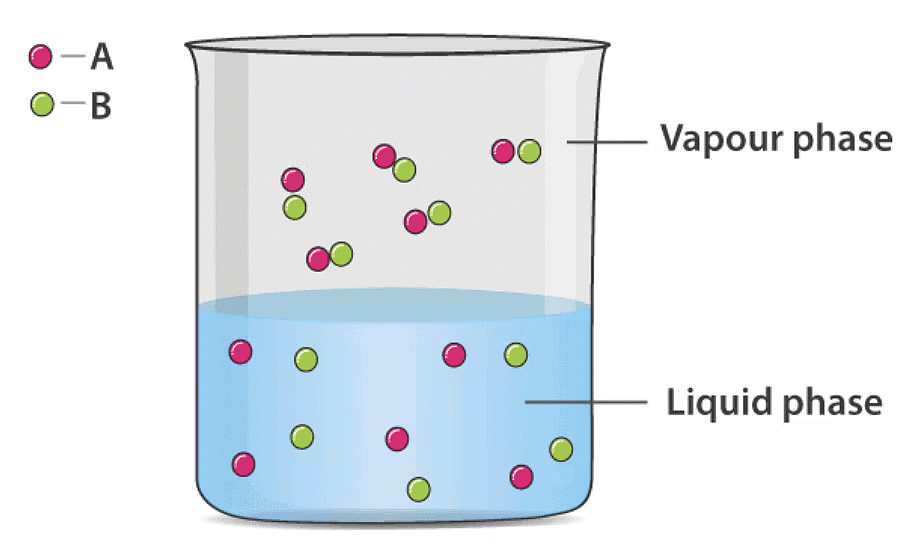 Ideal Solution of Two Volatile Liquids
Ideal Solution of Two Volatile Liquids
Let two volatile liquids A and B dissolve each other to form an ideal solution. Then the vapours above the solution will contain the vapours of A and B. Applying Dalton’s law of partial pressure the total vapour pressure of the solution will be
Psolution = PA + PB
Where,
PA and PB are the partial vapour pressures of A and B.
PA = PºA XA
PB = PºB XB
Where:
- PºA and PºB are vapour pressures of pure A and B respectively
- xA and xB are mole fractions of A and B in a liquid solution respectively
Hence, 𝑃 (Solution) 𝑜𝑟 Ps = PA0 XA + PB0 XB
Also, Ps = P0A(1-XB) + P0BXB
⇒ Ps = P0A+(P0B - P0A)XB
This equation is of the form y = mx + c. The value of m (slope) may be (+ve) or (–ve) depending upon whether P0B > P0A (m = + ve) or P0B < P0A (m = –ve).
Hence a plot of a graph of Ps versus XB will be a straight line with an intercept on the y-axis equal to pA and a slope equal to (P0B - P0A)
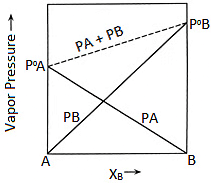 Plot of Vapour Pressure and Mole Fraction
Plot of Vapour Pressure and Mole Fraction
The total Pressure of a Solution will be:
- P (Solution) = PA + PB = xAP0A + xBP0B
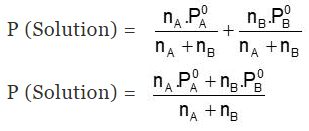
Finding Vapour Composition
- Vapour composition means to find out the mole fraction of A and B in vapour i.e yA and yB.
- Dalton’s law of particle pressure is used to calculate the vapour composition, as we know, Partial pressure = mole fraction × total pressure
⇒ pA= yA × pS
or yA =𝑃A/𝑃𝑆
Similarly for B
⇒ yB = 𝑃A/𝑃𝑆
where yA and yB are mole fractions of ‘A’ and ‘B’ in the vapour phase and yA + yB = 1
SPECIAL NOTE:
xA and xB are mole fraction of ‘A’ and ‘B’ in the solution phase and xA + xB =1yA and yB are mole fraction of ‘A’ and ‘B’ in the vapour phase and yA + yB =1
Raoult's Law as a special case of Henry's law
- At a given temperature liquids vaporize. At equilibrium, the pressure exerted by the vapour of the liquid over the liquid phase is referred to as vapour pressure.
- According to Raoult’s law, the vapour pressure of a volatile component in a given solution can be defined by pi = pi˚xi
- In an answer of a gas in a fluid one of the segments is volatile to the point that it exists as a gas and solvency is given by Henry's law which expresses that p = KH x
- Comparing both the equations we get that partial pressure of the volatile component or gas is directly proportional to its mole fraction in solution. The proportionality constant KH differs from pi˚
- Therefore, Raoult's law turns into a unique instance of Henry’s law in which KH get to be equivalent to pi˚
Limitations of Raoult’s Law
There are a few limitations to Raoult’s law:
- Raoult’s law is apt for describing ideal solutions. However, ideal solutions are hard to find and they are rare. Different chemical components have to be chemically identical equally.
- Since many of the liquids that are in the mixture do not have the same uniformity in terms of attractive forces, these type of solutions tends to deviate away from the law.
There is either a negative or a positive deviation:
- Negative deviation happens when the vapour pressure is lower than what Raoult's law predicts. For instance, this occurs in a mix of chloroform and acetone or in a solution of water and hydrochloric acid.
- On the other hand, positive deviation occurs when the attraction among similar molecules is stronger, surpassing the attraction between dissimilar molecules. In such cases, both components of the mixture can easily evaporate from the solution. An example of positive deviation is seen in mixtures like benzene and methanol or ethanol and chloroform.
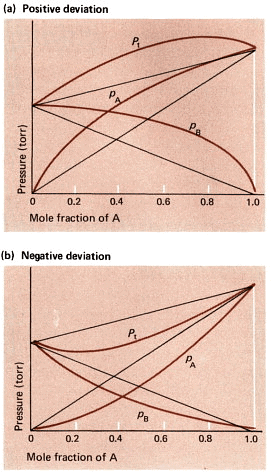 Positive and Negative Deviation
Positive and Negative Deviation
Solved Examples
Example 1. The vapour pressure of ethanol and methanol are 44.5 mm and 88.7 mm Hg respectively. An ideal solution is formed at the same temperature by mixing 60 g of ethanol with 40g of methanol. Calculate the total vapour pressure of the solution.
Solution.
Number of moles of ethanol = 60/40 = 1.5
Number of moles of methanol = 40/32 = 1.25
XA = 1.25/1.25 + 1.3 = 0.4545 and XB = 1 – 0.4545 = 0.545
Let A = CH3OH, B = C2H5OH
Total pressure of the solution
PT = XAP0A + XBP0B
= 0.4545 × 88.7 + 0.545 × 44.5 = 40.31 + 24.27
= 64.58 mm Hg
Example 2. The composition of vapour over a binary ideal solution is determined by the composition of the liquid. If XA and YA are the mole fraction of A in the liquid and vapour, respectively find the value of XA for which YA − XA has a minimum. What is the value of the pressure at this composition?
Solution. 
Subtracting xA from both sides, we get
Now differentiating w.r.t. xA, we get
The value of xA at which yA − xA has a minimum value can be obtained by putting the above derivative equal to zero. Thus we have
Solving for xA, we get
hence
Example 3. A very small amount of non-volatile solute (that does not dissociate) is dissolved in 56.8 cm3 of benzene (density 0.889 g cm-3). At room temperature, the vapour pressure of this solution is 99.88 mm Hg while that of benzene is 100mm Hg. Find the molality of this solution. If the freezing temperature of this solution is 0.73 degrees lower than that of benzene. What is the value of the molal freezing point depression constant of benzene?
Solution.
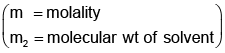
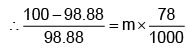
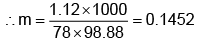
Also,
ΔTf = Kf × molality f
∴ 0.73 = K × 0.1452
fK = 5.028 K. molality
Example 4. What is the composition of the vapour which is in equilibrium at 30°C with a benzene-toluene solution with a mole fraction of benzene of 0.400?
(PoB = 119 torr and PTo = 37.0 torr)
Solution.
The Total pressure of the solution is given by
PT = XB P0B + XTP0T
= 0.4 × 119 + 0.6 × 37
= 47.6 + 22.2
= 69.8 torr
Applying Dalton’s law for mole fraction in the vapour phase.
YB = PB/PT = 47.6/62.4
= 0.763
YT = 1– 0.763
= 0.237
|
75 videos|278 docs|78 tests
|
FAQs on Raoult's Law - Chemistry Class 12 - NEET
| 1. Who discovered Raoult's Law? |  |
| 2. What is Raoult’s Law? |  |
| 3. How can we find vapor composition using Raoult's Law? |  |
| 4. How is Raoult's Law related to Henry's Law? |  |
| 5. What are the limitations of Raoult’s Law? |  |
















