Ratio And Proportion | Quantitative Techniques for CLAT PDF Download

Ratio

In certain situations, the comparison of two quantities by the method of division is very efficient. We can say that the comparison or simplified form of two quantities of the same kind is referred to as a ratio. This relation gives us how many times one quantity is equal to the other quantity. In simple words, the ratio is the number that can be used to express one quantity as a fraction of the other ones.
The two numbers in a ratio can only be compared when they have the same unit. We make use of ratios to compare two things. The sign used to denote a ratio is ‘:’.

A ratio can be written as a fraction, say 2/5. We happen to see various comparisons or say ratios in our daily life.
Hence, the ratio can be represented in three different forms, such as:

• a to b
• a : b
• a/b

Notes

• The ratio should exist between the quantities of the same kind.
• While comparing two things, the units should be similar.
• There should be significant order of terms.
• The comparison of two ratios can be performed, if the ratios are equivalent like the fractions.

Proportion

Proportion is an equation that defines that the two given ratios are equivalent to each other. In other words, the proportion states the equality of the two fractions or the ratios. In proportion, if two sets of given numbers are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other.

For example, the time taken by train to cover 100km per hour is equal to the time taken by it to cover the distance of 500km for 5 hours. Such as 100km/hr = 500km/5hrs.
Ratio and proportions are said to be faces of the same coin. When two ratios are equal in value, then they are said to be in proportion. In simple words, it compares two ratios. Proportions are denoted by the symbol  ‘::’ or ‘=’.
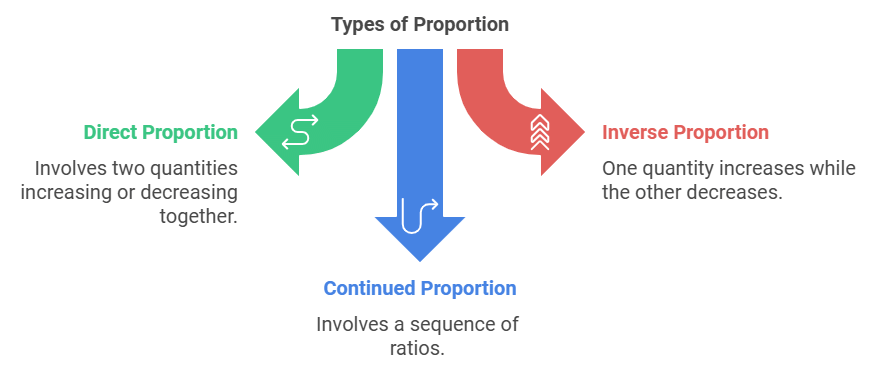
The proportion can be classified into the following categories, such as:

• Direct Proportion
• Inverse Proportion
• Continued Proportion

Direct Proportion

The direct proportion describes the relationship between two quantities, in which the increases in one quantity, there is an increase in the other quantity also. Similarly, if one quantity decreases, the other quantity also decreases. Hence, if “a” and “b” are two quantities, then the direction proportion is written as a ∝ b.

Inverse Proportion

The inverse proportion describes the relationship between two quantities in which an increase in one quantity leads to a decrease in the other quantity. Similarly, if there is a decrease in one quantity, there is an increase in the other quantity. Therefore, the inverse proportion of two quantities, say “a” and “b” is represented by a ∝ (1/b).

Continued Proportion

Consider two ratios to be a : b and c : d.
Then in order to find the continued proportion for the two given ratio terms, we convert the means to a single term/number. This would, in general, be the LCM of means.
For the given ratio, the LCM of b & c will be bc.
Thus, multiplying the first ratio by c and the second ratio by b, we have
First ratio- ca : bc
Second ratio- bc : bd
Thus, the continued proportion can be written in the form of ca : bc : bd

Ratio Formula

Assume that, we have two quantities (or two numbers or two entities) and we have to find the ratio of these two, then the formula for ratio is defined as;
a : b ⇒ a/b
where a and b could be any two quantities.
Here, “a” is called the first term or antecedent, and “b” is called the second term or consequent.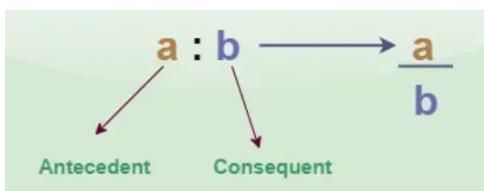
Example: In ratio 4 : 9, is represented by 4/9, where 4 is antecedent and 9 is consequent.
If we multiply and divide each term of ratio by the same number (non-zero), it doesn’t affect the ratio.
Example: 4 : 9 = 8 : 18 = 12 : 27

Proportion Formula

Now, let us assume that, in proportion, the two ratios are a:b & c:d. The two terms ‘b’ and ‘c’ are called ‘means or mean term,’ whereas the terms ‘a’ and ‘d’ are known as ‘extremes or extreme terms.’
a/b = c/d or a : b :: c : d
Example: Let us consider one more example of a number of students in a classroom. Our first ratio of the number of girls to boys is 3:5 and that of the other is 4:8, then the proportion can be written as:
3 : 5 ::  4 : 8 or 3/5 = 4/8
Here, 3 & 8 are the extremes, while 5 & 4 are the means.

Note: The ratio value does not affect when the same non-zero number is multiplied or divided on each term.

Difference Between Ratio and Proportion

Some Useful Results on Proportion 

If a, b, c and d are four quantities. then,
(i) a:b :: c:d means b:a :: d:c  (invertendo)
(ii) a:b :: c:d means a:c :: b:d (Alternando)
(iii) a:b :: c:d means (a+b) : b :: (c+d) : d (Componendo)
(iv) a:b :: c:d means (a - b) : b :: (c - d) :d (dividendo)
(v) If a:b :: c:d then (a + b) : (a – b) :: (c + d) : (c – d) (componendo and dividendo)
(vi) If a:b :: c:d then a: (a – b) :: c : (c – d) (convertendo)

Some Useful Result for Proportional Division

• The process of dividing a given quantity into parts which are proportional to a given ratio is called proportional division and the resultant quantities obtained are called proportional parts. 
• For example: If 240 is to be divided in the ratio 3:4:5 60, 80 and 100 will be the proportional part since the ratio of these quantities is 3:4:5 and their sum is 240.

Method of Finding Proportional Part

If a quantity P is to be divided in the ratio of a:b:c and the resultant proportional parts are x, y and z then,
x = ka, y = kb and z = kc
Now, P = x + y +z
or ka + kb + kc = P
or
Proportional part

So, to calculate the proportional parts:
(a) Given quantity is divided by the sum of ratios.
(b) The quotient so obtained is multiplied by the respective numbers of the given ratio.
(c) The resultants will be the required proportional parts.
For example: Divide 2700 in the ratio 2:3:4
Sum of the ratio = 2 + 3 + 4 = 9
First part =  = 300 x 2 = 600
Second part =  = 300 x 3 = 900
Third part = = 300 x 4 = 1200

Example 1: If 38% of A = 52% of B then A : B = ?
Solution: It means A x
or 38 A = 52 B or  . So A : B = 26:19

Example 2: The salaries of A, B and C are in the ratio 3:5:7. If their salaries are increased by 50%, 60% and 50% respectively, the ratio between new salaries is
Solution: After increase of 50% Salary of A is 3 X
After increase of 60% of salary of B is =
After increase of 50% salary of C is
Ratio between the new salaries of A, B and C is

or 45:80:105      or 9:16:21

Example 3: The speed of three Cars is in the ratio of 3:4:5. The ratio between the time taken by them to travel a fixed distance is
Solution: Let fixed distance be d  
Time taken by first car is
Time taken by second car is
Time taken by 3^rd car is =
So ratio of time between three cars is

or ratio is  

or
20 : 15 : 12

Example 4: A mixture contains alcohol and water in the ratio 3:2. On adding 5 litre of water in it, the quantities of alcohol and water become equal. What is the quantity of alcohol in the mixture.
Solution: Ratio of alcohol to water is 3 : 2. If 3 litre is alcohol then 2 litre is water
If we add one litre of water the quantity of alcohol and water become equal
So if on adding 1 litre of water quantities become equal then quantity of alcohol is 3 litre
If on adding 5 litre they become equal then alcohol is 3 x 5 = 15 litre.

Example 5:Two metals contain zinc and copper in the ratio 2:1 and 4:1 respectively. In what ratio these two must be mixed to get a new metal containing zinc and copper in the ratio 3 : 1
Solution: By the method of allegation and mixture

By the method of allegation and mixture:
The reqd. ratio is
Or 3:5 [multiply by 60]

Example 6: Mean proportional between 104 and 234 is
Solution:  Mean proportional is
= 2 x 2 x 3 x 13 = 156

Example 7: There are three partners A, B and c in a firm. A’s capital is equal to thrice of B’s and B’s capital is 4 times C’s capital. Find the ratio of the capital of A, B and C
Solution: Given is A = 3B
and B = 4c
so A = 3B = 3 x 4c
So
So Ratio of A : B : C is 12 : 4 : 1

Example 8: In a mixture of 75 litres, the ratio of milk to water is 2:1. How much water should be added in the mixture so that the ratio of milk to water is 1 : 2
Solution: Ratio of milk to water is 2 : 1
In 75 litres milk is 50 and water is 25 i.e. 50:25
We want to make the ratio as 1 : 2 i.e 50 : 100.
Since the milk in two ratios is 50 each and we want to convert 25 water to 100 water. So 75 litres of water be add.