Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Rearranging Formulae
Rearranging Formulae | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Simple Rearranging
What are formulae?
- A formula (plural, formulae) represents a mathematical relationship involving variables, constants, and an equals sign.
- In your IGCSE studies, you will encounter various formulae, such as those for areas and volumes of shapes, equations of lines and curves, and the correlation between speed, distance, and time.
- Examples of formulae you should recognize include:
- The equation of a straight line
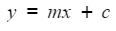
- The area of a trapezium
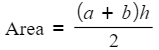
- Pythagoras' theorem
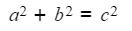
- The equation of a straight line
- You will also be tasked with rearranging unfamiliar formulae.
How do I rearrange formulae where the subject appears only once?
- The subject is the variable that you want to find out, or get on its own on one side of the formula
- The method for changing the subject is the same as the method used for solving linear equations
- STEP 1: Remove any fractions or brackets
- Remove fractions by multiplying both sides by anything on the denominator
- Expand any brackets only if it helps to release the variable; if not, it may be easier to leave the bracket there
- STEP 2: Carry out inverse operations to isolate the variable you are trying to make the subject
- This works in the same way as with linear equations, however, you will create expressions rather than carry out calculations
- For example, to rearrange
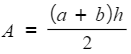 so that h is the subject
so that h is the subject- Multiply by 2
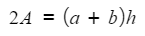
- Expanding the bracket will not help here as we would end up with the subject appearing twice, so instead divide by the whole expression (a + b)
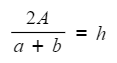
- You can now rewrite this with the subject (h) on the left hand side
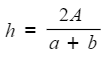
- Multiply by 2
How do I rearrange formulae that include powers or roots?
- If the formula contains a power of n, use the nth root to reverse this operation
- For example to make x the subject of y = ax5
- Divide both sides by a first
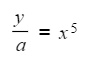
- Then take the 5th root of both sides
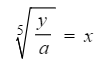
- Divide both sides by a first
- For example to make x the subject of y = ax5
- If n is even then there will be two answers: a positive and a negative
- For example if
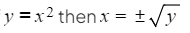
- For example if
- If the formula contains an nth root, reverse this operation by raising both sides to the power of n
- For example to make a the subject of
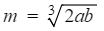
- Raise both sides to the power of 3 first
m3 = 2ab - Divide both sides by 2b
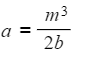
- Raise both sides to the power of 3 first
- For example to make a the subject of
Are there any common formulae to be aware of?
- The formula for the equation of a straight line is often used
y = mx + c - Formulae for accelerating objects are often used
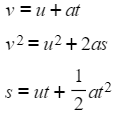
- The letters mean the following:
- t stands for the amount of time something accelerates for (in seconds)
- u stands for its initial speed (in m/s) - the speed at the beginning
- v stands for its final speed (in m/s) - the speed after t seconds
- a stands for its acceleration (in m/s2) during in that time
- s stands for the distance covered in t seconds
- You do not need to memorise these formulae, but you should know how to substitute numbers into them
- The letters mean the following:
Subject Appears Twice
How to Rearrange Formulas where the Subject Appears Twice?
- If the subject appears twice, you will need to factorize the equation. Factorizing involves placing an expression into brackets, with the subject positioned outside the brackets.
- Factorizing entails enclosing an expression in brackets, with the subject situated outside the brackets.
- In scenarios where the subject is enclosed within a set of brackets, you must expand these brackets before proceeding with rearrangements.
- If the subject is present on both sides of a formula, you must consolidate those terms onto the same side before factorizing.
The document Rearranging Formulae | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|413 docs|19 tests
|
FAQs on Rearranging Formulae - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the importance of rearranging formulae in algebra and sequences? |  |
Ans. Rearranging formulae allows us to isolate a specific variable in an equation, making it easier to solve for that variable. This skill is essential in mathematics as it helps us manipulate equations to find unknown values.
| 2. How can we rearrange formulae with powers or roots? |  |
Ans. When rearranging formulae with powers or roots, we can use inverse operations such as raising both sides of the equation to a power or taking the square root of both sides to isolate the variable.
| 3. Can you explain the step-by-step process for rearranging equations? |  |
Ans. The step-by-step process for rearranging equations involves identifying the variable you want to isolate, performing inverse operations to move terms to the other side of the equation, and simplifying the equation until the variable is on its own.
| 4. What are some common mistakes to avoid when rearranging formulae? |  |
Ans. Common mistakes to avoid when rearranging formulae include not applying inverse operations correctly, forgetting to perform the same operation on both sides of the equation, and not simplifying the equation fully.
| 5. How can expanding brackets help in rearranging formulae? |  |
Ans. Expanding brackets can help in rearranging formulae by distributing terms and simplifying the equation, making it easier to isolate variables and solve for unknown values.
Related Searches
















