Regular Expression to DFA | Theory of Computation - Computer Science Engineering (CSE) PDF Download
| Table of contents |

|
| Finite automata |

|
| Rules for Conversion of Regular Expression to NFA |

|
| Ɛ –closure |

|
| Sub-set Construction |

|
| Direct Method |

|
| Computation of followpos |

|
Finite automata
Language Recognizer: A program that accepts a string x and determines whether x is a sentence in a particular language, responding with "yes" or "no".
Regular Expression to Recognizer Conversion: This involves creating a Finite Automaton (FA) from a regular expression to function as a recognizer.
Finite Automata (FA): Finite Automata can be either:
- Non-deterministic Finite Automata (NFA): Characterized by multiple transitions for a single input symbol from a state, including transitions on an empty string (Ɛ).
- Deterministic Finite Automata (DFA): Defined by a single transition for each state and input symbol combination.
Components of Finite Automata: Represented as M=(Q,Σ,q0,F,δ), where:
- Q is the Set of states.
- Σ is the Set of input symbols.
- q0 is the Start state.
- F is the Set of final states.
- δ is the Transition function, mapping states to input symbols, represented as
δ:Q×Σ→Q.
Regular Expression to DFA Conversion Methods:
- Thompson’s Subset Construction:
- Converts a given regular expression into an NFA.
- Then transforms the resultant NFA into a DFA.
- Direct Method:
- Directly converts a given regular expression into a DFA.
- Thompson’s Subset Construction:
Rules for Conversion of Regular Expression to NFA
Union in Regular Expressions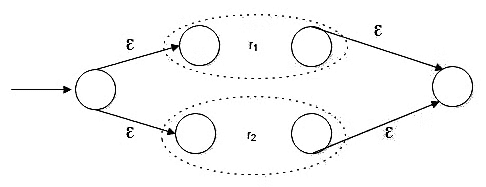
- Expressed as r=r1+r2.
- Represents the union operation, where r is a regular expression that matches either r1 or r2.
Concatenation in Regular Expressions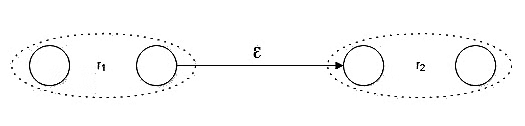
- Denoted by r=r1r2.
- Signifies the concatenation operation, where r is a regular expression that matches the sequence of r1 followed by r2.
Closure in Regular Expressions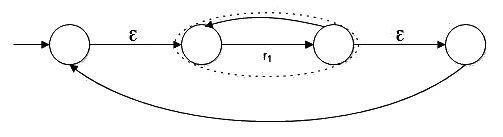
- Indicated as r=r1∗.
- Refers to the closure operation, where r is a regular expression that matches zero or more consecutive occurrences of r1.
Ɛ –closure
Ɛ-Closure Definition:
Ɛ-Closure refers to the set of states in a Non-deterministic Finite Automaton (NFA) that can be reached from a given state by traversing paths that consume the empty string (Ɛ). It describes the transitions that occur without consuming any input symbol.
Examples of Ɛ-Closure:
Example 1: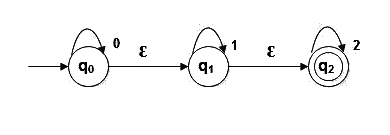
- Ɛ-Closure(q0) = { q0, q1, q2 }: From state q0, states q0, q1, and q2 are reachable by paths that consume an empty string.
- Ɛ-Closure(q1) = { q1, q2 }: From state q1, states q1 and q2 are reachable by paths that consume an empty string.
- Ɛ-Closure(q2) = { q0 }: From state q2, state q0 is reachable by a path that consumes an empty string.
Example 2: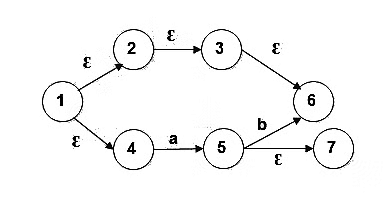
- Ɛ-Closure(1) = {1, 2, 3, 4, 6}: From state 1, states 1, 2, 3, 4, and 6 are reachable by paths that consume an empty string.
- Ɛ-Closure(2) = {2, 3, 6}: From state 2, states 2, 3, and 6 are reachable by paths that consume an empty string.
- Ɛ-Closure(3) = {3, 6}: From state 3, states 3 and 6 are reachable by paths that consume an empty string.
- Ɛ-Closure(4) = {4}: From state 4, state 4 is reachable by a path that consumes an empty string.
- Ɛ-Closure(5) = {5, 7}: From state 5, states 5 and 7 are reachable by paths that consume an empty string.
- Ɛ-Closure(6) = {6}: From state 6, state 6 is reachable by a path that consumes an empty string.
- Ɛ-Closure(7) = {7}: From state 7, state 7 is reachable by a path that consumes an empty string.
Sub-set Construction
Initial NFA Creation: Begin by transforming the given regular expression into a Non-deterministic Finite Automaton (NFA). This is achieved by applying standard rules for operators like union, concatenation, and closure, while respecting their precedence.
Epsilon-Closure Identification: Determine the epsilon-closure (Ɛ-closure) for every state in the NFA. The epsilon-closure of a state includes the state itself and any states that can be reached from it through epsilon transitions (transitions that don’t consume any input symbol).
Starting with Epsilon-Closure: Consider the epsilon closure of the NFA’s starting state as your initial point.
Transition Function Application: For each state and input symbol, apply the transition function. This involves moving from a state using an input symbol and then finding the epsilon-closure of the resulting state. The formula for the transition function in a Deterministic Finite Automaton (DFA) is: Dtran[state, input symbol] = Ɛ-closure(move(state, input symbol)), where Dtran represents the DFA's transition function.
State Analysis: After applying the transition function, analyze the resultant state to ascertain if it is a newly encountered state in the context of the DFA.
Iterative State Exploration: If a new state is discovered, continue applying steps 4 and 5 iteratively until no further new states emerge.
Transition Table Construction: Create a transition table for the DFA's transition function (Dtran), which maps combinations of states and input symbols to resulting states.
DFA Transition Diagram: Finally, draw the transition diagram for the DFA. This diagram should start from the epsilon-closure of the NFA’s starting state and conclude at a final state, which includes the NFA’s final state.
These steps systematically guide the conversion from a regular expression to a DFA, ensuring a thorough and accurate process.
 |
Download the notes
Regular Expression to DFA
|
Download as PDF |
Direct Method
- Direct Conversion Method: The direct method is employed to transform a given regular expression straight into a Deterministic Finite Automaton (DFA), bypassing the intermediate step of creating a Non-deterministic Finite Automaton (NFA).
- Augmented Regular Expression: This process utilizes an augmented regular expression, denoted as r#, to facilitate the conversion.
- NFA States and Regular Expression Positions: In this method, the significant states of the corresponding NFA are associated with positions in the regular expression that contain alphabet symbols.
- Syntax Tree Representation: The regular expression is represented as a syntax tree. In this tree, interior nodes correspond to operators that signify union, concatenation, and closure operations.
- Leaf Nodes: The leaf nodes of the syntax tree represent the input symbols of the regular expression.
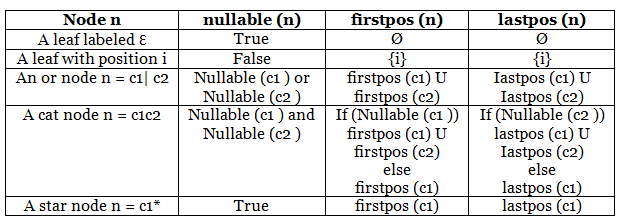
- Direct DFA Construction: The DFA is constructed directly from the regular expression by calculating specific functions from the syntax tree. These functions are nullable(n), firstpos(n), lastpos(n), and followpos(i).
- Nullable Function: The nullable(n) function is true for nodes marked with an asterisk (*) and for nodes labeled with epsilon (Ɛ). For all other nodes, this function is false.
- Firstpos Function: The firstpos(n) function is a set of positions at node 'n' that correspond to the first symbol of the sub-expression rooted at 'n'.
- Lastpos Function: The lastpos(n) function identifies a set of positions at node 'n' that correspond to the last symbol of the sub-expression rooted at 'n'.
- Followpos Function: The followpos(i) function determines a set of positions that follow a given position, matching the first or last symbol of a string generated by the sub-expression of the regular expression.
- Computational Rules: There are specific rules for computing the functions nullable, firstpos, and lastpos, which are vital for this direct conversion process.
- Rules for computing nullable, firstpos and lastpos
Computation of followpos
Rule for Concatenation (Cat) Nodes:
- In a syntax tree, if 'n' represents a concatenation (cat) node with a left child 'c1' and a right child 'c2', then a specific relationship between their positions is established.
- For every position 'i' that is in the lastpos(c1), which means the set of positions corresponding to the last symbol of the sub-expression rooted at the left child 'c1', every position in firstpos(c2) will be included in followpos(i).
- This rule implies that in a concatenation node, each position 'i' in the last set of positions of its left child directly leads to (or is followed by) all the positions in the first set of positions of its right child.
Rule for Star (*) Nodes:
- When dealing with a star (*) node, denoted as 'n', a different rule applies.
- If 'i' is a position in lastpos(n), meaning it's in the set of positions corresponding to the last symbol of the sub-expression rooted at the star node, then all positions in firstpos(n) are included in followpos(i).
- Essentially, this rule states that for a star node, the set of positions at the beginning (firstpos) of that node will be in the follow set (followpos) of every position in the last set (lastpos) of that node.
These rules are essential for understanding the relationship between different positions in a regular expression, particularly in the context of constructing a DFA directly from a regular expression's syntax tree. They define how positions are linked in the context of concatenation and closure operations within the regular expression.
|
18 videos|70 docs|44 tests
|
FAQs on Regular Expression to DFA - Theory of Computation - Computer Science Engineering (CSE)
| 1. What is a regular expression? |  |
| 2. What is the role of regular expressions in Computer Science Engineering (CSE)? |  |
| 3. How can regular expressions be converted into DFA (Deterministic Finite Automaton)? |  |
| 4. What are the advantages of using regular expressions in CSE? |  |
| 5. Can regular expressions be used for more than just string manipulation? |  |























