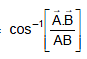Resolution of Vectors: Motion in a Plane | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Resolution of Vectors |

|
| Procedure to solve the Vector Equation |

|
| Addition and Subtraction in Component Form |

|
| Multiplication of Vectors (The Scalar and vector products) |

|
Resolution of Vectors
If  and
and  be any two non-zero vectors in a plane with different directions and
be any two non-zero vectors in a plane with different directions and  be another vector in the same plane.
be another vector in the same plane.  can be expressed as a sum of two vectors-one obtained by multiplying by a real number and the other obtained by multiplying by another real number.
can be expressed as a sum of two vectors-one obtained by multiplying by a real number and the other obtained by multiplying by another real number.

 (where l and m are real numbers)
(where l and m are real numbers)
We say that  has been resolved into two component vectors namely
has been resolved into two component vectors namely
 (where l and m are real number)
(where l and m are real number)
We say that  has been resolved into two component vectors namely
has been resolved into two component vectors namely

 and
and  along
along  and
and  respectively. Hence one can resolve a given vector into two component vectors along a set of two vectors - all the three lie in the same plane.
respectively. Hence one can resolve a given vector into two component vectors along a set of two vectors - all the three lie in the same plane.
Resolution along rectangular component
It is convenient to resolve a general vector along axes of a rectangular coordinate system using vectors of unit magnitude, which we call as unit vectors.  are unit along x, y and z-axis as shown in figure below :
are unit along x, y and z-axis as shown in figure below :

Resolution in two Dimensions
Consider a vector  that lies in xy plane as shown in figure,
that lies in xy plane as shown in figure,
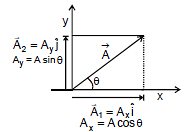

 ⇒
⇒ 
The quantities Ax and Ay are called x-and y-components of the vector  .
.
Ax is itself not a vector but  is a vector and so it
is a vector and so it  .
.
Ax = A cosθ and Ay = A sinθ
It's clear from above equation that a component of a vector can be positive, negative or zero depending on the value of q. A vector  can be specified in a plane by two ways :
can be specified in a plane by two ways :
(a) its magnitude A and the direction q it makes with the x-axis; or
(b) its components Ax and Ay A =  , θ =
, θ = 
Note : If A = Ax ⇒ Ay = 0 and if A = Ay ⇒ Ax = 0 i.e., components of a vector perpendicular to itself is always zero. The rectangular components of each vector and those of the sum  are shown in figure.
are shown in figure.

We saw that
 is equivalent to both
is equivalent to both
Cx = Ax + Bx
and Cy = Ay + By
Refer figure (b)
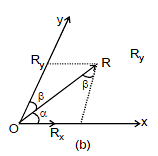
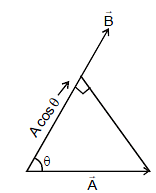
Vector  has been resolved in two axes x and y not perpendicular to each other. Applying sine law in the triangle shown, we have
has been resolved in two axes x and y not perpendicular to each other. Applying sine law in the triangle shown, we have

or Rx =  and Ry =
and Ry = 
If α+β = 90°, Rx = R sinβ and Ry = R sin
Ex.7 Resolve the vector  along an perpendicular to the line which make angle 60° with x-axis.
along an perpendicular to the line which make angle 60° with x-axis.
Sol.

so the component along line = |Ay cos 30° + Ax cos 60°| and perpendicular to line = |Ax sin 60° - Ay sin 30°|
Ex.8 Resolve a weight of 10 N in two directions which are parallel and perpendicular to a slope inclined at 30° to the horizontal
Sol. Component perpendicular to the plane


=  =
=  N
N
and component parallel to the plane
W|| =W sin 30° = (10)  = 5 N
= 5 N
Ex.9 Resolve horizontally and vertically a force F = 8 N which makes an angle of 45° with the horizontal.
Sol. Horizontal component of is
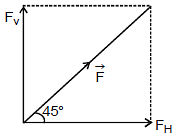
FH = F cos 45° = (8)  =
= 
and vertical component of is
Fv = F sin 45° =  =
=  Ans.
Ans.
Procedure to solve the Vector Equation
 ...(1)
...(1)
(a) There are 6 variables in this equation which are the following :
(1) Magnitude of  and its direction
and its direction
(2) Magnitude of  and its direction
and its direction
(3) Magnitude of  and its direction.
and its direction.
(b) We can solve this equation if we know the value of 4 variables [Note : two of them must be directions]
(c) If we know the two direction of any two vectors then we will put them on the same side and other on the different side.
For example
If we know the directions of  and and
and and  direction is unknown then we make equation as follows:-
direction is unknown then we make equation as follows:-
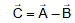
(d) Then we make vector diagram according to the equation and resolve the vectors to know the unknown values.
Ex.10 Find the net displacement of a particle from its starting point if it undergoes two successive displacements given by  , 37° North of West,
, 37° North of West,  , 53° North of East
, 53° North of East
Sol. 



Angle from west - east axis (x - axis)
Ex.11 Find magnitude of  and direction of
and direction of  . If
. If  makes angle 37° and
makes angle 37° and  makes 53° with x axis and
makes 53° with x axis and  has magnitude equal to 10 and
has magnitude equal to 10 and  has 5. (given
has 5. (given  )
)
Sol.



B = 5 (magnitude can not be negative) & Angle made by A
Ex.12 Find the magnitude of F1 and F2. If F1, F2 make angle 30° and 45° with F3 and magnitude of F3 is 10 N. (given  =
=  )
)
Sol.


Short Method

If their are two vectors  and their resultant make an angle α with
and their resultant make an angle α with  . then A sin α = β sin β
. then A sin α = β sin β
Means component of  perpendicular to resultant is equal in magnitude to the component of
perpendicular to resultant is equal in magnitude to the component of  perpendicular to resultant.
perpendicular to resultant.
Ex.13 If two vectors  and
and  make angle 30° and 45° with their resultant and
make angle 30° and 45° with their resultant and  has magnitude equal to 10, then find magnitude of
has magnitude equal to 10, then find magnitude of  .
.
Sol. B sin 60° = A sin 30°
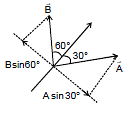
⇒ 10 sin 60° = A sin 30°
⇒ A = 
Ex.14 If  and
and  have angle between them equals to 60° and their resultant make, angle 45° with
have angle between them equals to 60° and their resultant make, angle 45° with  and
and  have magnitude equal to 10. Then Find magnitude of
have magnitude equal to 10. Then Find magnitude of  .
.
Sol. here a = 45° and b = 60° -45° = 15°
so A sinα = B sinβ
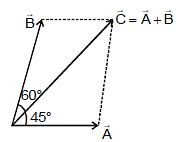
10 sin 45° = B sin 45°
So B = 
= 
Addition and Subtraction in Component Form
Suppose there are two vectors in component form. Then the addition and subtraction between these two are



Also if we are having a third vector present in component form and this vector is added or subtracted from the addition or subtraction of above two vectors then


Note : Modulus of vector A is given by

Ex.15 Obtain the magnitude of  if
if
 and
and 
Sol. 
 Magnitude of
Magnitude of 
=  Ans.
Ans.
Ex.16 Find  and
and  if
if  make angle 37° with positive x-axis and
make angle 37° with positive x-axis and  make angle 53° with negative x-axis as shown and magnitude of
make angle 53° with negative x-axis as shown and magnitude of  is 5 and of B is 10.
is 5 and of B is 10.
Sol. 
for 
 +
+  =
= 
so the magnitude of resultant will be =  =
= 
and have angle θ =  from negative x - axis towards up
from negative x - axis towards up
for 

So the magnitude of resultant will be
= 
and have angle  from positive x-axis towards down.
from positive x-axis towards down.
Multiplication of Vectors (The Scalar and vector products)
Scalar Product
The scalar product or dot product of any two vectors  and
and  , denoted as
, denoted as  .
.  (read
(read  dot
dot  ) is defined as the product of their magnitude with cosine of angle between them.
) is defined as the product of their magnitude with cosine of angle between them.
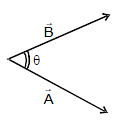
Thus,
 (here θ is the angle between the vectors)
(here θ is the angle between the vectors)
Properties :
- It is always a scalar which is positive if angle between the vectors is acute (i.e.< 90°) and negative if angle between them is obtuse (i.e., 90° < q £ 180°)
- It is commutative i.e.

- It is distributive, i.e.

- As by definition
 .
. = AB cosθ . The angle between the vectors θ =
= AB cosθ . The angle between the vectors θ = 

Geometrically, B cosθ is the projection of  onto
onto  and vice versa
and vice versa


Component of  along
along  = B cosθ =
= B cosθ =  =
=  (Projection of
(Projection of  on
on  )
)
Component of  along
along  = A cosθ =
= A cosθ =  =
=  (Projection of
(Projection of  on
on  )
)
- Scalar product of two vectors will be maximum when cosθ = max = 1, i.e., θ = 0°,
i.e., vectors are parallel ⇒ 
- If the scalar product of two non-zero vectors vanishes then the vectors are perpendicular.
- The scalar product of a vector by itself is termed as self dot product and is given by
 = AA cosθ = A2 ⇒
= AA cosθ = A2 ⇒ 
- In case of unit vector
 ,
, 

In case of orthogonal unit vectors,


Ex.17 If the vectors  and
and  are perpendicular to each other. Find the value of a?
are perpendicular to each other. Find the value of a?
Sol. If vectors  and
and  are perpendicular
are perpendicular
⇒  ⇒
⇒ 
⇒ a2 -2a -3 = 0 ⇒ a2 -3a a -3 = 0
⇒ a(a -3) +1 (a -3 ) ⇒ a = -1, 3
Ex.18 Find the component of  along
along  ?
?
Sol. Component of  along
along  is given by
is given by  hence required component
hence required component
= 
Ex.19 Find angle between  and
and  ?
?
Sol. We have cosθ = 
cosθ =  =
=  θ = cos-1
θ = cos-1
Ex.20 (i) For what value of m the vector  is perpendicular to
is perpendicular to 
(ii) Find the component of vector  along the direction of
along the direction of  ?
?
Sol. 
(i) m = -10 (ii) 
Important Note :
Components of b along and perpendicular to a.
Let  .
.  represent two (non-zero) given vectors a, b respectively. Draw BM perpendicular to
represent two (non-zero) given vectors a, b respectively. Draw BM perpendicular to 
From ΔOMB,  =
= 


Thus  are components of b along a and perpendicular to a.
are components of b along a and perpendicular to a.
Now


Hence, components of b along a perpendicular to a are.
(a . b/ |a|2) a and b - (a . b / |a|2) a respectively.
Ex.21 The velocity of a particle is given by  . Find the vector component of its velocity parallel to the line
. Find the vector component of its velocity parallel to the line  .
.
Sol. Component of  along
along 




Vector Product
The vector product or cross product of any two vectors and  , denoted as
, denoted as
 (read
(read  cross
cross  ) is defined as :
) is defined as :

Here θ is the angle between the vectors and the direction  is given by the right - hand - thumb rule.
is given by the right - hand - thumb rule.
Right - Hand - Thumb Rule :
To find the direction of  , draw the two vectors
, draw the two vectors  and
and  with both the tails coinciding. Now place your stretched right palm perpendicular to the plane of
with both the tails coinciding. Now place your stretched right palm perpendicular to the plane of  and
and  in such a way that the fingers are along the vector
in such a way that the fingers are along the vector  and when the fingers are closed they go towards
and when the fingers are closed they go towards  . The direction of the thumb gives the direction of
. The direction of the thumb gives the direction of  .
.

Properties :
- Vector product of two vectors is always a vector perpendicular to the plane containing the two vectors i.e. orthogonal to both the vectors and , though the vectors and
 may or may not be orthogonal.
may or may not be orthogonal. - Vector product of two vectors is not commutative i.e.
 But
But 
- The vector product is distributive when the order of the vectors is strictly maintained i.e.

- The magnitude of vector product of two vectors will be maximum when sinθ = max = 1. i.e. θ = 90°

- The magnitude of vector product of two non-zero vectors will be minimum when |sinθ| = minimum = 0, i.e., θ = 0° or 180° and
 i.e., if the vector product of two non-zero vectors vanishes, the vectors are collinear.
i.e., if the vector product of two non-zero vectors vanishes, the vectors are collinear. - The self cross product i.e. product of a vector by itself vanishes i.e. is a null vector.

- In case of unit vector
 ,
,  ⇒
⇒ 
- In case of orthogonal unit vectors
 and
and  in accordance with right-hand-thumb-rule,
in accordance with right-hand-thumb-rule,
- In terms of components.


Ex.22  is East wards and
is East wards and  is downwards. Find the direction of
is downwards. Find the direction of  ×
×  ?
?
Sol. Applying right hand thumb rule we find that  is along North.
is along North.
Ex.23 If  , find angle between
, find angle between  and
and 
Sol.  AB cosθ = AB sinθ tanθ = 1 ⇒ θ = 45°
AB cosθ = AB sinθ tanθ = 1 ⇒ θ = 45°
Ex.24  ⇒
⇒  here
here  is perpendicular to both
is perpendicular to both  and
and 
Ex.25 Find  if
if  and
and 
Sol.  =
=  =
= 
Ex.26 (i)  is North-East and
is North-East and  is down wards, find the direction of
is down wards, find the direction of 
(ii) Find  ×
×  if
if  and
and 
Ans. (i) North - West. (ii) 
Position and Displacement Vector
- Position vector for a point is vector for which tail is origin & head is the given point itself.
- Position vector of a point defines the position of the point w.r.t. the origin.




Change in position vector of particle is known as displacement vector.

Thus we can represent a vector in space starting from (x , yj & ending at

CALCULUS
14. Constants : They are fixed real number which value does not change
Ex. 3, e, a, -1, etc.
15. Variable :
Something that is likely to vary, something that is subject to variation.
or
A quantity that can assume any of a set of value.
Types of variables.
(i) Independent variables : Independent variables is typically the variable being manipulated or changed
(ii) dependent variables : The dependent variables is the object result of the independent variable being manipulated.
Ex. y = x2
here y is dependent variable and x is independent variable
16. FUNCTION :
Function is a rule of relationship between two variables in which one is assumed to be dependent and the other independent variable.
The temperatures at which water boils depends on the elevation above sea level (the boiling point drops as you ascend). Here elevation above sea level is the independent & temperature is the dependent variable.
The interest paid on a cash investment depends on the length of time the investment is held. Here time is the independent and interest is the dependent variable.
In each case, the value of one variable quantity (dependent variable), which we might call y, depends on the value of another variable quantity (independent variable), which we might call x. Since the value of y is completely determined by the value of x, we say that y is a function of x and represent it mathematically as y = f(x).

all possible values of independent variables (x) are called domain of function.
all possible values of dependent variable (y) are called Range of function.
Think of function f as a kind machine that produces an output value f(x) in its range whenever we feed it an input value x from its domain (figure).
When we study circles, we usually call the area A and the radius r. Since area depends on radius, we say that A is a function of r, A = f(r). The equation A = πr2 is a rule that tells how to calculate a unique (single) output value of A for each possible input value of the radius r.
A = f(x) = πr2. (Here the rule of relationship which describes the function may be described as square & multiply by π)
if r = 1 A = π
if r = 2 A = 4π
if r = 3 A = 9π
The set of all possible input values for the radius is called the domain of the function. The set of all output values of the area is the range of the function.
We usually denote functions in one of the two ways :
1. By giving a formula such as y = x2 that uses a dependent variable y to denote the value of the function.
2. By giving a formula such as f(x) =x2 that defines a functions symbols f to name the function.
Strictly speaking, we should call the function f and not f(x).
y = sin x. Here the function is y since, x is the independent variable.
Ex.27 The volume V of ball (solid sphere) of radius r is given by the function V(r) = 
The volume of a ball of radius 3m is?
Sol. V(3) =  = 36 pm3.
= 36 pm3.
Ex.28 Suppose that the function F is defined for all real numbers r by the formula.
F(r) = 2 (r -1) +3.
Evaluate F at the input values 0, 2 x 2, and F(2).
Sol. In each case we substitute the given input value for r into the formula for F:
F(0) = 2(0 -1) + 3 = -2 + 3 = 1
F(2) = 2(2 -1) + 3 = 2 + 3 =5
F(x + 2) = 2 (x + 2 -1) + 3 = 2x + 5
F(F(2)) = F(5) = 2(5 -1) 3 = 11
Ex. 29 function f(x) is defined as f(x) = x2 + 3, Find f(0), f(l), f(x>), f(x + 1) and f(f(l))
Sol. f(0) = 02 + 3 = 3
f(1) = l2 + 3 = 4
f(x2) = (x2)2 +3 = x4 + 4
f(x +1) = (x + 1)2 + 3 = x2 + 2x + 4
= f(4) = 42+3 = 19
17. Differentiation
Finite difference :
The finite difference between two values of a physical is represented by Δ notation.
For example :
Difference in two values of y is written as Δy as given in the table below.
y2 | 100 | 100 | 100 |
y1 | 50 | 99 | 99.5 |
Δy = y2 - y1 | 50 | 1 | 0.5 |
Infinitely small difference :
The infinitely small difference means very-very small difference. And this difference is represented by 'd' notation instead of 'D'.
For example infinitely small difference in the values of y is written as 'dy'
if y2 = 100 and y1 = 99.9999999999999.....
then dy = 0.00000000000000..........00001
Definition of differentiation
Another name of differentiation is derivative. Suppose y is a function of x or y = f(x)
Differentiation of y with respect to x is denoted by symbols f' (x)
where f'(x) =  ; dx is very small change in x and dy is corresponding very small change in y.
; dx is very small change in x and dy is corresponding very small change in y.
Notation : There are many ways to denote the derivative of function y = f(x), the most common notations are these :
y | "y prime" | Nice and brief and does not name the independent variable |
dy/dx | " dy by dx" | Names the variables and uses d for derisive |
df/dx | " df by dx" | Emphasizes the function's name |
| ” d by dx of f" | Emphasizes the idea that differentiation is an operation performed on f. |
Dxf | " dx of f" | A common operator notation |
| ” y dot" | One of Newton's notations, now common for time derivative i.e. dy/dt |
Average rates of change :
Given an arbitrary function y = f(x) we calculate the average rate of change of y with respect to x over the interval (x, x +Δx) by dividing the change in value of y, i.e., Dy = f(x+Δx) -f(x), by length of interval Δx over which the change occurred.
The average rate of change of y with respect to x over the interval [x, x+Δx]


Geometrically
 = tanθ = Slope of the line PQ
= tanθ = Slope of the line PQ
In triangle QPR tanθ = 
therefore we can say that average rate of change of y with respect to x is equal to slope of the line joining P & Q.
The derivative of a function
We know that Average rate of change of y w.r.t x is -

If the limit of this ratio exists as Δx → 0, then it is called the derivative of given function f(x) and is denoted as

18. GEOMETRICAL MEANING OF DIFFERENTIATION :
The geometrical meaning of differentiation is very much useful in the analysis of graphs in physics. To understand the geometrical meaning of derivatives we should have knowledge of secant and tangent to a curve.
Secant and Tangent to a Curve
Secant : - A secant to a curve is a straight line, which intersects the curve at any two points.

Tangent :
A tangent is a straight line, which touches the curve a particular point. Tangent is limiting case of secant which intersects the curve at two overlapping points.
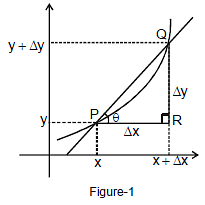
In the figure - 1 shown, if value of Δx has gradually reduced then the point Q will move nearer to the point P. If the process is continuously repeated (Figure-2) value of Δx will be infinitely small and secant PQ to the given curve will become a tangent at point P.
Therefore

we can say that differentiation of y with respect to x, i.e.  is equal to slope of the tangent at point P (x,y)
is equal to slope of the tangent at point P (x,y)
or tanθ = 
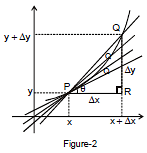
(From fig-1 the average rate change of y from x to x+Δx is identical with the slope of secant PQ)
Rule No. 1 Derivative Of A Constant
The first rule of differentiation is that the derivative of every constant function is zero.
If c is constant, then 
Ex.30 ,
,  ,
, 
Rule No.2 Power Rule
If n is a real number, then 
To apply the power Rule, we subtract 1 from the original exponent (n) and multiply the result by n.
Ex.31



Function defined for x > 0 derivative defined only for x > 0

Function defined for x > 0 derivative not defined at x = 0
Rule No.3 The Constant Multiple Rule
If u is a differentiable function of x, and c is a constant, then 
In particular, if n is a positive integer, then 
Ex.34 The derivative formula

says that if we rescale the graph of y = x2 by multiplying each y-coordinate by 3, then we multiply the slope at each point by 3.
Ex.35 A useful special case
The derivative of the negative of a differentiable function is the negative of the function's derivative. Rule 3 with c = -1 gives.

Rule No.4 The Sum Rule
The derivative of the sum of two differentiable functions is the sum of their derivatives.
If u and v are differentiable functions of x, then their sum u+v is differentiable at every point where u and v are both differentiable functions in their derivatives.

The sum Rule also extends to sums of more than two functions, as long as there are only finite functions in the sum. If u1, u2, ........ un is differentiable at x, then so if u1+u2 ....... +un, then



Notice that we can differentiate any polynomial term by term, the way we differentiated the polynomials in above example.
Rule No. 5 The Product Rule
If u and v are differentiable at x, then if their product uv is considered, then  .
.
The derivative of the product uv is u times the derivative of v plus v times the derivative of u. In prime notation
(uv)' = uv' + vu'.
While the derivative of the sum of two functions is the sum of their derivatives, the derivative of the product of two functions is not the product of their derivatives. For instance,
 while
while  , which is wrong
, which is wrong
Ex.37 Find the derivatives of y = (x2+1) (x3+3)
Sol. Using the product Rule with u = x2+1 and v = x3+3, we find
 = (x2+1) (3x2) + (x3+3) (2x)
= (x2+1) (3x2) + (x3+3) (2x)
= 3x4 + 3x2 + 2x4 + 6x = 5x4 + 3x2 + 6x
Example can be done as well (perhaps better) by multiplying out the original expression for y and differentiating the resulting polynomial. We now check :
y = (x2 + 1) (x3 + 3) = x5 + x3 + 3x2 + 3
 = 5x4 + 3x2 + 6x
= 5x4 + 3x2 + 6x
This is in agreement with our first calculation.
There are times, however, when the product Rule must be used. In the following examples. We have only numerical values to work with.
Ex.38 Let y = uv be the product of the functions u and v. Find y'(2) if u(2) = 3, u'(2) = -4, v(2) = 1, and v'(2) = 2.
Sol.
From the Product Rule, in the form y' = (uv)' = uv' + vu',
we have y'(2) = u(2) v'(2) + v(2) u'(2)
= (3) (2) + (1) (-4) = 6-4 = 2
Rule No.6 The Quotient Rule
If u and v are differentiable at x, and v(x) ¹ 0, then the quotient u/v is differentiable at x,
and 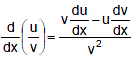
Just as the derivative of the product of two differentiable functions is not the product of their derivatives, the derivative of the quotient of two functions is not the quotient of their derivatives.
Ex.39 Find the derivative of 
Sol. We apply the Quotient Rule with u = t2 -1 and v = t2 1




Rule No. 7 Derivative Of Sine Function

Ex.40 






Rules No.8 Derivative Of Cosine Function

Ex.41 (a) y = 5x + cos x Sum Rule
 Product Rule
Product Rule
= sin x(— sin x) + cos x (cos x)
= cos2 x - sin2 x - cos 2x
Rule No. 9 Derivatives Of Other Trigonometric Functions
Because sin x and cos x are differentiable functions of x, the related functions
 ;
; 
 ;
; 
are differentiable at every value of x at which they are defined. There derivatives, Calculated from the Quotient Rule, are given by the following formulas.
 ;
; 
 ;
; 
Ex.42 Find dy / dx if y = tan x.
Sol.


Ex. 43 
Rule No. 10 Derivative Of Logarithm And Exponential Functions
 ,
, 
Ex.44 y = ex . loge (x)
 ⇒
⇒ 
Rule No. 11 Chain Rule Or `Outside Inside' Rule

It sometimes helps to think about the Chain Rule the following way. If y = f(g(x)),
 = f'[g(x)] . g'(x)
= f'[g(x)] . g'(x)
In words : To find dy/dx, differentiate the "outside" function f and leave the "inside" g(x) alone; then multiply by the derivative of the inside.
We now know how to differentiate sin x and x2 -4, but how do we differentiate a composite like sin(x2 -4)?
The answer is, with the Chain Rule, which says that the derivative of the composite of two differentiable functions is the product of their derivatives evaluated at appropriate points. The Chain Rule is probably the most widely used differentiation rule in mathematics. This section describes the rule and how to use it. We begin with examples.
Ex.45 The function y = 6x -10 = 2(3x -5) is the composite of the functions y = 2u and u = 3x -5. How are the derivatives of these three functions related ?
Sol. We have  ,
,  ,
, 
Since 6 = 2 × 3 
Is it an accident that  ?
?
If we think of the derivative as a rate of change, our intuitions allows us to see that this relationship is reasonable. For y = f(u) and u = g(x), if y changes twice as fast as u and u changes three times as fast as x, then we expect y to change six times as fast as x.
Ex.46 Let us try this again on another function.
y = 9x4 +6x2 +1 = (3x2 +1)2
is the composite y = u2 and u = 3x2 + 1. Calculating derivatives. We see that
 = 2 (3x2 + 1). 6x = 36x3 + 12 x
= 2 (3x2 + 1). 6x = 36x3 + 12 x
and  = 36 x3 + 12 x
= 36 x3 + 12 x
Once again, 
The derivative of the composite function f(g(x)) at x is the derivative of f at g(x) times the derivative of g at x.
Ex.47 Find the derivation of 
Sol. Here y = f(g(x)), where f(u) =  and u = g(x) = x2 + 1. Since the derivatives of f and g are
and u = g(x) = x2 + 1. Since the derivatives of f and g are
f' (u) =  and g'(x) = 2x,
and g'(x) = 2x,
the Chain Rule gives
 = f' (g(x)).g'(x) =
= f' (g(x)).g'(x) =  .g'(x) =
.g'(x) =  . (2x) =
. (2x) = 
Ex.48


Ex. 49  u = 1 - x2 and n = 1/4
u = 1 - x2 and n = 1/4
(Function defined) on [-1, 1]




Rule No. 12 Power Chain Rule
* If 
Ex.50  =
=  = -1 (3x -2)-2
= -1 (3x -2)-2
= -1 (3x -2)-2 (3) = -
In part (d) we could also have found the derivation with the Quotient Rule.
Ex.51 (a)
Sol. Here u = Ax B, 
(b)
(c) log(Ax B) =
log(Ax B) =  .A
.A
(d) tan (Ax + B) = sec2 (Ax + B).A
tan (Ax + B) = sec2 (Ax + B).A
(e)
Note : These results are important
19. DOUBLE DIFFERENTIATION
If f is differentiable function, then its derivative f' is also a function, so f' may have a derivative of its own, denoted by  . This new function f'' is called the second derivative of because it is the derivative of the derivative of f. Using Leibniz notation, we write the second derivative of y = f(x) as
. This new function f'' is called the second derivative of because it is the derivative of the derivative of f. Using Leibniz notation, we write the second derivative of y = f(x) as

Another notation is f''(x) = D2 f(x).
Ex.52 If(x) = x cos x, find f'' (x)
Sol. Using the Product Rule, we have f'(x) 
To find f" (x) we differentiate f'(x)


= - x cos x - sinx - sinx = - x cos x - 2 sin x
20. Application of derivative Differentiation as a rate of change
 is rate of change of 'y' with respect to 'x' :
is rate of change of 'y' with respect to 'x' :
For examples :
(i) v =  this means velocity 'v' is rate of change of displacement 'x' with respect to time 't'
this means velocity 'v' is rate of change of displacement 'x' with respect to time 't'
(ii) a =  this means acceleration 'a' is rate of change of velocity 'v' with respect to time 't'.
this means acceleration 'a' is rate of change of velocity 'v' with respect to time 't'.
(iii)  this means force 'F' is rate of change of momentum 'p' with respect to time 't'.
this means force 'F' is rate of change of momentum 'p' with respect to time 't'.
(iv) 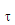 =
=  this means torque 't' is rate of change of angular momentum 'L' with respect to time 't'
this means torque 't' is rate of change of angular momentum 'L' with respect to time 't'
(v) Power =  this means power 'P' is rate of change of work 'W' with respect to time 't'
this means power 'P' is rate of change of work 'W' with respect to time 't'
Ex.53 The area A of a circle is related to its diameter by the equation  .
.
How fast is the area changing with respect to the diameter when the diameter is 10 m ?
Sol. The (instantaneous) rate of change of the area with respect to the diameter is

When D =10m, the area is changing at rate (π/2) = 5π m2/m. This means that a small change ΔD m in the diameter would result in a change of about 5p ΔD m2 in the area of the circle.
Physical Example :
Ex.54 Boyle's Law states that when a sample of gas is compressed at a constant temperature, the product of the pressure and the volume remains constant : PV = C. Find the rate of change of volume with respect to pressure.
Sol. 
Ex.55 (a) Find the average rate of change of the area of a circle with respect to its radius r as r changed from
(i) 2 to 3 (ii) 2 to 2.5 (iii) 2 to 2.1
(b) Find the instantaneous rate of change when r = 2.
(c) Show that there rate of change of the area of a circle with respect to its radius (at any r) is equal to the circumference of the circle. Try to explain geometrically when this is true by drawing a circle whose radius is increased by an amount Δr. How can you approximate the resulting change in area ΔA if Δr is small ?
Sol. (a) (i) 5π (ii) 4.5 π (iii) 4.1 π
(b) 4π
(c) ΔA ≈ 2 πrΔr
21. MAXIMA & MINIMA
Suppose a quantity y depends on another quantity x in a manner shown in figure. It becomes maximum at x1 and minimum at x2. At these points the tangent to the curve is parallel to the x-axis and hence its slope is tanθ = 0. Thus, at a maximum or a minima slope
⇒ 
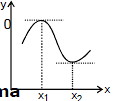
Maxima
Just before the maximum the slope is positive, at the maximum it is zero and just after the maximum it is negative. Thus,  decrease at a maximum and hence the rate of change of
decrease at a maximum and hence the rate of change of  is negative at a maximum i.e.,
is negative at a maximum i.e.,  at maximum. The quantity
at maximum. The quantity  is the rate of change of the slope. It is written as
is the rate of change of the slope. It is written as  . Conditions for maxima are : (a)
. Conditions for maxima are : (a)  (b)
(b) 
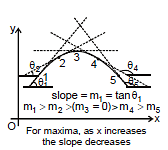
Minima
Similarly, at a minimum the slope changes from negative to positive, Hence with the increases of x. The slope is increasing that means the rate of change of slope with respect to x is positive.
Hence 
Conditions for minima are :
(a)  (b)
(b) 
Quite often it is known from the physical situation whether the quantity is a maximum or a minimum. The test on  may then be omitted.
may then be omitted.
Ex.56 Find maximum or minimum values of the functions :
(A) y = 25x2 + 5 -10x (B) y = 9 -(x -3)2
Sol. (A) For maximum and minimum value, we can put 
or 
 x =
x = 
Further, 
or  has positive value at x =
has positive value at x =  . Therefore, y has minimum value at x =
. Therefore, y has minimum value at x =  . Therefore, y has minimum value at x =
. Therefore, y has minimum value at x = 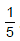 . Substituting x =
. Substituting x =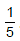 in given equation, we get
in given equation, we get
ymin = 
(B) y = 9 -(x -3)2 = 9 -x2 +-9 6x
or y = 6x -x2

For minimum or maximum value of y we will substitute 
or 6 -2x = 0
x = 3
To check whether value of y is maximum or minimum at x = 3 we will have to check whether  is positive or negative.
is positive or negative.

or  is negative at x = 3. Hence, value of y is maximum. This maximum value of y is,
is negative at x = 3. Hence, value of y is maximum. This maximum value of y is,
ymax = 9 -(3 -3)2 = 9
22. INTEGRATION
Definitions :
A function F(x) is a antiderivative of a function f(x) if
F'(x) = f(x)
for all x in the domain of f. The set of all antiderivatives of f is the indefinite integral of f with respect to x, denoted by
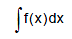
The symbol  is an integral sign. The function f is the integrand of the integral and x is the variable of integration.
is an integral sign. The function f is the integrand of the integral and x is the variable of integration.
For example f(x) = x3 then f'(x) = 3x2
So the integral of 3x2 is x3
Similarly if f(x) = x3 + 4
there for the general integral of 3x2 is x3 + c where c is a constant
One antiderivative F of a function f, the other antiderivatives of f differ from F by a constant. We indicate this in integral notation in the following way :
 .....(i)
.....(i)
The constant C is the constant of integration or arbitrary constant, Equation (1) is read, "The indefinite integral of f with respect to x is F(x) + C." When we find F(x) + C, we say that we have integrated f and evaluated the integral.
Ex.57 Evaluate 
Sol.
The formula x2 + C generates all the antiderivatives of the function 2x. The function x2+ 1, x2 -π, and
x2+ are all antiderivatives of the function 2x, as you can check by differentiation.
are all antiderivatives of the function 2x, as you can check by differentiation.
Many of the indefinite integrals needed in scientific work are found by reversing derivative formulas.
Integral Formulas
| Indefinite Integral | Reversed derivated formula |
1.
|
|
2.  |  |
3.  |  |
4.  |  |
5.  | 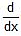 (-cot x) = cosec2 x (-cot x) = cosec2 x |
6.  |  = sec x tan x = sec x tan x |
7.  = -cosec x +C = -cosec x +C | 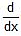 (-cosec x) = cosec x cot x (-cosec x) = cosec x cot x |
Ex.58 Examples based on above formulas :
(a) 
(b)  Formula 1 with n = 5
Formula 1 with n = 5
(c)  Formula 1 with n =
Formula 1 with n = 
(d)  Formula 2 with k = 2
Formula 2 with k = 2
(e)  =
=  =
=  Formula 3 with k =
Formula 3 with k = 
Ex.59 Right : = x sin x + cos x C
= x sin x + cos x C
Reason : The derivative of the right-hand side is the integrand :
Check :  = x cos x + sin x -sin x + 0 = x cos x.
= x cos x + sin x -sin x + 0 = x cos x.
Wrong : = x sin x +C
= x sin x +C
Reason : The derivative of the right-hand side is not the integrand :
Check : = x cos x + sin x + 0
= x cos x + sin x + 0 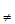 x cos x
x cos x
Rule No. 1 Constant Multiple Rule
- A function is an anti derivative of a constant multiple k of a function f if and only if it is k times an antiderivative of f.

Ex.60  =
=  =
= 
Rule No.2 Sum And Difference Rule
- A function is an anti derivative of a sum or difference f ± g if and only if it is the sum or difference of an anti derivative of f an anti derivative of g.

Ex.61 Term-by-term integration
Evaluate : 
Sol. If we recognize that (x3/3) -x2 +5x is an anti derivative of x2 -2x +5, we can evaluate the integral as

If we do not recognize the anti derivative right away, we can generate it term by term with the sum and difference Rule :


This formula is more complicated than it needs to be. If we combine C1, C2 and C3 into a single constant
C = C1 + C2 + C3, the formula simplifies to

and still gives all the anti derivatives there are. For this reason we recommend that you go right to the final form even if you elect to integrate term by term. Write
Find the simplest anti derivative you can for each part add the constant at the end.
Ex.62 We can sometimes use trigonometric identities to transform integrals we do not know how to evaluate into integrals. The integral formulas for sin2 x and cos2 x arise frequently in applications.
(a)  =
= 

= 

(b)  =
= 

 As in part (a), but with a sign change
As in part (a), but with a sign change
23. Some Indefinite integrals (An arbitrary constant should be added to each of these integrals.
(a)  (provided n ¹ --1) C
(provided n ¹ --1) C
(b) 
(c) 
(d) 
(e) 
(f)
Ex.63 (a) 
(b)
(c) 
(d)
(e) 
(f) 
(g) 
(h) 
24. DEFINITE INTEGRATION OR INTEGRATION WITH LIMITS


Ex.64  = 3 [4 -(-1)] = (3) (5) = 15
= 3 [4 -(-1)] = (3) (5) = 15
 =
=  + cos (0) = -0 + 1 = 1
+ cos (0) = -0 + 1 = 1
Ex.65 (1) 
(2) 
(3) 
25. APPLICATION OF DEFINITE INTEGRAL
Calculation Of Area Of A Curve.

From graph shown in figure if we divide whole area in infinitely small strips of dx width.
We take a strip at x position of dx width.
Small area of this strip dA = f(x) dx
So, the total area between the curve and x-axis = sum of area of all strips = 
Let f(x) > 0 be continuous on [a,b]. The area of the region between the graph of f and the x-axis is

Ex.66 Using an area to evaluate a definite integral
Evaluate  0 < a < b.
0 < a < b.
Sol. We sketch the region under the curve y = x, a £ x £ b (figure) and see that it is a trapezoid with height (b -a) and bases a and b.

The value of the integral is the area of this trapezoid :
Thus =

and so on.
Notice that x2/2 is an antiderivative of x, further evidence of a connection between antiderivatives and summation.
(i) To find impulse
 so implies =
so implies = 
Ex.67 If F = kt then find impulse at t = 3 sec.
so impulse will be area under f - t curve
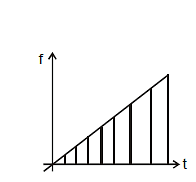
 =
= 
⇒ 
2. To calculate work done by force :


So area under f - x curve will give the value of work done.
|
97 videos|378 docs|103 tests
|
FAQs on Resolution of Vectors: Motion in a Plane - Physics Class 11 - NEET
| 1. What is the importance of resolving vectors in motion in a plane? |  |
| 2. How do we resolve vectors in motion in a plane? |  |
| 3. Can resolving vectors in motion in a plane help in predicting the path of an object? |  |
| 4. What are some common applications of resolving vectors in motion in a plane? |  |
| 5. How does resolving vectors in motion in a plane help in determining the velocity and acceleration of an object? |  |

|
Explore Courses for NEET exam
|

|