Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Circle: Arc and Cyclic Properties
Revision Notes: Circle: Arc and Cyclic Properties | Mathematics Class 10 ICSE PDF Download
Some terms associated with circle
- Circles having the same centre but with different radii are said to be concentric circles.
- Two circles are said to be equal or congruent if they have equal radii.
- A circle passing through all the vertices of a polygon is called circumscribed circle of the polygon and its centre is called circumcentre.
The polygon is called inscribed polygon. - A circle touching all the sides of a polygon is called an inscribed circle of the polygon and its centre is called incentre.
- The line segment joining any two points on the circumference of the circle is called a chord of the circle.
- A chord of a circle passing through its centre is called a diameter of the circle
- A straight line drawn from the centre of a circle to bisect a chord which is not a diameter is at right angles to chord.
- Perpendicular drawn to a chord from the centre of a circle bisects the chord.
- One and only one circle passes through three given points not in a straight line.
- Equal chords are equidistant from centre.
- Chords which are equidistant from the centre are equal in lengths.
Arc
An arc is a part of the circumference of a circle.
An arc less than one-half of the whole arc of a circle is called a minor arc of the circle, and an arc greater than one-half of the whole arc of a circle is called a major arc of the circle.
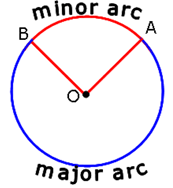
The whole arc of a circle is called the circumference of the circle.
One-half of the whole arc of a circle is called a semi-circle of the circle.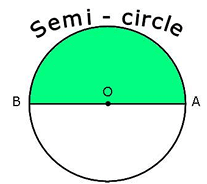
Segment of a Circle
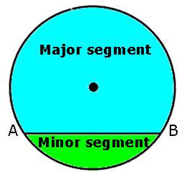
A chord of a circle divides it into two parts. Each part is called a segment.
The part containing the minor arc is called the minor segment, and the part containing the major arc is called the major segment.
Relation between Arcs and Segments
The angle which, an arc of a circle subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.
Angles in the same segment of a circle are equal.
The angle in a semi-circle is a right angle.
Cyclic Properties
A quadrilateral inscribed in a circle is called a cyclic quadrilateral.
The opposite angles of a cyclic quadrilateral are supplementary.
If a pair of opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
The document Revision Notes: Circle: Arc and Cyclic Properties | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|198 docs|30 tests
|
FAQs on Revision Notes: Circle: Arc and Cyclic Properties - Mathematics Class 10 ICSE
| 1. What is the definition of an arc in a circle? |  |
Ans. An arc is a portion of the circumference of a circle. It is defined by two points on the circle and is measured in degrees or radians. The arc can be classified as a minor arc (less than 180 degrees) or a major arc (more than 180 degrees).
| 2. How do cyclic properties relate to angles in a circle? |  |
Ans. Cyclic properties refer to the relationships between angles in a circle, especially in cyclic quadrilaterals. For instance, in a cyclic quadrilateral, the sum of the opposite angles is always 180 degrees. This property helps in solving various problems related to angles and arcs in circles.
| 3. What is the relationship between the length of an arc and the radius of the circle? |  |
Ans. The length of an arc (L) can be calculated using the formula L = (θ/360) × 2πr, where θ is the central angle in degrees and r is the radius of the circle. This shows that the length of an arc is directly proportional to both the radius of the circle and the measure of the angle subtended at the center.
| 4. Can you explain the concept of inscribed angles in a circle? |  |
Ans. An inscribed angle is formed by two chords in a circle that share an endpoint. The vertex of the angle is on the circle, and the sides of the angle are defined by the chords. The measure of an inscribed angle is always half the measure of the central angle that subtends the same arc.
| 5. What is the significance of cyclic quadrilaterals in geometry? |  |
Ans. Cyclic quadrilaterals are significant because they have special properties that simplify various geometric proofs and calculations. For example, in a cyclic quadrilateral, the opposite angles are supplementary, and the area can be calculated using Brahmagupta's formula. These properties are often used in problems involving circles and angles.
Related Searches















